Andres_Lionel
Andres_Lionel

牛妹的苹果树【牛客练习赛67 F】【倍增+欧拉序+树的直径】

题目链接

  求区间[l, r]内的点对的最大直径。

  其实，我们可以发现直径有相对应的传递关系的，如果我们已知一棵树上的直径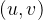，(u, v)，假设又知道另一棵树上的直径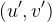，(u', v')，那么新的直径只能通过这四个点两两组和来实现的。

  所以，我们可以用倍增的方法来维护这个连续关系对。

9 1
1 2 1
1 3 2
1 4 3
1 5 5
1 6 6
2 7 7
3 8 4
4 9 2
6 7
ans:14

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 3e5 + 7;
int N, Q;
namespace Graph
{
    int head[maxN], cnt;
    struct Eddge
    {
        int nex, to; ll val;
        Eddge(int a=-1, int b=0, ll c=0):nex(a), to(b), val(c) {}
    } edge[maxN << 1];
    inline void addEddge(int u, int v, ll w)
    {
        edge[cnt] = Eddge(head[u], v, w);
        head[u] = cnt++;
    }
    inline void _add(int u, int v, ll w) { addEddge(u, v, w); addEddge(v, u, w); }
    inline void init()
    {
        cnt = 0;
        for(int i=1; i<=N; i++) head[i] = -1;
    }
};
using namespace Graph;
namespace Grand_Father
{
    int deep[maxN], euler[maxN << 1], Esiz, rid[maxN], LOG_2[maxN << 1];
    ll dis[maxN];
    void dfs(int u, int fa)
    {
        deep[u] = deep[fa] + 1; rid[u] = Esiz + 1;
        for(int i=head[u], v; ~i; i=edge[i].nex)
        {
            v = edge[i].to;
            if(v == fa) continue;
            euler[++Esiz] = u;
            dis[v] = dis[u] + edge[i].val;
            dfs(v, u);
        }
        euler[++Esiz] = u;
    }
    int mn[maxN << 1][20];
    inline void RMQ_Init()
    {
        for(int i=2; i<=(N << 1); i++) LOG_2[i] = LOG_2[i >> 1] + 1;
        dis[1] = 0;
        dfs(1, 0);
        for(int i=1; i<=Esiz; i++) mn[i][0] = euler[i];
        for(int j=1; (1 << j) <= Esiz; j++)
        {
            for(int i=1; i + (1 << j) - 1 <= Esiz; i++)
            {
                if(deep[mn[i][j - 1]] < deep[mn[i + (1 << (j - 1))][j - 1]]) mn[i][j] = mn[i][j - 1];
                else mn[i][j] = mn[i + (1 << (j - 1))][j - 1];
            }
        }
    }
    inline int Rmq(int l, int r)
    {
        int det = r - l + 1, kk = LOG_2[det];
        if(deep[mn[l][kk]] <= deep[mn[r - (1 << kk) + 1][kk]]) return mn[l][kk];
        else return mn[r - (1 << kk) + 1][kk];
    }
    inline int _LCA(int u, int v)
    {
        int l = rid[u], r = rid[v];
        if(l > r) swap(l, r);
        return Rmq(l, r);
    }
    inline ll _Dis(int u, int v)
    {
        int lca = _LCA(u, v);
        return dis[u] + dis[v] - 2 * dis[lca];
    }
};
using namespace Grand_Father;
#define MP(a, b) make_pair(a, b)
#define Max_3(a, b, c) max(a, max(b, c))
#define pii pair
pair ans[maxN][20];
bool cmp (pii e1, pii e2) { return _Dis(e1.first, e1.second) < _Dis(e2.first, e2.second); }
inline pii Big_one(pii x, pii y)
{
    pii ans;
    ans = max(x, y, cmp);
    ans = max(ans, MP(x.first, y.first), cmp);
    ans = max(ans, MP(x.first, y.second), cmp);
    ans = max(ans, MP(x.second, y.first), cmp);
    ans = max(ans, MP(x.second, y.second), cmp);
    return ans;
}
inline void Solve()
{
    for(int i=1; i<=N; i++) ans[i][0] = MP(i, i);
    pii a1, a2;
    for(int j=1; (1 << j) <= N; j++)
    {
        for(int i=1; i + (1 << j) - 1 <= N; i++)
        {
            a1 = ans[i][j - 1];
            a2 = ans[i + (1 << (j - 1))][j - 1];
            ans[i][j] = Big_one(a1, a2);
        }
    }
}
inline ll query(int l, int r)
{
    int det = r - l + 1, kk = LOG_2[det];
    pii s = Big_one(ans[l][kk], ans[r - (1 << kk) + 1][kk]);
    return _Dis(s.first, s.second);
}
int main()
{
    scanf("%d%d", &N, &Q);
    init();
    for(int i=1, u, v, w; i

 

你可能感兴趣的:(欧拉序,树的直径,欧拉序,倍增)

  • C语言代码练习（第十九天） 小小框架 C语言C语言重点练习c语言
    今日练习：52、有一个已经排好序的数组，要求输入一个数后，按原来排序的规律将它插入数组中53、输出"魔方阵"。所谓魔方阵是指它的每一行，每一列和对角线之和均相等。54、找出一个二维数组中的鞍点，即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点。有一个已经排好序的数组，要求输入一个数后，按原来排序的规律将它插入数组中运行代码intmain(){intarr[11]={1,3,9,12,15
  • 2021-01-09 哥伦比亚 《梦中的欢快葬礼和十二个异乡故事》 加西亚·马尔克斯 著 罗秀 译 juneyale
    《梦中的欢快葬礼和十二个异乡故事》哥伦比亚加西亚·马尔克斯著罗秀译序《总统先生，一路走好！》“再给我一杯咖啡。”他用纯正的法语说。随即补充道：“要意式咖啡，能让人起死回生的那种。”并没有意识到话里的双关含义。当火车开始加速，荷马突然发现总统的手杖还在自己手中，于是跑到站台尽头，把手杖用力扔过去，希望总统能在半空中接住。但是手杖掉在了铁轨上，随即被碾得粉碎。那真是恐怖的一瞬。拉萨拉看到的最后一幕是那
  • 2024春节微信红包封面序列号大全一览 帮忙赚赏金
    2024微信红包封面序列号哪里领取红包封面领取微信搜索公众号：【艺间封面】千万红包封面等你领取2024微信红包封面免费序列号如何设置微信红包封面？1.打开微信，点击好友选择红包。2.单击红包封面。3.单击“添加红包封面”。4.输入接收序列号。来一波免费的微信红包封面序列号微信红包封面序列号红包封面领取微信搜索公众号：艺间封面千万红包封面等你领取微信红包封面序列号kGnkrbw5a7N微信红包封面序
  • 2023-09-13 a6cad16c5cbf
    锅锅编故事序从小就喜欢海阔天空的锅锅，终于安份了。因为她有了小口。小口是个安静的孩子，锅锅为了自己的天马行空得以释放决定给口口讲故事。第一集口口总是喜欢盯着阳台的一小盆雏菊，眼神都不给锅锅一个。锅锅眼珠骨碌一转，嘴巴开动了。在一个小城镇上，矗立着好几座高楼，住着稀疏的几户人家。楼前的绿化带住着统一的灌木，虽然是绿葱葱的，但并不喜人。在灌木丛里住着花猫一家。花猫妈妈，黑猫爸爸，还有三个才出生不久的小
  • “静悄悄的革命”从教室里萌生出来 右央
    今天通过阅读《静悄悄的革命》译者序和作者序等里面一些句子给我留下了深刻的思考。思考一:作者佐藤学看过数不清的教室和在各个教室里观摩。他发现:“没有哪一个教室和其他教室飘溢着完全相同的气息，或者完全相同的问题。”每个教室都有自己的独特之处，每个教室都带有自己的文化气息。所以，这个教室里的学生必须得到尊重，她们打开自己的心扉，她们的差异得到关注。师生关系是平等的，这样她们才能成为学习的主体。思考二:变
  • Go 面向包的设计和架构分层 云满笔记 golang架构directorylayoutsrcproject
    标题Go面向包的设计和架构分层序前项目架构分层工具包项目应用项目cmd/internal/internal/pkg/pkg/vendor/面向包的设计和验证包的位置依赖包导入应用级别的策略数据的发送和接收错误处理测试捕获错误不建议的目录结论Go面向包的设计和架构分层序本篇内容主要讲解golang项目的面向包设计准则和基础的架构分层。信息来自原文ArdanLabs:Package-Oriented-
  • 明月海潮――美句集锦之四 枫桦陌澜
    序：给予总比承诺多；思念的人丢了魂；打雷是孩子在哭泣；时光的生活演绎了人生……1、承诺是留一点余地，兑现时多一点给予2、细节是成功的砝码3、对面橘黄的灯光穿窗而入，把想家的影子越拽越长4、你不行，是世界上最刻薄的言语；我不行，是对自己最无力的欺骗5、等，翘首以待；发，万念俱灰图片发自App6、夸张的仰望，只因心中幻象迭生7、我不怕打雷，因为我知道他们在哭泣8、我与时光默契的表演，演绎我的人生9、我
  • 《幸福的勇气》摘录其一 小悯丶
    推荐序一、1、在很多人印象里，幸福是一件慵懒的事，就好像学佛是一件随性的事一样。然而恰恰相反，古人说，学佛乃大丈夫事！……真正的修行，首先是放下对恒常的追求，坦然接受无常的发生。这种勇气，没有足够的智慧和福德，是难以拥有的。2、幸福也是一样。如果你所理解的幸福就是什么不开心的事都尽量不发生，平安喜乐地过一辈子，那么多半你是要失望了。3、要选择爱，首先要过伤害这一关。明明遭遇过伤害，却要报之以琼瑶。
  • 寒假开始了 南星南
    明天就开始上寒假班的课程了，一天三个班，6个小时，想想都觉得可怕。从现在开始，要给自己做心理建设了！明天上课我可以！我可以！遇到熊孩子我不气！该做什么做什么，好好备课，讲好课！家长沟通做到位。转年序续班，我最棒！
  • 2022-07-03 回归的只要你愿意
    卷一——个人第一次写作长篇纪实感情文学----别了薇薇安丢失【别了薇薇安】的文稿已经六年,中间的曲折原因不在重述，但是转眼回响，如果，我是说如果当年的几次人生转折点，我是否会仍然像这样的选择呢，或许人生就是如此，你不能掌握什么、决定什么，总有上帝最好、最美善的预备。所以，我还是我---我自孤傲、孑然一身；薇薇安呢，已经有了她最美好的人生，幸福的家庭。我们呢，不复再见。补序于2022年6月24日星期
  • 朱松纯委员：科研条件越来越好，为何颠覆性科学发现却越来越少？ 晨起动铮铎
    原文链接：https://mp.weixin.qq.com/s/2hzjWGcqjzhV0Yob7RmCsg原文转载自科学网文｜《中国科学报》记者赵广立“为什么近年来世界各国科研人员成倍增长、经费越来越多、科研条件越来越好，却产生不了根本性的科学发现？”近日，全国政协委员，北京通用人工智能研究院院长，北京大学、清华大学讲席教授朱松纯在一次发言中发出上述疑问。在他看来，重大基础性原创性科学成果“难产
  • 据谁调查断言余秋雨《文化苦旅》盗版是正版的整整十八倍 徐景洲
    余秋雨先生的《文化苦旅》出版三十年了！当初洛阳纸贵的阅读大潮也波及了我所居住的小城，读书人奔走相告，是文化的狂欢节。但树大招风，争议随之而来。平心而论，我很喜欢《文化苦旅》，但其中坚持不改的硬伤的确难以令人恭维，这可能是余先生离真正的文化大师只差一小步的距离。我也曾在杂志上发过指瑕文，余先生大作找到瑕疵似乎很容易，好像这是他有意设的热炒话题的局。以日前在今日头条上他发表的《文化苦旅》三十年版序为例
  • KMP-看毛片算法 无休居士 数据结构
    #include#includevoidinsert(int*arr,inta,intn){/*0到n-1都已排好序*/inti;intkey=a;for(i=0;i=i;j--){arr[j+1]=arr[j];}arr[i]=key;return;}}arr[n]=key;return;}voidsort(int*arr,intsize){if(size<2)return;inti;for(i
  • 53. 最大子序和 JiangCheng97
    给定一个整数数组nums，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。示例:输入:[-2,1,-3,4,-1,2,1,-5,4],输出:6解释:连续子数组[4,-1,2,1]的和最大，为6。进阶:如果你已经实现复杂度为O(n)的解法，尝试使用更为精妙的分治法求解。方法一：暴力法执行用时:133ms,在MaximumSubarray的Java提交中击败了5.02%的用户内
  • 日记！（2022年7月31日！）。 傅申1980
    日记！！“毅力”！！“坚强”！！“顽强”！！“关键”！！“决定”！！“沉沦”！！（二零二二年，七月三十一日，星期天，凌晨，两点四十五分，左右！！）。（上海市，北部，北部“郊区”，“宝山”区，“写作”者，一“住处”，一普通，“商务”公寓，“写字”楼内，一“破旧”的，小“书房”里！！）。“人”作任何的“事情”，都要“必须”具备“毅力”！！“毅力”是人，“自身力量”的“倍增器”！！有“毅力”的人，往往能
  • 冬季六个节气 mnbvcxz098
    冬季六个《立冬》阴云一夜冷霜凝，万物行藏寻静宁。衰草凄零失袅碧，金菊灿艳竞娉婷。怆然凋柳舞琼絮，萧寂寒江跑素冰。几度轮回休问道，何妨吟啸品清茗。《小雪》地气初沉未酷寒，序届小雪斗西偏。苍天不作阴阳会，旷野难寻骛雁旋。碧水凝眸横玉带，枯枝裹素舞银纨。香腾茗碗催诗兴，佳句捻来韵瑞年。《大雪》时逢大雪酷寒生凛烈朔风侵古城碧水凝眸横玉带青山失黛舞银龙一朝凇塑玲珑景几处冰雕盛世情万籁无声清雅境梅花映日迓春红
  • 冈田武彦与《王阳明大传》 ea41e0427fde
    《王阳明大传》单单是序就有三个版，本书原作者是日本冈田武彦先生，由中国学生钱明译过来。王阳明是中国人，但他的著作却被日本人深为研究，在日本盛行后传回中国，正如序二里说的：阳明学失于吾国而求诸异邦。冈田武彦先生是阳明精神的虔诚践行者，写王阳明大传这套书，历时25年。而看完他对阳明学的贡献，不得不敬佩！1989年3月，由冈田先生发起在日本全国筹集300万日元资助的绍兴县王阳明墓修复工程训练竣工，同年4
  • 蓝桥杯第十四届C++C组 bug～bug～ 蓝桥杯蓝桥杯c++c语言
    目录三国游戏填充翻转【单调队列优化DP】子矩阵【快速幂、欧拉函数】互质数的个数【tire树】异或和之差【质因数分解】公因数匹配子树的大小三国游戏题目描述小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X,Y,Z(一开始可以认为都为0)。游戏有n个可能会发生的事件，每个事件之间相互独立且最多只会发生一次，当第i个事件发生时会分别让X,Y,Z增加Ai,Bi,Ci。当游戏结束时(所有事件的
  • [39]寻找合法字符串-招商银行信用卡中心2018秋 jdzhangxin
    1.题目描述给出一个正整数n，请给出所有的包含n个'('和n个')'的字符串，使得'('和')'可以完全匹配。例如：'(())()'，'()()()'都是合法的；'())()('是不合法的。请按照字典序给出所有合法的字符串。输入描述:输入为1个正整数输出描述:输出为所有合法的字符串，用英文逗号隔开输入示例：2输出示例：(()),()()2.题目解析3.参考答案方法一：构造字符串，并且将字符串排列组
  • 思考：怎样让自己每天都精力充沛 廷伟
    让自己方向坚定，精力充沛的能量法则：Habit习惯能量的倍增Energy精力，能量的来源Attention注意力，能量的转化Target目标，能量的积累这是读张家瑞老师的《能量法则》最重要的四句话。从2018年认识家瑞，一起在AACTP武汉主席峰会一起学习，一起成长，到受他影响，定下更大的目标，践行《职场圆梦手册》，到现在读他的书，更加了解他的经历，一路以来，受他影响颇多。进入地产行业以来，日益忙
  • 小故事|房车之旅之行前准备 杨蔓麦粒鸟
    小故事|房车之旅之行前小准备麦粒鸟亲子邦昨天关注麦粒鸟亲子邦，分享暖心故事陪你观世界才有世界观图片发自原创作者|蔓姐正文字数|1400预计阅读时间|5分钟图片发自网络向往着一场说走就走的旅行有你有我有对生活美好的憧憬序清晨，第一缕阳光洒进房间，缓缓睁开双眼，活络两下再给孩子做早餐，6:30分准时出家门。日复一日，年复一年。曾有人问过我为什么这么早呢？起初可能是因为魔都的早高峰过于可怕，身患密恐的我
  • “延续生命的救命草”-植物非试管高效快繁技术忧遁草 一花一世界灬
    忧遁草（学名：Clinacanthusnutans（Burm.f.）Lindau），别名鳄嘴花、青箭、扭序花。生长环境广泛分布于华南热带至马来西亚、爪哇、加里曼丹。主产于我国热带雨林地区，广东、广西、海南、云南等地都有分布。是一种生长在靠近赤道的低海拔疏林中或灌丛内潮湿砂质土壤里的野生灌木状草本植物，成熟期一般为3--9个月。价值忧遁草是一种营养价值较高的植物，其中的诸多生物活性成分对机体均有一定
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • python 实现euler modified变形欧拉法算法 luthane python算法开发语言
    eulermodified变形欧拉法算法介绍EulerModified（改进）变形欧拉法算法，也被称为欧拉修改法或修正欧拉法（EulerModifiedMethod），是一种用于数值求解微分方程的改进方法。这种方法在传统欧拉法的基础上进行了优化，以减少误差。基本原理欧拉法是一种通过逐步逼近来计算函数值的方法，但在某些情况下，传统的欧拉法可能会引入较大的误差。改进的欧拉法通过使用平均斜率来减小误差。
  • 人体神奇的自愈力，读一遍受益终生 天涯渔夫
    人一生病，就找医生吃药、打针，实际身体越吃越弱，下一次用药的剂量可能就要成倍增加，特别是抗生素效果还会递减……其实，人体有你想象不到的强大自愈力。图片发自App“自愈力是人体与生俱来的潜能，具有巨大的神奇力量，不会因年龄增大而消失”。1、60％的疾病都能自愈德国《生机》杂志2006年刊登的一篇文章：研究人员发现，只要注意调养和改善生活习惯，60％—70％的疾病都能够自愈。这与洪昭光教授曾在接受《生
  • 五维教练领导力为团队赋能 赵国涛_d512
    学习完陈序老师的五维教练领导力，通过复盘领悟教练领导力的一些核心思想，把它用到公司团队的培训中。通过对员工不断的激发，教练式的引导，让团队每个人看到了更多的可能性，完成了我们公司好多难以完成的业绩目标。针对公司的管理团队，让大家在培训中学会欣赏对方，学会倾听，学会用正能量去感染团队的每个人，增强了公司管理团队的凝聚力，让大家成为每位下属的教练，角色的转变，让管理人员更有责任感，更相信团队的力量。五
  • c语言输入两个字符串 按字典数序比较大小,算法学习笔记（一）C++排序函数、映射技巧与字典树... Nature自然科研 c语言输入两个字符串按字典数序比较大小
    1.头文件algorithm中有函数sort()用于排序，参数为：排序起始地址，排序结束地址，排序规则(返回bool型)例如，要将array[]={5,7,1,2,9}升序排列，则使用：boolcmp(inta,intb);intmain(){intarray[]={5,7,1,2,9};sort(array,array+5,cmp);for(inti=0;icoutb)returnfalse;e
  • 刚体运动描述：欧拉角与四元数 FL17171314 算法
    姿态角偏差主要有三种描述方式：欧拉角误差，轴角误差和四元数误差。在机器人学中，刚体的运动描述是非常重要的，特别是当我们需要精确控制机器人的姿态时。欧拉角和四元数是两种常用的描述刚体在三维空间中旋转的方法。下面将分别介绍这两种方法并给出其特点。欧拉角定义与特点：定义：欧拉角是通过绕一个三维坐标系的三个轴依次旋转来定义的，通常按照某个固定的旋转顺序（如XYZ、ZYX等）进行。表示：欧拉角由三个角度组成
  • 暑期破防实录——捡漏腾讯 沈七QWQ 沈七杂谈前端程序人生面试
    序经历了整整三个月的折磨，暑期实习终于尘埃落定。其实还没收到offer的时候，还会想着到时候录用了该怎么大写特写小作文，但真到了这一天，只剩下一种解脱感，一种摆脱了漫长的焦虑与压抑的淡淡喜悦。或许就像久病之人终于重获健康那样，虽然治愈了，但已然疲惫不堪。现在，我只渴望休息，去睡一个漫长而安稳的觉，能安心的赖床而不自责。不用再机械地刷新牛客动态，而不知道自己到底想要什么。原来就只是这种感觉，周围的一
  • 杜娟11月2日读《赠郭善甫归省序》有感： 杜娟A
    杜娟11月2日读《赠郭善甫归省序》有感：先生曰：“夫志犹种也，学问思辩而笃行之，是耕耨灌溉以求于有秋也”。其实他把立志比喻成农民种庄稼一样，需要种子，种子耕进土地里以后，需要深耕细作，及时除草，及时施肥，及时灌溉，才能有好的收获。志向也就向种子一样，需要通过博学、审问、慎思，明辩，笃行，如果我们把这些做扎实了，功到自然而成。也正如阳明先生所立下的志向：“唯读书学圣贤耳”。总之通过反复阅读原文，深入
  • Maven Array_06 eclipsejdkmaven
    Maven Maven是基于项目对象模型(POM)， 信息来管理项目的构建，报告和文档的软件项目管理工具。 Maven 除了以程序构建能力为特色之外，还提供高级项目管理工具。由于 Maven 的缺省构建规则有较高的可重用性，所以常常用两三行 Maven 构建脚本就可以构建简单的项目。由于 Maven 的面向项目的方法，许多 Apache Jakarta 项目发文时使用 Maven，而且公司
  • ibatis的queyrForList和queryForMap区别 bijian1013 javaibatis
    一.说明         iBatis的返回值参数类型也有种：resultMap与resultClass，这两种类型的选择可以用两句话说明之：         1.当结果集列名和类的属性名完全相对应的时候，则可直接用resultClass直接指定查询结果类
  • LeetCode[位运算] - #191 计算汉明权重 Cwind java位运算LeetCodeAlgorithm题解
    原题链接：#191 Number of 1 Bits 要求： 写一个函数，以一个无符号整数为参数，返回其汉明权重。例如，‘11’的二进制表示为'00000000000000000000000000001011', 故函数应当返回3。 汉明权重：指一个字符串中非零字符的个数；对于二进制串，即其中‘1’的个数。 难度：简单 分析： 将十进制参数转换为二进制，然后计算其中1的个数即可。 “
  • 浅谈java类与对象 15700786134 java
          java是一门面向对象的编程语言，类与对象是其最基本的概念。所谓对象，就是一个个具体的物体，一个人，一台电脑，都是对象。而类，就是对象的一种抽象，是多个对象具有的共性的一种集合，其中包含了属性与方法，就是属于该类的对象所具有的共性。当一个类创建了对象，这个对象就拥有了该类全部的属性，方法。相比于结构化的编程思路，面向对象更适用于人的思维
  • linux下双网卡同一个IP 被触发 linux
    转自： http://q2482696735.blog.163.com/blog/static/250606077201569029441/ 由于需要一台机器有两个网卡，开始时设置在同一个网段的IP，发现数据总是从一个网卡发出，而另一个网卡上没有数据流动。网上找了下，发现相同的问题不少： 一、 关于双网卡设置同一网段IP然后连接交换机的时候出现的奇怪现象。当时没有怎么思考、以为是生成树
  • 安卓按主页键隐藏程序之后无法再次打开 肆无忌惮_ 安卓
    遇到一个奇怪的问题，当SplashActivity跳转到MainActivity之后，按主页键，再去打开程序，程序没法再打开（闪一下），结束任务再开也是这样，只能卸载了再重装。而且每次在Log里都打印了这句话"进入主程序"。后来发现是必须跳转之后再finish掉SplashActivity   本来代码：   // 销毁这个Activity fin
  • 通过cookie保存并读取用户登录信息实例 知了ing JavaScripthtml
    通过cookie的getCookies()方法可获取所有cookie对象的集合；通过getName()方法可以获取指定的名称的cookie；通过getValue()方法获取到cookie对象的值。另外，将一个cookie对象发送到客户端，使用response对象的addCookie()方法。 下面通过cookie保存并读取用户登录信息的例子加深一下理解。 （1）创建index.jsp文件。在改
  • JAVA 对象池 矮蛋蛋 javaObjectPool
    原文地址： http://www.blogjava.net/baoyaer/articles/218460.html Jakarta对象池       ☆为什么使用对象池   恰当地使用对象池化技术，可以有效地减少对象生成和初始化时的消耗，提高系统的运行效率。Jakarta Commons Pool组件提供了一整套用于实现对象池化
  • ArrayList根据条件+for循环批量删除的方法 alleni123 java
    场景如下： ArrayList<Obj> list Obj-> createTime, sid. 现在要根据obj的createTime来进行定期清理。（释放内存） ------------------------- 首先想到的方法就是 for(Obj o:list){ if(o.createTime-currentT>xxx){
  • 阿里巴巴“耕地宝”大战各种宝 百合不是茶 平台战略
    “耕地保”平台是阿里巴巴和安徽农民共同推出的一个 “首个互联网定制私人农场”，“耕地宝”由阿里巴巴投入一亿 ，主要是用来进行农业方面，将农民手中的散地集中起来 不仅加大农民集体在土地上面的话语权，还增加了土地的流通与 利用率，提高了土地的产量，有利于大规模的产业化的高科技农业的 发展，阿里在农业上的探索将会引起新一轮的产业调整，但是集体化之后农民的个体的话语权 将更少，国家应出台相应的法律法规保护
  • Spring注入有继承关系的类（1） bijian1013 javaspring
    一个类一个类的注入 1.AClass类 package com.bijian.spring.test2; public class AClass { String a; String b; public String getA() { return a; } public void setA(Strin
  • 30岁转型期你能否成为成功人士 bijian1013 成功
            很多人由于年轻时走了弯路，到了30岁一事无成，这样的例子大有人在。但同样也有一些人，整个职业生涯都发展得很优秀，到了30岁已经成为职场的精英阶层。由于做猎头的原因，我们接触很多30岁左右的经理人，发现他们在职业发展道路上往往有很多致命的问题。在30岁之前，他们的职业生涯表现很优秀，但从30岁到40岁这一段，很多人
  • [Velocity三]基于Servlet+Velocity的web应用 bit1129 velocity
    什么是VelocityViewServlet 使用org.apache.velocity.tools.view.VelocityViewServlet可以将Velocity集成到基于Servlet的web应用中，以Servlet+Velocity的方式实现web应用   Servlet + Velocity的一般步骤 1.自定义Servlet，实现VelocityViewServl
  • 【Kafka十二】关于Kafka是一个Commit Log Service bit1129 service
    Kafka is a distributed, partitioned, replicated commit log service.这里的commit log如何理解？   A message is considered "committed" when all in sync replicas for that partition have applied i
  • NGINX + LUA实现复杂的控制 ronin47 lua nginx 控制
    安装lua_nginx_module 模块 lua_nginx_module 可以一步步的安装，也可以直接用淘宝的OpenResty Centos和debian的安装就简单了。。 这里说下freebsd的安装： fetch http://www.lua.org/ftp/lua-5.1.4.tar.gz tar zxvf lua-5.1.4.tar.gz cd lua-5.1.4 ma
  • java-14.输入一个已经按升序排序过的数组和一个数字， 在数组中查找两个数，使得它们的和正好是输入的那个数字 bylijinnan java
    public class TwoElementEqualSum { /** * 第 14 题： 题目：输入一个已经按升序排序过的数组和一个数字， 在数组中查找两个数，使得它们的和正好是输入的那个数字。 要求时间复杂度是 O(n) 。如果有多对数字的和等于输入的数字，输出任意一对即可。 例如输入数组 1 、 2 、 4 、 7 、 11 、 15 和数字 15 。由于
  • Netty源码学习-HttpChunkAggregator-HttpRequestEncoder-HttpResponseDecoder bylijinnan javanetty
    今天看Netty如何实现一个Http Server org.jboss.netty.example.http.file.HttpStaticFileServerPipelineFactory： pipeline.addLast("decoder", new HttpRequestDecoder()); pipeline.addLast(&quo
  • java敏感词过虑-基于多叉树原理 cngolon 违禁词过虑替换违禁词敏感词过虑多叉树
    基于多叉树的敏感词、关键词过滤的工具包，用于java中的敏感词过滤 1、工具包自带敏感词词库，第一次调用时读入词库，故第一次调用时间可能较长，在类加载后普通pc机上html过滤5000字在80毫秒左右，纯文本35毫秒左右。   2、如需自定义词库，将jar包考入WEB-INF工程的lib目录，在WEB-INF/classes目录下建一个 utf-8的words.dict文本文件，
  • 多线程知识 cuishikuan 多线程
    T1，T2，T3三个线程工作顺序，按照T1，T2，T3依次进行 public class T1 implements Runnable{           @Override      
  • spring整合activemq dalan_123 java spring jms
    整合spring和activemq需要搞清楚如下的东东1、ConnectionFactory分：     a、spring管理连接到activemq服务器的管理ConnectionFactory也即是所谓产生到jms服务器的链接      b、真正产生到JMS服务器链接的ConnectionFactory还得
  • MySQL时间字段究竟使用INT还是DateTime？ dcj3sjt126com mysql
      环境：Windows XPPHP Version 5.2.9MySQL Server 5.1 第一步、创建一个表date_test（非定长、int时间） CREATE TABLE `test`.`date_test` (`id` INT NOT NULL AUTO_INCREMENT ,`start_time` INT NOT NULL ,`some_content`
  • Parcel: unable to marshal value dcj3sjt126com marshal
    在两个activity直接传递List<xxInfo>时，出现Parcel: unable to marshal value异常。   在MainActivity页面（MainActivity页面向NextActivity页面传递一个List<xxInfo>）：   Intent intent = new Intent(this, Next
  • linux进程的查看上（ps） eksliang linux pslinux ps -llinux ps aux
    ps:将某个时间点的进程运行情况选取下来 转载请出自出处：http://eksliang.iteye.com/admin/blogs/2119469 http://eksliang.iteye.com         ps 这个命令的man page 不是很好查阅，因为很多不同的Unix都使用这儿ps来查阅进程的状态，为了要符合不同版本的需求，所以这个
  • 为什么第三方应用能早于System的app启动 gqdy365 System
    Android应用的启动顺序网上有一大堆资料可以查阅了，这里就不细述了，这里不阐述ROM启动还有bootloader，软件启动的大致流程应该是启动kernel -> 运行servicemanager 把一些native的服务用命令启动起来（包括wifi, power, rild, surfaceflinger, mediaserver等等）-> 启动Dalivk中的第一个进程Zygot
  • App Framework发送JSONP请求(3) hw1287789687 jsonp跨域请求发送jsonpajax请求越狱请求
    App Framework 中如何发送JSONP请求呢? 使用jsonp,详情请参考:http://json-p.org/ 如何发送Ajax请求呢? (1)登录 /*** * 会员登录 * @param username * @param password */ var user_login=function(username,password){ // aler
  • 发福利，整理了一份关于“资源汇总”的汇总 justjavac 资源
    觉得有用的话，可以去github关注：https://github.com/justjavac/awesome-awesomeness-zh_CN 通用 free-programming-books-zh_CN 免费的计算机编程类中文书籍 精彩博客集合 hacke2/hacke2.github.io#2 ResumeSample 程序员简历
  • 用 Java 技术创建 RESTful Web 服务 macroli java编程WebREST
    转载：http://www.ibm.com/developerworks/cn/web/wa-jaxrs/   JAX-RS (JSR-311) 【 Java API for RESTful Web Services 】是一种 Java™ API，可使 Java Restful 服务的开发变得迅速而轻松。这个 API 提供了一种基于注释的模型来描述分布式资源。注释被用来提供资源的位
  • CentOS6.5-x86_64位下oracle11g的安装详细步骤及注意事项 超声波 oraclelinux
    前言： 这两天项目要上线了，由我负责往服务器部署整个项目，因此首先要往服务器安装oracle，服务器本身是CentOS6.5的64位系统，安装的数据库版本是11g，在整个的安装过程中碰到很多的坑，不过最后还是通过各种途径解决并成功装上了。转别写篇博客来记录完整的安装过程以及在整个过程中的注意事项。希望对以后那些刚刚接触的菜鸟们能起到一定的帮助作用。   安装过程中可能遇到的问题（注
  • HttpClient 4.3 设置keeplive 和 timeout 的方法 supben httpclient
    ConnectionKeepAliveStrategy kaStrategy = new DefaultConnectionKeepAliveStrategy() { @Override public long getKeepAliveDuration(HttpResponse response, HttpContext context) { long keepAlive
  • Spring 4.2新特性-@Import注解的升级 wiselyman spring 4
    3.1 @Import @Import注解在4.2之前只支持导入配置类 在4.2,@Import注解支持导入普通的java类,并将其声明成一个bean 3.2 示例 演示java类 package com.wisely.spring4_2.imp; public class DemoService { public void doSomethin
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他