树状数组学习笔记
本文是笔者学完树状数组后对树状数组进行的一个学习总结,如有纰漏或者错误之处,还望读者不吝指教,不胜感激!
一、树状数组的概念:
所谓树状数组(Binary Indexed Tree),从字面意思来讲,就是用数组来模拟树形结构。也就是说它可以将线性结构转化为树形结构,从而实现跳跃式的扫描。所以它一般应用于解决动态前缀和问题。
二、树状数组一般可以解决的问题:
树状数组可以解决大部分基于区间上的更新和求和问题。但功能有限,遇到一般的复杂问题是不能解决的。
三、和线段树的区别:
所有可以用树状数组解决的问题都可以用线段树解决。但树状数组的代码复杂度明显优于线段树。所以可以使用树状数组解决的问题都可以尽量考虑用树状数组解决。(当然,神牛请随意)
四、时间复杂度和空间复杂度:
树状数组修改和查询的时间复杂度都是O(logN),空间复杂度为O(N)
下面我将从树状数组的创建到树状数组可以实现的各个功能开始逐一讲解。
1、树状数组的创建:
讲解二叉树的结构之前,我先引入二叉树的结构,如图下图所示:
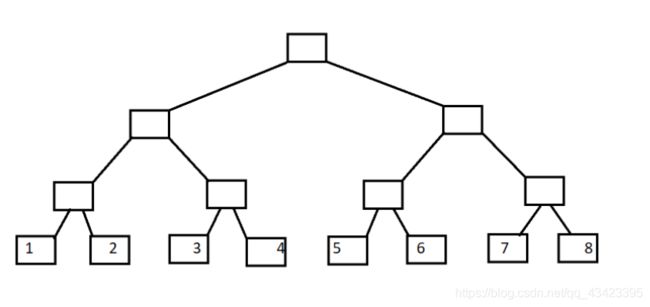
这样每一个父亲节点都存的是两个子节点的值,那就可以解决一般的基于区间的查询和修改问题,但这样的树形结构是线段树,不是树状数组。所以树状数组是一个什么样的树形结构呢?
首先,我们把二叉树的结构变形一下:
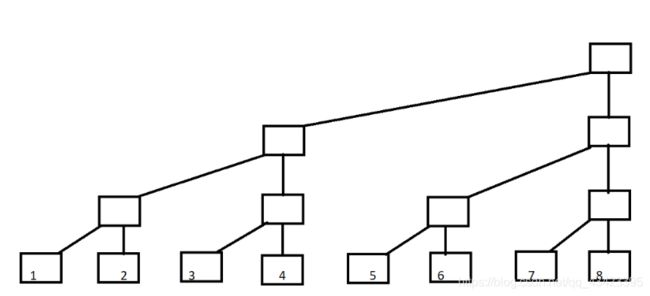
之后,在删掉部分结点,如下图所示:
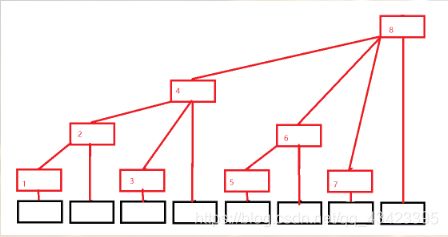
黑色数组表示原来的数组A[i],红色代表树状数组C[i],看上图,则有:
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
从这我们就可以看出一些规律来:
C[i]=A[i- 2 k 2^{k} 2k+1]+A[i- 2 k 2^{k} 2k+2]+…A[i]; (k为i的二进制中末尾0的数量)
例如i=8时,k=3;
这样,树状数组就算建立成功啦!
那我们如何才能将 2 k 2^{k} 2k取出来呢?
这里引入lowbit(x)函数如下:
int lowbit(int x) {
return x & (-x);
}
这个函数就可以将x的最后一位“1”即 2 k 2^{k} 2k取出来。为什么呢?
比如x = 12,将其转化为二进制表示为01100(第一位是符号位)
则-12的二进制表示为10100(第一位也是符号位)
则x&(-x) = 00100。
由此可见,lowbit(x)函数确实可以将x的最后一位“1”取出来!
2、单点修改,区间查询:
由上图的树状数组结构图我们知道,C[]数组是跳跃性的存储某些结点的和。比如我在A[1]的位置加上1,那么C[1],C[2],C[4] …都要+1,所以用代码实现如下:
void update(int x,LL y) {
for(int i = x ; i <= n ; i += lowbit(i)) {
C[i] += y;
}
}
至于区间求和,而且参考上述的树状数组结构图,
比如 ∑ i = 1 7 \sum_{i=1}^{7} ∑i=17 = C[7] + C[6] + C[4];就是相当于每次加上二进制减去最后一的位置的值。代码实现如下:
LL query(int x) {
LL ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) {
ans += C[i];
}
return ans;
}
3、区间修改,单点求和:
树状数组可以直接解决单点修改以及区间求和问题,但如何实现区间修改和区间求和呢?首先我们引入差分数组:
a[1] = A[1] - A[0];
a[2] = A[2] - A[1];
a[3] = A[3] - A[2];
…
a[n] = A[n] - A[n-1];
(A[]数组下标从1开始,A[0] = 0)
这样我们用树状数组维护A[i] - A[i-1]就好,这样a[i]得前n项和就是
A[n] - A[0] = A[n]。
区间修改呢?比如我要[1,3] + 3,
那我需要做的就是a[1] += 3 ,a[4] -= 3,为什么呢?
更新之后:
a[1] = A[1] - A[0] + 3;
a[2] = A[2] - A[1];
a[3] = A[3] - A[2];
a[4] = A[4] - A[3] - 3.
这样,根据前面得区间求和得叙述,我们知道,差分数组前n项和就是第n项得值,此时
a[1] = A[1] + 3;
a[1] + a[2] = A[2] + 3;
a[1] + a[2] + a[3] = A[3] + 3;
a[1] + a[2] + a[3] + a[4] = A[4].
这样不就实现了[1,3] + 3的功能了嘛!!!
是不是很神奇?
具体代码可以参考树状数组区间修改,单点求和例题
AC代码如下:
#include 4、区间修改,区间求和:
与上一个区间修改,单点查询类型,区间修改,区间查询还是基于差分。
首先考虑a[i] = A[i] - A[i-1];
那么A[i] = ∑ j = 1 i \sum_{j=1}^{i} ∑j=1ia[j],则
∑ i = 1 n \sum_{i=1}^{n} ∑i=1nA[i] = ∑ i = 1 n \sum_{i=1}^{n} ∑i=1n ∑ j = 1 i a [ j ] \sum_{j=1}^{i}a[j] ∑j=1ia[j] = a[1] + a[1] + a[2] + a[1] + a[2] + a[3] + …
=n*a[1] + (n-1)*a[2] + (n-2)*a[3] + …
= ∑ i = 1 n \sum_{i=1}^{n} ∑i=1n(n-i+1)a[i] = (n+1)* ∑ i = 1 n \sum_{i=1}^{n} ∑i=1na[i] - ∑ i = 1 n \sum_{i=1}^{n} ∑i=1ni*a[i];
所以呢,我们只需要维护两个树状数组a[i] 和i*a[i]就可以实现树状数组区间修改,区间求和功能。
具体代码可看这道例题。
AC代码如下:
#include 5、二维树状数组:
以上我讲解的所有的内容都属于一维树状数组,至于二维树状数组,它维护的是一个矩阵。他的更新和修改操作可以直接又一维树状数组直接递推过去。
(1)、单点更新,区间求和:
二维树状数组单点修改代码如下:
void update(int x,int y,int val) {
for(int i = x ; i <= n ; i += lowbit(i)) {
for(int j = y ; j <= m ; j += lowbit(j)) {
c[i][j] += val;
}
}
}
区间查询代码如下:
LL query(int x,int y) {
LL ans = 0;
for(int i = x ; i > 0 ; i -= lowbit(i)) {
for(int j = y ; j > 0 ; j -= lowbit(j)) {
ans += c[i][j];
}
}
return ans;
}
下面,我们可以看一道二维树状数组的例题(hdu1892)
这就是二维树状数组的模板题,包括二维树状数组单点更新和区间求和。
其中题目要求一共有四种操作:
S x1 y1 x2 y2 :求区间(x1,y1) -> (x2,y2)的和;
A x1 y1 n1:(x1,y1) + n1;
D x1 y1 n1 :(x1,y1) - n1,注意(x1,y1)的值不会小于0;
M x1 y1 x2 y2 n1:(x1,y1) - n1 , (x2,y2) + n1。注意(x1,y1)不会小于0;
代码如下:
#include
#include (2)、区间更新,单点求和:
这里,我们还是要建立差分数组a[i][j] = A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1]
这样query(x,y)求出的就是A[i][j]啦。
那区间更新如何实现呢?
比如下面有一个初始的差分二维矩阵:
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
现在我要将(2,2)到(4,4)的全部加上x如何做呢?
如下图所示:
0 0 0 0 0
0 +x 0 0 -x
0 0 0 0 0
0 0 0 0 0
0 -x 0 0 +x
这样,求和以后的矩阵如下所示:
0 0 0 0 0
0 x x x 0
0 x x x 0
0 x x x 0
0 0 0 0 0
这样,二维树状数组的区间更新,单点求和就算完成啦。
具体代码可看一道例题:poj2155
这道题给你一个初始全为0的矩阵,之后有两种操作:
C x1,y1,x2,y2:给(x1,y1)到(x2,y2)区间里的数全部取反
Q x,y:查询坐标(x,y)的值。
这就是一个典型的二维数组区间更新,单点求和的题,代码如下:
#include
#include (3)、区间修改,区间求和:
我们考虑区间求和,点(x,y)的二维前缀和为
∑ i = 1 x ∑ j = 1 y ∑ h = 1 i ∑ k = 1 j a [ h ] [ k ] \sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{h=1}^{i}\sum_{k=1}^{j}a[h][k] i=1∑xj=1∑yh=1∑ik=1∑ja[h][k]
其中a[i][j] = A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1]
这样,我们统计一下,就可以得到a[i][j]在上述等式中一共出现了(x-i+1)*(y-j+1)次,这样,我们可以将式子化简一下,得
∑ i = 1 x ∑ j = 1 y ( x − i + 1 ) ∗ ( y − j + 1 ) ∗ a [ i ] [ j ] \sum_{i=1}^{x}\sum_{j=1}^{y}(x-i+1)*(y-j+1)*a[i][j] i=1∑xj=1∑y(x−i+1)∗(y−j+1)∗a[i][j]
化简一下,得
( x + 1 ) ∗ ( y + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y a [ i ] [ j ] (x+1)*(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}a[i][j] (x+1)∗(y+1)∗i=1∑xj=1∑ya[i][j]
− ( y + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y i ∗ a [ i ] [ j ] - (y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}i*a[i][j] −(y+1)∗i=1∑xj=1∑yi∗a[i][j]
− ( x + 1 ) ∗ ∑ i = 1 x ∑ j = 1 y j ∗ a [ i ] [ j ] - (x+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}j*a[i][j] −(x+1)∗i=1∑xj=1∑yj∗a[i][j]
+ ∑ i = 1 x ∑ j = 1 y i ∗ j ∗ a [ i ] [ j ] + \sum_{i=1}^{x}\sum_{j=1}^{y}i*j*a[i][j] +i=1∑xj=1∑yi∗j∗a[i][j]
所以我们更具等式维护四个树状数组就好
具体代码我们可以更具一道例题来讲
题意就是二维数组区间修改,区间求和,具体代码如下:
#include
#include 6、树状数组离线操作。
这个我就根据具体的例题来说明啦。
例一:洛谷P1972
题意:给你n个数,m次操作,每次操作问区间[L,R]的范围内有多少个不同的数。
思路分析:这一题用数组数组来做,各位可以去看这位大佬题解,他写的非常明白(我在写的话也不过是把他的话重复一遍)。
AC代码:
#include
#include 例二:hdu3333
题意:给你n个数,m次操作,每次操作问你区间[l,r]内不同的数的和。
思路分析:这一题和上一题几乎一模一样,不过由于a[]特别大,所以要离散化,具体详见代码。
AC代码:
#include
#include