【回溯】B028_LQ_完美正方形（换行深搜+剪枝）

如果一些边长互不相同的正方形，可以恰好拼出一个更大的正方形，则称其为完美正方形。

历史上，人们花了很久才找到了若干完美正方形。

比如：如下边长的 22 个正方形：2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60

如图这样组合，就是一种解法

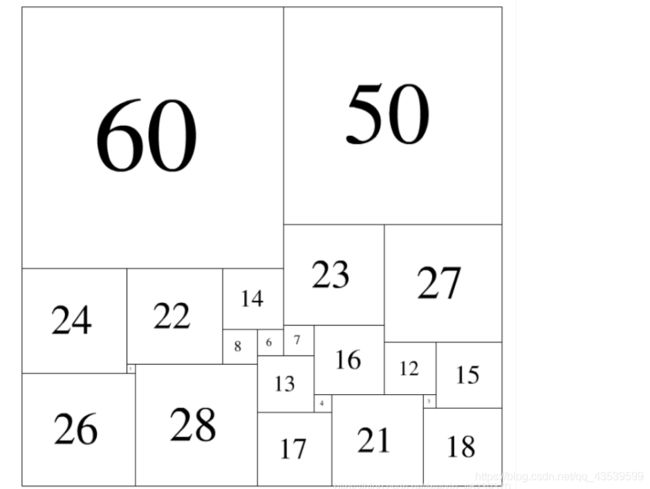
此时，紧贴上边沿的是：60 50，紧贴下边沿的是：26 28 17 21 18

22 阶完美正方形一共有 8 种

右边的组合是另一种：2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61

如果告诉你该方案紧贴着上边沿的是从左到右依次为：47 46 61，你能计算出紧贴着下边沿的是哪几个正方形吗？

方法一：深搜+剪枝

思路

长 n = 47+46+61 = 154， 宽 m = n =154；在填数的时候应确保位置 (i, j)：

• 该位置上没有填数；
• 在该位置填上数后，不越界

剪枝：dfs 循环中，如果小的正方形放不下时，应该立即 break

#include
using namespace std;

const int N=155, EMPTY=0, A[22]={2,5,9,11,16,17,19,21,22,24,26,30,31,33,35,36,41,50,52};
int g[N+5][N+5], printed[N+5], vis[22];

void put(int x, int y, int sz, int v) {
    for (int i=x; i<x+sz; i++)
    for (int j=y; j<y+sz; j++) {
        g[i][j]=v;
    }
}
void print_ans() {
    for (int j=1; j<=N; j++) if (!printed[g[N][j]]) {
        printf("%d ", g[N][j]);
        printed[g[N][j]]=true;
    }
}

bool chk(int x, int y, int sz) {
    if (x+sz>N || y+sz>N) return false;
    for (int i=x; i<x+zs; i++)
    for (int j=y; j<y+sz; j++) {
        if (g[i][j] != EMPTY) return false;
    }
    return true;
}
void dfs(int x, int y) {
    if (y==N-1) x++, y=1;
    if (x==N) {
        print_ans();
        return;
    }
    if (g[x][y]==EMPTY) {
        for (int k=0; k<22; k++) if (!vis[k] && chk(x, y, A[k])) {
            vis[k]=1;
            put(x, y, A[k], A[k]);
            dfs(x, y+A[k]);
            vis[k]=0;
            put(x, y, A[k], 0);
        }
    } else {
        dfs(x, y+1);
    }
}
int main() {
    put(1, 1, 47, 47);
    put(1, 48, 46, 46);
    put(1, 94, 61, 61);
    dfs(47, 1);
    return 0;
}