1.prim算法分析
prim算法是用来构建MST(最小生成树)的一种基于贪心策略的算法。prim算法通过维护lowcost数组和closest数组记录每次查询的最小权值边结点。
首先,看一个示例来理解prim算法是怎样构建最小生成树的。我们现在对图a从结点V1开始构建最小生成树,在右边的是当前图的邻接矩阵。
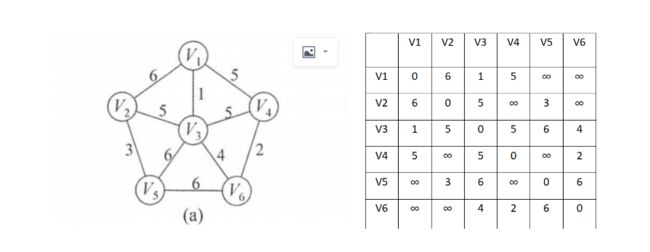
1.先初始化一个lowcost数组和closest数组,并且让lowcost的初始值为v1行的值。让closest数组的值为v1。

2.找到lowcost数组中的最小值(权值为0表示没有边,故非0的最小值),然后记录最小权值和位置,并且加入到最小生成树中。
此时Min = 3,mindex = 3;表示(V1,V3)是本次找到的最小值边,加入MST中,并切将lowcost[mindex]的置为0,表示结点已经加入MST。
3.依据加入的结点V3,更新lowcost数组和closest数组的值。其中Closest中值代表本次查找过程中,权值为lowcost[j]的边是连接MST中哪个结点的。

4.以此循环2~3步骤,直到所有结点加入到MST中。
#include
#include
#include
using namespace std;
#defind MAX 6;
#define MAXCOST 0x7fffffff
typedef String VertexType;
typedef int EdgeType;
typedef struct {
VertexType Vex[MAX];
EdgeType Edge[MAX][MAX];
int vexnum,arcnum;
}MGragh;
void prim(MGraph G, VertexType v){
int lowcost[MAX]; //lowcost数组用来更新不在MST中的结点到MST的权值最小的节点;
int closest[MAX]; //closest数组用来储存是通过哪个结点找到的最小权值边;通过找到MST的边;
int i, j,mindex,min; //mindex用来记录每次查找的最小权值边的结点; min记录每次查找到的最小权值;
//初始化 让lowcost[]的值为与v相邻的边的权值。让closest[]的值为v;
for(int i=0;i 2.Kruskal算法分析
kruskal算法也是构建生成树的一种贪心算法,它与prim算法的区别在于:kruskal主要将图中边作为处理对象。它先将图中所有的边信息储存到一个边集合中,然后选择集合中最小权值的边,并且利用vset记录相当边的2个结点是否属同一个集合,若是,则不加入MST中,若不是,则加入MST中。
我们现在对图a利用kurskal算法开始构建最小生成树,在右边的是当前图的邻接矩阵
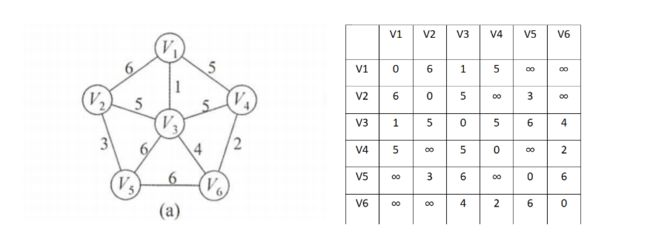
1.初始化一个边集E,和一个辅助数组vset[]用来判断一条边的2个顶点是否属于同一个集合。
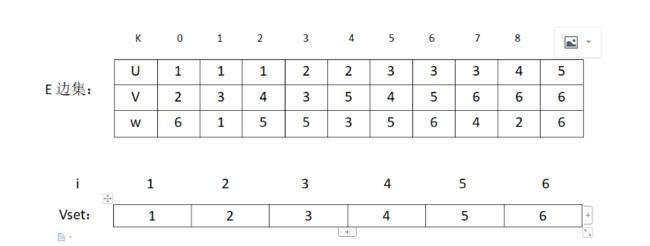
2.然后通过排序算法对边集E排序,选择出最小的权值边。判断选出的边(u,v)是否属于同一集合,判断方法是比较vset[u]和vset[v]的值是否一样。若是一样,则属于同一个集合,不加入MST。若不是则修改所有vset[i] = v的结点让它的值为u ,表示结点u和v所在的集合加入同一集合了。
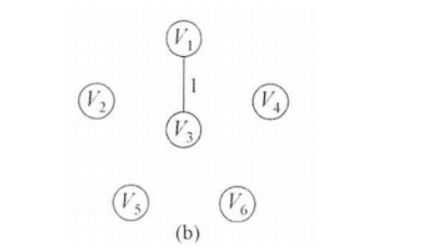
如:通过堆排序找到了最小权值边(1,3)然后判断vset[1]和vset[3]值是否相同,发现不相同,则加入MST,然后修改vset[3] =vset[1]。执行后表的状态为:
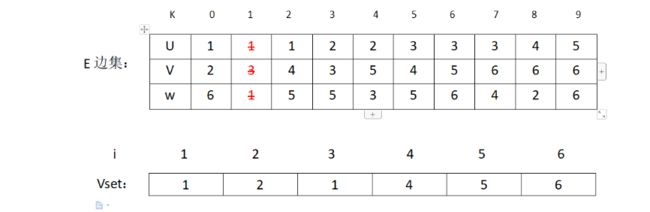
对应的图的状态为:
接下来是边(4,6),它的权值为2。判断发现结点v4,v6不是同一集合,加入MST。修改表格

对应图的状态为:

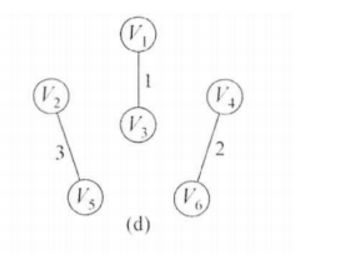
接下来是(2,5)权值为3,然后加入MST,修改表格

对应图的状态:
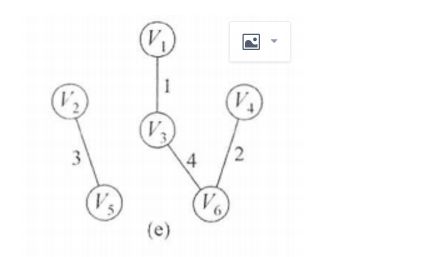
接下来是边(3,6),V3和V6也不是同一集合,加入MST。修改表格:

对应图的状态:
接下来是边(1,4)v1和v4属于同一集合,则不加入MST。表格为:

接下来是(2,3) v2和v3不在同一个集合,加入MST,修改表格:
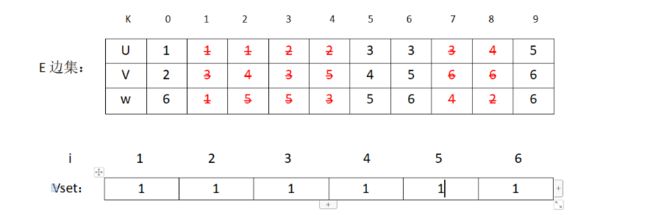
对应图状态为:

到此,所有的结点都在同一集合,MST构建完毕。
typedef struct{
char vertex[VertexNum]; //顶点表
int edges[VertexNum][VertexNum]; //邻接矩阵,可看做边表
int n,e; //图中当前的顶点数和边数
}MGraph;
typedef struct node {
int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
}Edge;
void kruskal(MGraph G){
int i,j,u1,v1,sn1,sn2,k;
int vset[VertexNum]; //辅助数组。判定两个顶点是否连通
Edge E[EdgeNum]; //存放全部的边
k=0; //E数组的下标从0開始
//
for (i=0;i %d, %d",E[j].u,E[j].v,E[j].w);
k++;
for (i=0;i 