优先队列式_分支限界法_TSP旅行商问题问题
最近真的好久没有更了,会陆续更一些算法问题,有需要的朋友请查看哦!欢迎大家与我交流~
一起学习一起进步哦~
问题:
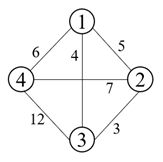
某售货员要去n个城市推销商品,该售货员从一个城市出发,经过每个城市一次,最后回到起始城市。应如何选择行进路线,以使总的路程最短。设n=4, 城市与城市之间的费用如图所示。采用优先队列式分支限界算法解决该问题。
 import java.util.Scanner;
import java.util.Scanner;
public class BBTSP {
//排列树结点描述类
private static class HeapNode implements Comparable
{ int s; //s 表示结点在排列树中的层次,根结点到当前结点的路径为x[0:s]
float lcost; //子树费用的下界
float cc; //当前费用
float rcost; //x[s:n-1]中顶点最小出边费用和
int [ ] x; //需要进一步搜索的顶点是x[s+1, n-1]
//构造方法
HeapNode(float lc,float ccc,float rc,int ss,int [ ]xx)
{ lcost=lc;
cc=ccc;
rcost=rc;
s=ss;
x=xx;
}
@Override
public int compareTo(Object o) {
return 0;
}
}
//图G的邻接矩阵
static float [ ][ ]a;
static int n;
//最小堆描述
public static class MinHeap{
static HeapNode[] h;//活结点表
private static int front;//堆顶引用,若堆不空,指向堆顶元素
private static int rear;//堆尾引用,若堆不空,指向堆尾元素的下一个位置
public MinHeap(HeapNode[] h,int a,int b) {
front=rear=0;
this.h=h;
}
//筛选法调整堆
//将以low为根结点的子树调整成小顶堆,low和high分别是待调整序列的上界和下界
static void sift(int low,int high) {
int i=low;//子树的根结点
int j=2*i+1;//j为i结点的左孩子
HeapNode temp=h[i];
while(jh[j+1].lcost) {
j++;//结点优先级进行比较,j为左右孩子结点的较小者
}
if(temp.lcost>h[j].lcost) {//若父母结点值较大
h[i]=h[j];//孩子结点的较小者上移
i=j;
j=2*j+1;//对以被交换的子结点作为根结点所在的子树进行调整
}else {
j=high+1;//退出循环
}
}
h[i]=temp;//当前子树的原根值调整后的位置
}
//创建堆算法
static void insertheapSort() {
int n=rear-front;//待加入堆的结点个数
HeapNode temp;
for(int i=n/2-1;i>=front;i--) {//创建堆
sift(i,n);
}
}
//取出堆顶元素,并且重新调整堆为最大堆的算法
static HeapNode removeheapSort() {
int n=rear-front;//
int i=n-1;//堆的最后一个结点
HeapNode temp=h[front];
h[front]=h[i];//将堆中最大关键字值移到最前面
sift(front,i);//并且调整成堆
return temp;//返回最顶堆结点
}
//将堆元素node加入堆,并且调整堆
public void insert(HeapNode node) {
h[rear]=node;
rear+=1;//修改尾指针
insertheapSort();//调整堆
}
public HeapNode removemin() {
HeapNode temp=removeheapSort();
rear-=1;
return temp;
}
}
//求出这棵树的minsum
public static float bbTSP(int[] v)
{ //解货郎担问题的优先队列式分支限界法
HeapNode []h1=new HeapNode[n+1];
MinHeap heap=new MinHeap(h1,0,n+1);//最小堆
//minOut[i]=顶点i的最小出边费用
float [] minOut=new float[n+1];
float minSum=0;//最小出边费用和
for(int i=1;i<=n;i++)
{//计算minOut[i]和minSum
float min=Float.MAX_VALUE;
for(int j=1;j<=n;j++)
if(a[i][j]>0 && a[i][j]
if(min==Float.MAX_VALUE) return Float.MAX_VALUE;//无回路
minOut[i]=min;
minSum+=min;
}
//各个变量初始化
int [ ]x=new int[n];
for(int i=0;i
float bestc=Float.MAX_VALUE;
//搜索排列树
while(enode!=null && enode.s
if(enode.s==n-2) //当前扩展结点是叶结点的父结点 ,再加2条边构成回路
//所构成回路是否优于当前最优解
{if(a[x[n-2]][x[n-1]]>0 && a[x[n-1]][1]>0 &&
enode.cc+a[x[n-2]][x[n-1]]+a[x[n-1]][1]
enode.cc=bestc;
enode.lcost=bestc;
enode.s++;
heap.insert(enode);
}
}
else
{ //产生当前扩展结点的儿子结点
for(int i=enode.s+1;i
{//可行儿子结点
float cc=enode.cc+a[x[enode.s]][x[i]];
float rcost=enode.rcost-minOut[x[enode.s]];
float b=cc+rcost;//最小费用下界
if(b
int []xx=new int[n];
for(int j=0;j
xx[i]=x[enode.s+1];
HeapNode node=new HeapNode(b,cc,rcost,enode.s+1,xx);
heap.insert(node);
}
}
}
//取下一扩展结点
enode=(HeapNode)heap.removemin();
}
x=enode.x;//将取得的最佳路线中最后一个结点的完整路线赋给x
for(int i=0;i
return bestc;
}
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
System.out.println("请输入地图的城市数:");
n=in.nextInt();
a=new float[n+1][n+1];
/*
* 例如:
* 0 30 6 4
30 0 5 10
6 5 0 20
4 10 20 0
又如:
0 5 4 6
5 0 3 7
4 3 0 12
6 7 12 0
*/
System.out.println("请输入地图的邻接矩阵:");
for(int i=1;i<5;i++) {
for(int j=1;j<5;j++) {
a[i][j]=in.nextFloat();
}
}
int[] v= {0,0,0,0,0};//最优路线
System.out.println(“最优路线花费和:”+bbTSP(v));
System.out.println(“最优路线:”);
for(int i=1;i<5;i++) {
System.out.print(v[i]+" ");
}
}
}
