从 递归 到 动态规划
暴力递归:自顶向下
1,把问题转化为规模缩小了的同类问题的子问题 ,要求 f(x) 必须求 f(y) ,进而必须求 f(z)…
2,有明确的不需要继续进行递归的条件(base case)
3,有当得到了子问题的结果之后的决策过程
4,不记录每一个子问题的解
动态规划:自底向上
1,从暴力递归中来
2,将每一个子问题的解记录下来,避免重复计算
3,把暴力递归的过程,抽象成了状态表达
4,从小到大,求出所有状态对应的值
动态规划的本质是递归加上缓存!
抽象描述:
一个系统,有若干状态,每个状态下有若干合法的操作,称为决策,决策会改变系统状态决策会带来收益(或费用)
在初始状态下,求最终状态下最大收益
在每个阶段,选择一些决策,状态随之改变
收益只取决与当前状态和决策(无后效性)——不是马尔可夫
使得系统达到终止状态时,总收益最大(或费用最小)
- 总收益一般指各阶段收益的总和
动态规划是在状态集合上的递推:f(new state)=f(old state)+payoff(decision)
是最短路:
图–广义有向无环图
- 节点:所有状态
- 边:可能的决策在状态上的转换
起点:初始状态
- 终点:终止状态
特点:
有 最优子结构
- 子问题最优决策可导出原问题最优决策
- 无后效性
有 重叠子问题
- 去冗余
- 空间换时间(加缓存)
问题共性:
- 套路
- 题中出现: 最优、最大、最小、最长、计数
- 是 离散问题
- 容易设计状态(如01背包问题)
- 最优子结构
- N-1 可以推导出 N
复杂度:
时间复杂度:O(状态数*每个状态下决策数)
空间复杂度:O(状态数)
解题步骤:
- 确定状态集合和收益
- 初始状态、终止状态
- 确定决策集合
- 是否无后效
- 收益如何表示
LeetCode 198 House Robber(打家劫舍)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
解法一:
分治、递归
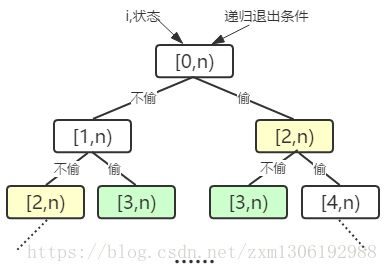
public int mydfs(int i,int[] nums) 函数表示从第 i 家开始偷,能得到的最大金额;
只考虑当前状态,
从第 i 家开始偷的最大金额
等于 第 i 家的金额+从第 i+2 家开始偷的最大金额 和
0+从第 i+1 家开始偷的最大金额(第i家不偷)
这两个数的最大值。
仅仅这样做会超时,需要将每次计算的状态加缓存,避免重复计算。如图可以看出会有重复的状态:
class Solution {
public static Map cache=new HashMap();
public int rob(int[] nums) {
if(nums.length<=0){
return 0;
}
cache.clear();
return mydfs(0,nums);
}
public int mydfs(int i,int[] nums){
if(i>=nums.length){
return 0;
}
if(cache.containsKey(i)){
return cache.get(i);
}
int a=nums[i]+mydfs(i+2,nums);
int b=0+mydfs(i+1,nums);
int c=Math.max(a,b);
cache.put(i,c);
return c;
}
} 解法二:
递归是自顶向下,将其改为自低向上推,非递归
状态为当前位置最大能偷多少钱,所以最后一个位置,最大能偷的钱数就是最后一家的钱数。
class Solution {
public static Map cache=new HashMap();
public int rob(int[] nums) {
if(nums.length<=0){
return 0;
}
cache.clear();
int n=nums.length;
cache.put(n-1,nums[n-1]);
for(int i=n-2;i>=0;i--){
int a=nums[i]+(cache.containsKey(i+2)?cache.get(i+2):0);
int b=0+(cache.containsKey(i+1)?cache.get(i+1):0);
cache.put(i,Math.max(a,b));
}
return cache.get(0);
}
} 状态标记 i 永远是[0,n-1) 所以可以用数据存,用数组存比Map省空间:
class Solution {
public static int[] cache=new int[10000];
public int rob(int[] nums) {
if(nums.length<=0){
return 0;
}
int n=nums.length;
cache[n-1]=nums[n-1];
for(int i=n-2;i>=0;i--){
int a=nums[i]+(i+22]:0);
int b=0+( i+11]:0);
cache[i]=Math.max(a,b);
}
return cache[0];
}
} 继续修改上面的代码:
1:增加特判->可能减少耗时;
2:精简代码。发现只有i=n-2是,i+2才不会小于n ,三元表达式后面都是多余的。增加cache[n-2] 的计算,后面就不用判断边界了,三行代码可以减为一行。
class Solution {
public static int[] cache=new int[10000];
public int rob(int[] nums) {
if(nums.length<=0){
return 0;
}
if(nums.length==1){
return nums[0];
}
int n=nums.length;
cache[n-1]=nums[n-1];
cache[n-2]=Math.max(nums[n-2],nums[n-1]);
for(int i=n-3;i>=0;i--){
cache[i]=Math.max(0+cache[i+1],nums[i]+cache[i+2]);
}
return cache[0];
}
}小兵向前冲
参考:https://blog.csdn.net/fan2012huan/article/details/52514789
N*M的棋盘上,小兵要从左下角走到右上角,只能向上或者向右走,问有多少种走法?
注意:N*M 的棋盘,N和M为格子数,坐标一共有 (N+1)*(M+1) 个,小兵起始坐标为(0,0)终点坐标为(N,M)。
套路:是计数问题
这道题的状态是二维的。
递归:自顶向下
其实这是一个数学的组合问题:
从左下角走到右上角总共只需要走8步(要么向右走4步,要么向上走4步),这样只需要C(8,4)就可以了。
递归代码:
从终点往起点推。
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 4;
private static final int M = 4;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
result[i][j] = -1;
}
}
System.out.println(search(N, M));
}
public static int search(int xi, int yi) {
if (xi == 0 || yi == 0) {
return 1;
}
// 缓存
if (result[xi][yi] >= 0) {
return result[xi][yi];
}
result[xi][yi] = search(xi - 1, yi) + search(xi, yi - 1);
return result[xi][yi];
}
}递归实现:
自低向上
从起点往终点推。
状态 result[i][j] 为到达坐标 (i,j) ,有几种走法。
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 4;
private static final int M = 4;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for(int i=0;i<=N;i++){
result[i][0]=1;//到达坐标(x,0)只有一种走法,即向上
}
for(int j=0;j<=M;j++){
result[0][j]=1;//到达坐标(0,x) 只有一种走法,即向左
}
//递推
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
result[i][j]=result[i-1][j]+result[i][j-1];//到达坐标(i,j)的走法=到达(i-1,j)的走法+到达(i,j-1)的走法
}
}
System.out.println(result[N][M]);
}
}小兵先前冲,某点不能走
先用数学分析下:
记(0,0)点为A点,(7,5)点为B点,(3,3)点为P点。
从A->B点总共C(12,5)种走法。
从A->P点总共C(6,3)种走法。
从P->B点总共C(6,2)种走法。
由于P点不能走,那么经过P点,从A点走到B点有几种走法呢?
C(6,3)*C(6,2)种走法。
因此,不经过P点的走法:C(12,5)-C(6,3)*C(6,2)=492种走法。
注意,这个结果跟不经过哪个点有直接关系。
比如现在改为(2,2)点不能走,则:
C(12,5)-C(4,2)*C(8,3)=456种。
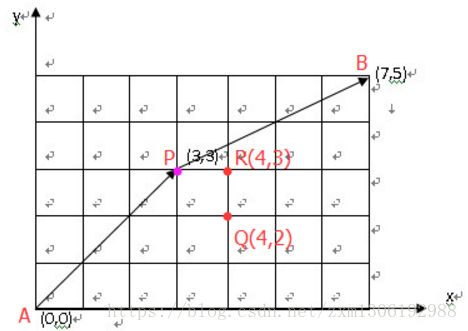
要到达R点需要经过P点和Q点,这时P不能走,则只需要置为0即可。即:search(4,3) = 0 + search(4,2);
也就是说,遇到(3,3)这个点就返回0。
在上题基础上增加判断条件即可。
递归:
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 7;
private static final int M = 5;
//(XNO,YNO)这个点表示不能走
private static final int XNO = 3;
private static final int YNO = 3;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
result[i][j] = -1;
}
}
System.out.println(search(N, M));
}
public static int search(int xi, int yi) {
if (xi == 0 || yi == 0) {
return 1;
}
//(XNO,YNO)这个点表示不能走
if (xi == XNO && yi == YNO) {
return 0;
}
// 缓存
if (result[xi][yi] >= 0) {
return result[xi][yi];
}
result[xi][yi] = search(xi - 1, yi) + search(xi, yi - 1);
return result[xi][yi];
}
}递推:
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 7;
private static final int M = 5;
//(XNO,YNO)这个点表示不能走
private static final int XNO = 3;
private static final int YNO = 3;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for(int i=0;i<=N;i++){
result[i][0]=1;//到达坐标(x,0)只有一种走法,即向上
}
for(int j=0;j<=M;j++){
result[0][j]=1;//到达坐标(0,x) 只有一种走法,即向左
}
//递推
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
//(XNO,YNO)这个点表示不能走
if (i == XNO && j == YNO) {
result[XNO][YNO] = 0;
} else {
result[i][j]=result[i-1][j]+result[i][j-1];//到达坐标(i,j)的走法=到达(i-1,j)的走法+到达(i,j-1)的走法
}
}
}
System.out.println(result[N][M]);
}
}小兵向前冲,往上、右可以走1步或两步
只要后面增加两项即可:
到达坐标 (i,j) 的走法数,result[i][j] ,等于到达左边一格的走法数 result[i-1][j] + 到达下面一格的走法数 result[i][j-1]+达到左边二格的走法数 result[i-2][j] + 到达下面二格的走法数 result[i][j-2]。
这次由于-2,递归时,xi,yi 可能跳过0,直接为负数,所以要增加递归退出条件。
递归:
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 2;
private static final int M = 2;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
result[i][j] = -1;
}
}
System.out.println(search(N, M));
}
public static int search(int xi, int yi) {
if (xi == 0 || yi == 0) {
return 1;
}
if (xi < 0 || yi < 0) {
return 0;
}
// 缓存
if (result[xi][yi] >= 0) {
return result[xi][yi];
}
result[xi][yi] = search(xi - 1, yi) + search(xi, yi - 1)+ search(xi-2, yi) + search(xi, yi-2);
return result[xi][yi];
}
}递推:
需要先递推出,第一行、第二行、第一列,第二列,防止推中间坐标时,越界。
递推要比递归难写。因为要考虑很多特殊情况。最常见的就是,数组下标不要出现负数以及不要越界。这样,对于使得数组下标出现负数的情况,需要特殊赋初值。
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 2;
private static final int M = 2;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
//推出第一列
for(int i=0;i<=N;i++){
result[i][0]=1;//到达坐标(x,0)只有一种走法,即向上
}
//推出第一行
for(int j=0;j<=M;j++){
result[0][j]=1;//到达坐标(0,x) 只有一种走法,即向左
}
result[1][1] = result[0][1] + result[1][0];
//推出第二列
for (int i = 2; i <= N; i++) {
result[i][1] = result[i-1][1] + result[i][0] + result[i-2][1];
}
//推出第二行
for (int j = 2; j <= M; j++) {
result[1][j] = result[1][j-1] + result[0][j] + result[1][j-2];
}
//递推
for(int i=2;i<=N;i++){
for(int j=2;j<=M;j++){
result[i][j]=result[i-1][j]+result[i][j-1]+ result[i-2][j] + result[i][j-2];//到达坐标(i,j)的走法=到达(i-1,j)的走法+到达(i,j-1)的走法+到达(i-2,j)的走法+到达(i,j-2)的走法
}
}
System.out.println(result[N][M]);
}
}组合 个数问题
从n个东西里去m个:
C(n,m) = C(n-1, m-1) + C(n-1, m)
C(n-1, m-1)表示第n个东西被选了
C(n-1, m)表示第n个东西没有被选
递归:
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 20;
private static final int M = 10;
private static int[][] result;
public static void main(String[] args) {
result = new int[N + 1][M + 1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
result[i][j] = -1;
}
}
System.out.println(search(N, M));
}
public static int search(int n, int m) {
if (nreturn 0;
}
if (m==0) {
return 1;
}
// 缓存
if (result[n][m] >= 0) {
return result[n][m];
}
result[n][m] = search(n - 1, m-1) + search(n-1, m);
return result[n][m];
}
} 递推:
public class Main {
// 定义x轴有N个格子,y轴有M个格子
private static final int N = 20;
private static final int M = 10;
private static int[][] result;
public static void main(String[] args) {
result = new int[N+1][M+1];
for(int i=0;i<=N;i++){
for(int j=0;j<=M;j++){
if(i==j||j==0){
result[i][j]=1;
}
if(i0;
}
}
}
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
result[i][j]=result[i-1][j-1]+result[i-1][j];
}
}
System.out.println(result[N][M]);
}
} 01背包问题
小偷有一个容量为W的背包,有n件物品,第i个物品价值vi,且重wi
目标: 找到xi使得对于所有的xi = {0, 1}
sum(wi*xi) <= W, 并且 sum(xi*vi)最大
套路:最大
递归:
public class Main2 {
static int n;
static int c;
static int[] weight;
static int[] price;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("输入物品数量n:");
n = sc.nextInt();
System.out.println("输入背包容量c:");
c = sc.nextInt();
System.out.println("输入" + n + "个物品的重量:");
weight = new int[n];
for (int i = 0; i < n; i++) {
weight[i] = sc.nextInt();
}
System.out.println("输入" + n + "个物品的价值:");
price = new int[n];
for (int i = 0; i < n; i++) {
price[i] = sc.nextInt();
}
System.out.println(robot(0, c));
}
static Map cache = new HashMap();
private static int robot(int idx, int w) {// idx表示从第i个物品开始取,w为背包剩余容量,这两个可以构成一个状态
if (idx >= n || w- weight[idx] <= 0) {//背包装不下第idx个物品了直接返回
return 0;
}
if (cache.containsKey(new Pair(idx, w))) {
return cache.get(new Pair(idx, w));
}
int a = robot(idx + 1, w - weight[idx]) + price[idx];
int b = robot(idx + 1, w);
int c = Math.max(a, b);
cache.put(new Pair(idx, w), c);
return c;
}
}
class Pair {
int idx;
int w;
Pair(int i, int ww) {
this.idx = i;
this.w = ww;
}
} 时间空间复杂度都是 O(n*w)
递推:
public class Main2 {
static int n;
static int c;
static int[] weight;
static int[] price;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("输入物品数量n:");
n = sc.nextInt();
System.out.println("输入背包容量c:");
c = sc.nextInt();
System.out.println("输入" + n + "个物品的重量:");
weight = new int[n];
for (int i = 0; i < n; i++) {
weight[i] = sc.nextInt();
}
System.out.println("输入" + n + "个物品的价值:");
price = new int[n];
for (int i = 0; i < n; i++) {
price[i] = sc.nextInt();
}
cache=new int[n][c+1];
for(int i=n-1;i>=0;--i){
for(int w=0;w<=c;++w){
cache[i][w]=Math.max( check(i+1,w-weight[i])+price[i] , check(i+1,w) );
}
}
System.out.println(cache[0][c]);
}
static int[][] cache;
private static int check(int idx,int w){
if (idx >= n || w- weight[idx] <= 0) {//背包装不下第idx个物品了直接返回
return 0;
}
return cache[idx][w];
}
}如果 W很多怎么办,cache消耗的空间太大了
空间和时间的区别:时间消耗就消耗 了,空间可以重复利用
发现 循环中,每次cache数组,i 只和 i+1 有关系,所以可以cache数组横坐标只用申请前2个空间,每次取和放的时候,横坐标都模2,使得空间可以重复利用,空间复杂度变为 O(W)
这个技巧叫滚动数组
public class Main2 {
static int n;
static int c;
static int[] weight;
static int[] price;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("输入物品数量n:");
n = sc.nextInt();
System.out.println("输入背包容量c:");
c = sc.nextInt();
System.out.println("输入" + n + "个物品的重量:");
weight = new int[n];
for (int i = 0; i < n; i++) {
weight[i] = sc.nextInt();
}
System.out.println("输入" + n + "个物品的价值:");
price = new int[n];
for (int i = 0; i < n; i++) {
price[i] = sc.nextInt();
}
cache=new int[2][c+1];
for(int i=n-1;i>=0;--i){
for(int w=0;w<=c;++w){
cache[i%2][w]=Math.max( check(i+1,w-weight[i])+price[i] , check(i+1,w) );
}
}
System.out.println(cache[0][c]);
}
static int[][] cache;
private static int check(int idx,int w){
if (idx >= n || w- weight[idx] <= 0) {//背包装不下第idx个物品了直接返回
return 0;
}
return cache[idx%2][w];
}
}上边为只需要输出最大价值,如果需要输出装哪些物品,见:https://blog.csdn.net/zxm1306192988/article/details/80582672
最大公共子序列
https://blog.csdn.net/zxm1306192988/article/details/72835759
旅行商问题
确定状态:f(s,x)表示经过s集合里那些城市,最终在城市x时所经过的最小距离。s表示经历过的城市集合;X表示最后一个城市,在集合s里
初始状态: f({1},1) = 0,假设从城市1开始
终止状态:f({1,2,3,..n},1)=?
决策: 在状态(s, x)找到一个不在集合s里的城市y,若从x走到y,则f(s,x) + distance(x,y)是一个经过集合sUy城市的路径。
无后效性:收益只取决于状态(s,x)和决策y
费用表示: f(s,x) = min {f(s – x, y) + distance(y,x) }其中s-x表示从集合s中去掉城市x之后的集合, y在集合s-x中
注意点: 最后回到起点的状态有点特殊,因为起点已经在集合里
复杂度:集合数 2n 2 n , 状态数 2n*n 2 n * n
时间复杂度 :枚举s, x, y,所以总复杂度 O(2n*n2) O ( 2 n * n 2 )
空间复杂度: O(2n*n) O ( 2 n * n )
用set 表示集合效率较低。如果要保存的数都是不重复的比较小的整数,可以用二进制串表示。
如集合{1,3,5,6,7} 表示成二进制串用 1110101 ,其中集合里面有的数对应的位数写成1,没有的写成0。
要判断第3位是不是1,就把 1110101 右移(3-1)位,得到11101,然后和 00001 &,如果结果为1 表示集合中有3,否则表示集合中没有3。
推广一下,对于数字x,要看它的第i位是不是1,那么可以通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现。
递归实现:
https://blog.csdn.net/hu413031273/article/details/51329514
非递归:
https://www.cnblogs.com/youmuchen/p/6879579.html
总结
套路:滚动数组、状态压缩、升维、单调性、四边形不等式(高级套路)
本质:先暴力,找冗余,去冗余