线段树详解-延迟标记-BIT
1.线段树是什么?
线段树是一种特殊的数据结构,一般表现为自定义结构体构建出的一个二叉树或者一个数组存储的二叉树.
2.线段树有什么用?
一般用于解决这种问题:
区间状态的更新查询问题,
标志性经典问题:
1.RMQ问题:
对于长度为n的数列A,修改第i个元素为x,并要求即时回答若干询问RMQ(A,i,j)(i,j<=n),返回数列A中下标在i,j区间里的最小(大)值
2.区间和问题
对于长度为n的数列A,修改第i个元素为x,并要求即时回答若干询问i,j(i,j<=n),返回数列A中下标在i,j区间里的区间和
3.线段树实现思路
(1).什么是记忆化
还记得记忆化数组的思维吧?
记录曾经计算出的结果,在之后的计算里直接使用之前的结果以避免重复的计算,从而达到高效.
(2).线段树做的"记忆化"
来,我给你讲一个笑话,针对n个数字的数组a,我们预处理出一个n*n大小的二维数组memory[n][n],memory[i][j]存的就是数组中[i,j]范围内的最小值,这样我们回答任何一个[i,j]内最小值为多少的问题时只需要O1的复杂度就行了,快吧?
很愚蠢,为什么呢,一方面这个数组在n很大的时候会爆空间,一方面预处理这个数组里n*n个数据无论什么算法时间都会爆,那我们优化一下呢,也许我们不要想O1一步登天就好了,Ologn好像还不错,看下图:
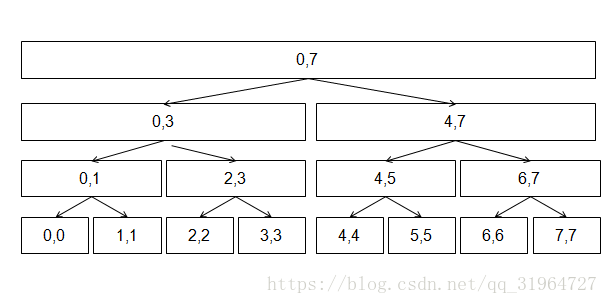
[0,0]的最小值就是a[0],[1,1]的最小值就是a[1],[2,2]的最小值是a[2],也就是最底层的我们是知道的,由底向上按层计算每个节点直接比较取两个子节点的最小值就好了,故而预处理出这个树只需要n的复杂度而已,那我们思考查询功能,对于容易一个区间[i,j],我们必定可以将之分解为将近logn个已求解答案的区间,比如[0,6]可以被我们分解为树中的[0,3]+[4,5]+[6,6],比较这三个结点的最小值就好了.
预处理出这么n个数据然后以均摊logn的复杂度解决任意区间[i,j]的最小值查询,这就是线段树的"记忆化".
我们发现树中每个结点存储的数据其实都是一段区间的数据计算结果,区间就好像一条条或或短的线段,这是线段树这个名字的来源.
(3).RMQ模版
#include
#include
const int maxn=10000;
const int inf=(1<<30);
int n;
int dat[4*maxn];
int min(int a,int b){ return a0){
k=(k-1)>>1;
dat[k]=min(dat[(k<<1)+1],dat[(k<<1)+2]);
}
}
void init(int tn){//采用先重置n为w的幂次数并全部填充inf保证树最开始是正确的,然后在更新n个初始数字
n=1;
while(nr||b=r) return dat[k]; //是答案区间的一部分,返回值
else{ //一部分是一部分不是就继续递归
int v1=query(a,b,(k<<1)+1,l,(l+r)>>1);
int v2=query(a,b,(k<<1)+2,((l+r)>>1)+1,r);
return min(v1,v2);
}
}
int main(){
scanf("%d",&n);
init(n);
while(1){
fflush(stdin);
printf("输入命令:");
int t1,t2;
char ch;
scanf("%c%d%d",&ch,&t1,&t2);
if(ch=='Q') printf("%d\n",query(t1,t2,0,1,n));
else if(ch=='U') update(t1,t2);
getchar();
}
return 0;
} (3).对于区间求和问题
如果我们的问题不是区间最小值而是区间求和怎么办?
之前RMQ问题中每个结点存的数据是本区间的最小值,其实只要把每个结点的数据改为本区间的数据和就好了.就好像查询[0,6]区间的区间和,可以将[0,6]分解为树中的[0,3]+[4,5]+[6,6],将这三个结点数据相加就是[0,6]的区间和.
由此思路将RMQ的代码小改一下:
#include
#include
const int maxn=10000;
const int inf=(1<<30);
int n;
int dat[4*maxn];
int min(int a,int b){ return a0){
k=(k-1)>>1;
dat[k]=dat[(k<<1)+1]+dat[(k<<1)+2]; //改为加
}
}
void init(int tn){//采用先重置n为w的幂次数并全部填充0保证树最开始是正确的,然后在更新n个初始数字
n=1;
while(nr||b=r) return dat[k]; //是答案区间的一部分,返回值
else{ //一部分是一部分不是就继续递归
int v1=query(a,b,(k<<1)+1,l,(l+r)>>1);
int v2=query(a,b,(k<<1)+2,((l+r)>>1)+1,r);
return v1+v2; //改为了加
}
}
int main(){
scanf("%d",&n);
init(n);
while(1){
fflush(stdin);
printf("输入命令:");
int t1,t2;
char ch;
scanf("%c%d%d",&ch,&t1,&t2);
if(ch=='Q') printf("%d\n",query(t1,t2,0,1,n));
else if(ch=='U') update(t1,t2);
getchar();
}
return 0;
} 然而很明显上面这个只能对单个数组数字进行更新,如果我们要做的是对一个区间内的数都加减某个值,依然用这种思路就会为n*logn的更新复杂度,此时我们需要用到一种思维:延迟更新:
(4).延迟更新
我们可以对于每个结点增加一个属性:int add;
add记录的是此节点所代表的区间所有数被加的值
也就是当我们要做[0,6]所有数加3这种更新时,我们并没有更新树中对应结点的value,而是去更新[0,3]+[4,5]+[6,6]这三个结点的add,使之+3便可,这样我们就用logn完成了区间更新,相对的因为我们只是更新了add,故而做查询时需要将上面的add向下面传导,不过我们这样做就只用传导需要用到的那部分区间的add,大大节约了时间.
//线段树的区间更新(延迟标记)
#include
#include
using namespace std;
const int maxn=100000;
int n,a,b,dat[4*maxn],add[4*maxn],temp;
void init(int tn){
n=1;
while(n>1+1;
add[k<<1|1]+=add[k];
dat[k<<1|1]+=temp*add[k];
add[(k+1)<<1]+=add[k];
dat[(k+1)<<1]+=temp*add[k];
add[k]=0;
}
void update(int k,int l,int r,int val){ //对[a,b]区间内每个数加val,k传0,l传1,r传n
if(rb) return ;
if(r<=b&&l>=a){
dat[k]+=val*(r-l+1);
add[k]+=val;
return ;
}
update((k<<1)+1,l,l+r>>1,val);
update(k+1<<1,(l+r>>1)+1,r,val);
}
int query(int k,int l,int r){
if(rb) return 0;
if(r<=b&&l>=a) return dat[k];
if(add[k]) pushdown(k,l,r); //对于add的向下传递
return query((k<<1)+1,l,l+r>>1)+query(k+1<<1,(l+r>>1)+1,r);
}
int main(){
int m;
scanf("%d%d",&n,&m);
int tn=n;
init(n);
for(int i=1;i<=tn;i++){
scanf("%d",&temp);
int k=i+n-2;
dat[k]=temp;
while(k>0){
k=(k-1)>>1;
dat[k]=dat[(k<<1)+1]+dat[(k+1)<<1];
}
}
for(int i=0;i (5).区间求和问题的更优处理-BIT
有点难解释,待添加
//树状数组BIT
/*
作用:
1.给定i计算1到i的和
2.给定i和x,执行ai+=x;
*/
#include
#include
#include
using namespace std;
const int maxn=10000;
int bit[maxn+1],n;
int sum(int i){
int s=0;
while(i>0){
s+=bit[i];
i-=i&-i;
}
return s;
}
void add(int i,int x){
while(i<=n){
bit[i]+=x;
i+=i&-i;
}
}
void init(int tn){
n=1;
while(n