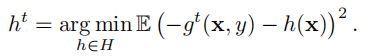【论文笔记】CatBoost: unbiased boosting with categorical features
原论文地址:here,本文主要记录论文中重要的部分。
1. Abstract
CatBoost 中最主要的两个算法性的特点在于:实现了有序提升,排列驱动以代替经典算法;一种新颖的算法处理分类变量。这些方法旨在解决prediction shift(普遍存在于梯度提升算法中)。
2. Introduction
所有现存的梯度提升算法都存在统计学上的问题。经过多次提升的预测模型 F F F 依赖于训练样本的目标变量的。我们论证了:这会导致来自训练样本中 X k X_k Xk 的 F ( X k ) ∣ X k F(X_k)|X_k F(Xk)∣Xk 分布与测试样本中 X X X 的 F ( X k ) ∣ X k F(X_k)|X_k F(Xk)∣Xk 分布的偏移。这最终会导致训练模型的prediction shift。我们将这种的问题称作:target leakage。
3. Categorical features
一种有效的处理分类特征的方法就是:使用一个计算出的数值(target statistic (TS))来代替 x k i x_k^{i} xki (表示第k个训练样本的第i个分类型特征)。这个数值TS计算如下: x ^ k i = E ( y ∣ x i = x k i ) \hat x_k^{i}=E(y|x^i=x_k^i) x^ki=E(y∣xi=xki)。
3.1 Greedy TS
由于某些类别出现次数少,所以需要做平滑处理:
x ^ k i = ∑ j = 1 n I { x j i = x k i } ⋅ y j + a P ∑ j = 1 n I { x j i = x k i } + a \hat x_k^{i}=\frac{\sum_{j=1}^{n}I_{\{x_j^i=x_k^i\}}\cdot y_j+aP}{\sum_{j=1}^{n}I_{\{x_j^i=x_k^i\}}+a} x^ki=∑j=1nI{xji=xki}+a∑j=1nI{xji=xki}⋅yj+aP
其中,函数 I I I为指示函数,满足 { x j i = x k i } {\{x_j^i=x_k^i\}} {xji=xki}条件则函数值取1,否则函数值取0。
a > 0 a>0 a>0为参数, P P P通常取作所有数据中目标变量的平均值。但是,这样的平滑处理可能造成一个问题,也就是target leakage: E ( x ^ i ∣ y = v ) = E ( x ^ k i ∣ y k = v ) E(\hat x^i|y = v) = E(\hat x_k^i|y_k = v) E(x^i∣y=v)=E(x^ki∣yk=v),这个式子可能不成立。
注:博主还没弄清楚为什么Greedy TS会存在这个问题,待更新。。
大概懂了,意思就是:假设某个分类变量没有重复值,即每个样本对应一个分类值,这样的话,计算 E ( x ^ k i ∣ y k ) = y k + a P 1 + a E(\hat x_k^i|y_k) = \frac{y_k+aP}{1+a} E(x^ki∣yk)=1+ayk+aP,而计算 E ( x ^ i ∣ y ) = P E(\hat x^i|y) =P E(x^i∣y)=P,也就说对单个样本的估计量是有偏的。作为参考对比,可以考虑均值估计方法,就是无偏的估计方法。
所以,需要解决办法之一就是使用除去 x k x_k xk 样本的数据子集来估计 x k i x_k^i xki 的值: D k ⊂ D − { x k } D_k \subset D- \{x_k\} Dk⊂D−{xk},而不是使用全体数据集 D D D。
3.2 Ordered TS
CatBoost使用更加有效的处理方式。使用次序原则(ordering principle,文章的核心思想),这受在线学习算法的启发(在线学习算法按照时序来获取训练数据)。简单地说,就是TS值的计算依靠目前已经观察的样本集。我们可以随机生成一个排列来实现带时序的训练集,CatBoost在不同的梯度提升步中使用不同的排列。
4. Prediction shift and ordered boosting
同样,在每一步的梯度提升的过程中,也存在 prediction shift 的问题,它是由某种特殊类型的target leakage造成的,处理方法类似于Ordered TS。
梯度提升算法中,在提升步做法如下式(1)( h t h^t ht 为新生成的弱分类器, − g t ( x k , y k ) -g^t(x_k, y_k) −gt(xk,yk) 为损失函数在当前模型下的负梯度,即为弱分类器要拟合的值):
h t = a r g m i n { h ∈ H } 1 n ∑ k = 1 n ( − g t ( x k , y k ) − h ( x k ) ) h_t=argmin_{\{h\in H\}}\frac{1}{n}\sum_{k=1}^{n}(-g^t(x_k, y_k)-h(x_k)) ht=argmin{h∈H}n1k=1∑n(−gt(xk,yk)−h(xk))
链式偏移可以描述如下:
- 梯度的条件分布 g t ( x k , y k ) ∣ x k g_t(x_k, y_k) | x_k gt(xk,yk)∣xk 与训练样本 g t ( x , y ) ∣ x g_t(x, y) | x gt(x,y)∣x 分布存在偏移;
- 从而, h t h^t ht 的估计式(1)也会与式(2)存在偏差。
- 最终,会影响模型 F t F^t Ft的泛化能力。
4.1 prediction shift 举例
在一般的回归问题中,损失函数为 L ( y , y ^ ) = ( y − y ^ ) 2 L(y, \hat y)=(y-\hat y)^2 L(y,y^)=(y−y^)2。此时,负梯度 − g t ( x k , y k ) = y k − F t − 1 ( x k ) -g^t(x_k, y_k)=y_k - F^{t-1}(x_k) −gt(xk,yk)=yk−Ft−1(xk),恰好等于每个样本的残差。
假设有两个变量 x 1 , x 2 x^1, x^2 x1,x2 独立同服从伯努利分布(p=0.5),且 y = f ∗ ( x ) = c 1 x 1 + c 2 x 2 y=f^*(x) =c_1x^1+c_2x^2 y=f∗(x)=c1x1+c2x2。经过两次梯度提升的迭代后,我们得到模型 F = F 2 = h 1 + h 2 F=F^2=h^1+h^2 F=F2=h1+h2,假设 h 1 h^1 h1基于变量 x 1 x^1 x1, h 2 h^2 h2基于变量 x 2 x^2 x2。
有以下定理(具体证明见原论文):
- 如果大小为 n n n的两个独立样本 D 1 D_1 D1和 D 2 D_2 D2被分别用来估计 h 1 h^1 h1 和 h 2 h^2 h2,使用式(1),有 E D 1 , D 2 F 2 ( x ) = f ∗ ( x ) + O ( 1 / 2 n ) E_{D_1,D_2}F^2(x)=f^*(x) + O(1/2^n) ED1,D2F2(x)=f∗(x)+O(1/2n),对任意 x ∈ { 0 , 1 } 2 x\in\{0,1\}^2 x∈{0,1}2。
- 如果相同的数据集 D = D 1 = D 2 D=D_1=D_2 D=D1=D2 均用于 h 1 h^1 h1和 h 2 h^2 h2,则 E D F 2 ( x ) = f ∗ ( x ) − 1 n − 1 c 2 ( x 2 − 1 2 ) + O ( 1 / 2 n ) E_DF^2(x)=f^*(x)-\frac{1}{n-1}c_2(x^2-\frac{1}{2})+O(1/2^n) EDF2(x)=f∗(x)−n−11c2(x2−21)+O(1/2n).
上面的理论告诉我们,如果在每次迭代提升步,使用相互独立的数据集,则得到的训练模型是对原有模型 f ∗ ( x ) f^*(x) f∗(x) 的无偏估计。否则,使用相同的数据集,则会得到有偏估计的模型,且数据集越大,偏差越小。
4.2 Ordered boosting
为了解决上述提到的 prediction shift,方法如下:
- 首先随机生成一个 1 − n 1-n 1−n的排列 σ \sigma σ
- 维护 n n n 个不同的 supporting models M 1 , . . . , M n M_1,...,M_n M1,...,Mn,使得 M i M_i Mi是仅利用了排列中的前 i i i个样本得到的训练模型。
- 迭代的每一步,为了得到第 j j j个样本残差的估计值,使用模型 M j − 1 M_{j-1} Mj−1 估计。
事实上,由于上述方法需要维护 n n n个不同的模型,所以导致时间和空间复杂度都比较高。在CatBoost中,使用了改进的GBDT。
5. Practical implementation
下面从各个方面给出算法细节:
5.1 Building a tree
CatBoost 使用决策树,每次分裂节点均使用相同的策略。由【Algorithm.2】,在Ordered Mode下,在计算梯度或者计算某个叶子节点平均梯度值,均只利用前 i i i 个样本的信息。而在Plain Mode下,流程和GBDT算法类似,但是对于分类变量,计算其TS时仍会使用带permutation的模式(使用随机排列 σ 0 \sigma^0 σ0)。
5.2 Choosing leaf values
在所有树结构都建立好的情况下,最终模型 F F F 的叶子节点值是通过标准的梯度提升处理得到的,对于分类变量就需要使用随机排列 σ o \sigma^o σo 计算TS值。
5.3 Complexity
5.4 Feature combinations
CatBoost另外一个重要的细节就是对TS使用特征结合,它能捕捉高阶的依赖信息。但是特征结合数目呈指数级增长,所以考虑所有特征组合不太现实。
CatBoost贪心地构造特征组合。每一次进行下一次树节点的分裂时,CatBoost结合当前树上已经使用的分类型变量和数据集中所有的分类型变量。新的组合变量在运行中转换为TS。