关于线段树区间修改lazy标记的理解

正常对点的修改是不需要lazy标记的因为对于一个点来说他不存在子区间，因而在更新的时候自然就会直接找到，比如说点为a，最后到达的区间就是[a,a],而对于区间修改，我们到达的某一个子区间，那么对于他的每一个子区间，其本身的值就不会出现太大改变，这里是我最初步理解的地方，在b站看了点视频讲解之后理解了，这要是理解了，线段树算是出入门了，其实理解了之后还是不太难的，而且这是一种很好用的数据结构，比树状数组应用范围广很多，可以说树状数组能解决的一般它都能解决，而且以后就会发现线段树的强大之处，在这里举个例题(模板题）。

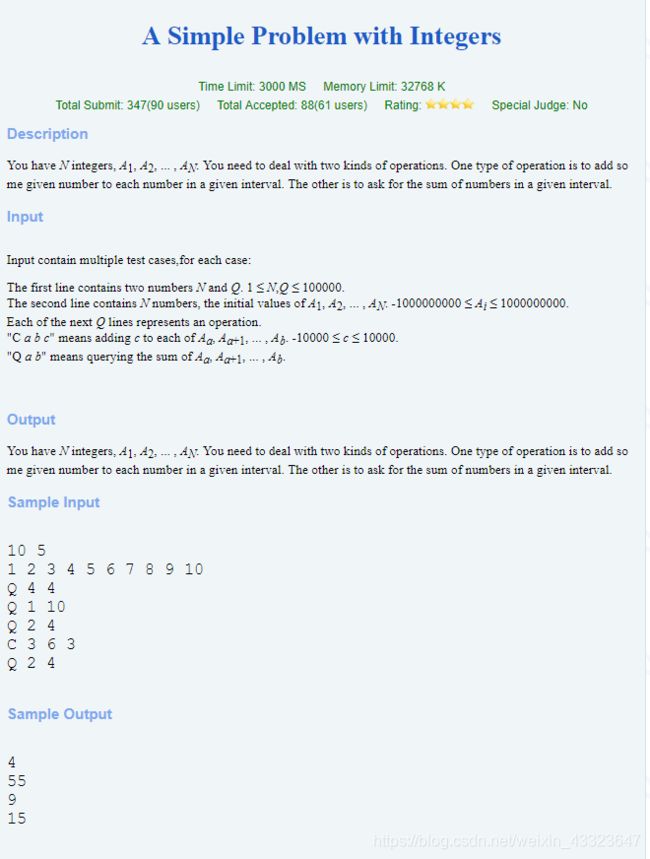
这里题意很简单，大家可以试着去翻译一下，就是C是对区间[a,b]加上c，Q就是求[a,b]的和。

#include 
typedef long long ll;
#define pb push_back
#define db double
#define lson l,m,rt*2
#define rson m+1,r,rt*2+1
ll a[100005];
ll tree[400050];
ll flag[400050];
using namespace std;
void pushup(int rt)
{
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
}
void pushdown(int l,int r,int rt)
{
    if(flag[rt])
    {
        int m = (l+r)>>1;
        flag[rt*2] +=flag[rt];
        flag[rt*2+1] += flag[rt];
        tree[rt*2]+=(m - l + 1)*flag[rt];
        tree[rt*2+1]+=(r-m)*flag[rt];
        flag[rt] = 0;//这里就是你把你的lazy标记传给节点你就要恢复初始状态。
    }
}
void build(int l,int r,int rt)
{
    if(l == r)
    {
        tree[rt] = a[l];
        flag[rt] = 0;
    }
    else
    {
        int m = (l+r)>>1;
        build(lson);
        build(rson);
        pushup(rt);
    }
}
void update(int L,int R,int c,int l,int r,int rt)
{
    if(L <= l&& r <= R)
    {
        tree[rt]+=(c*(r-l+1));
        flag[rt]+=c;
        return ;
    }
    pushdown(l,r,rt);
    int m = (l+r)>>1;
    if(L <= m)
    {
        update(L,R,c,lson);
    }
    if(R > m)
    {
         update(L,R,c,rson);
    }
    pushup(rt);
}
ll query(int L,int R,int l,int r,int rt)
{
    if(L <= l && r <= R)
    {
        return tree[rt];
    }
    else
    {
        pushdown(l,r,rt);//注意这里pushdown的原因是在更新区间的时候可能还有lazy已经标记完的区间没有向下传递，因而对于所求区间还是要pushdown一下的。
        ll ans = 0;
        int m = (l+r)>>1;
        if(L <= m)
        {
            ans+=query(L,R,lson);
        }
        if(R > m)
        {
            ans+=query(L,R,rson);
        }
        return ans;
    }
}
int main()
{
    int n,q;
    while(~scanf("%d%d",&n,&q))
    {
        memset(flag,0,sizeof(flag));
        memset(tree,0,sizeof(tree));
        for(int i = 1;i <= n;i++)
        {
            scanf("%d",&a[i]);
        }
        build(1,n,1);
        char op[2];
        for(int i = 1;i <= q;i++)
        {
            scanf("%s",op);
            if(op[0] == 'Q')
            {
                int a,b;
                scanf("%d%d",&a,&b);
                printf("%d\n",query(a,b,1,n,1));
            }
            if(op[0] == 'C')
            {
                int a,b,c;
                scanf("%d%d%d",&a,&b,&c);
                update(a,b,c,1,n,1);
            }
        }
    }
}