【Python】KMP算法

字符串查找问题

给定文本串text和模式串pattern，从文本串text中找出模式串pattern第一次出现的位置。

暴力求解算法

Python代码

# 暴力求解
def brute_force_search(ss, s):
    i = 0  # 当前匹配的原始字符串首位
    j = 0  # 模式串的匹配位置
    size = len(s)
    nlast = len(ss) - size
    while i <= nlast and j < size:
        if ss[i + j] == s[j]:  # 若匹配模式串位置后移
            j += 1
        else:  # 若不匹配，则对比下一个位置，模式串回溯到首位
            i += 1
            j = 0
    if j >= size:
        return i
    return -1

暴力求解的思路比较简单，这里就不在赘述。

---

KMP算法

当暴力求解不匹配的时候，每次都要再一次从模式串首位做匹配，如下图， x ! = y 时，每次右移1位，然后从头比较：

其实虚线中的移动都是多余的，直接移动到c所在的位置，比较c和x是否相等就可以了。所以关键是怎么在y求c所在的位置。观察模式串：

c 所在的位置就是 y 前面的字符串的最大相同前缀(ab)和后缀(ab)的数量 2 ，令 y 的next为2。
如果能把所有位置的next值都能够求出来，比较的时候，当字符不匹配时，模式串直接移动到next标识的位置，然后继续比较就可以了。这就是KMP算法。

求next就是求字符串的最大相等前缀和后缀：

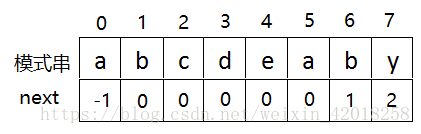
如：j=7时，考察字符串“abcdeab”的最大相等k前缀和k后缀：

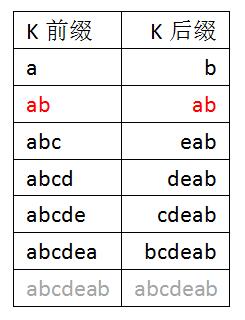
字符串“abcdeab”的最大相等k前缀和k后缀是"ab"，值为2。
计算 next[ j ] 时，考察的字符串是模式串的前 j - 1 个字符，求其中最大相等的前缀和后缀的数量，与 s[ j ] 无关

next的递推关系

对于模式串的位置 j，有next[ j ] = k，即：p₀p₁…p_k-2p_k-1 = p_j-kp_j-k+1…p_j-2p_j-1
则，对于模式串的位置j+1，考察p[ j ]：
若p[ k ]==p[ j ]（两个黄色部分相等）
next[ j+1 ]=next[ j ]+1

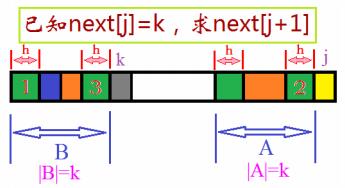
若p[ k ]≠p[ j ]（灰色部分和黄色部分不相等）
记h=next[ k ]，如果p[ h ]==p[ j ]（紫色部分和黄色部分相等），则next[j+1]=h+1，
否则重复此过程。

Python代码

# 计算next数组
def get_next(s):
    size = len(s)
    next = list(range(size))
    next[0] = -1
    k = -1
    j = 0
    # 计算next[j]时，考察的字符串是模式串的前j-1个字符，求其中最大相等的前缀和后缀的数量，与s[j]无关
    while j < size - 1:
        # s[k]表示前缀，s[j]表示后缀
        # k==-1表示未找到k前缀和k后缀相等
        if k == -1 or s[j] == s[k]:
            j += 1
            k += 1
            next[j] = k
        else:
            k = next[k]
    return next


# 计算next数组优化
def get_new_next(s):
    size = len(s)
    next = list(range(size))
    next[0] = -1
    k = -1
    j = 0
    # 计算next[j]时，考察的字符串是模式串的前j-1个字符，求其中最大相等的前缀和后缀的数量，与s[j]无关
    while j < size - 1:
        # s[k]表示前缀，s[j]表示后缀
        # k==-1表示未找到k前缀和k后缀相等
        if k == -1 or s[j] == s[k]:
            j += 1
            k += 1
            if s[j] == s[k]:
                # 特例优化，在和大字符串做匹配的时候
                # 如果s[j]!=大字符串节点的值，则要把s向前滑动到s[k]和大字符串节点做比较
                # 如果s[j] == s[k]，则s[k]也!=大字符串节点的值
                # 这时就需要再次滑动到s[next[k]]做比较
                # 为了减少中间不必要的滑动，直接让s滑动到s[next[k]]就好
                next[j] = next[k]
            else:
                next[j] = k
        else:
            k = next[k]
    return next


# 从文本串ss中找出模式串s第一次出现的位置
def kmp(ss, s):
    ss_len = len(ss)
    s_len = len(s)
    s_next = get_new_next(s)  # 用方法get_next也是可以的，其他代码不变
    i = 0  # ss比较的位置
    j = 0  # s比较的位置
    result = -1  # 结果
    while i < ss_len:
        if j == -1 or ss[i] == s[j]:
            j += 1
            i += 1
        else:
            j = s_next[j]
        if j == s_len:
            result = i - s_len
            break
    return result


if __name__ == '__main__':
    ss = '0123abaabcaba456'
    s = 'abaabcaba'
    next = get_next(s)
    print('计算next数组结果：')
    print(next)
    next = get_new_next(s)
    print('计算next数组优化结果：')
    print(next)
    result = kmp(ss, s)
    print('文本串"%s"第一次出现"%s"的位置:%d' % (ss, s, result))

KMP算法输出结果：

计算next数组结果：
[-1, 0, 0, 1, 1, 2, 0, 1, 2]
计算next数组优化结果：
[-1, 0, -1, 1, 0, 2, -1, 0, -1]
文本串"0123abaabcaba456"第一次出现"abaabcaba"的位置:4

匹配的时间复杂度为O(N)，算上计算next的O(M)时间，整体时间复杂度为O(M+N)

---

暴力求解算法与KMP的区别

假设当前文本串text匹配到 i 位置，模式串pattern串匹配到 j 位置。

暴力求解算法中，如果当前字符匹配成功，即text[i+j]==pattern[j]，令i++，j++，继续匹配下一个字符；
如果失配，即text[i+j]≠pattern[j]，令i++，j=0，即每次匹配失败的情况下，模式串pattern相对于文本串text向右
移动了一位。

KMP算法中，如果当前字符匹配成功，即text[i+j]== pattern[j]，令i++，j++，继续匹配下一个字符；
如果失配，即text[i+j]≠pattern[j]，令 i 不变，j=next[j]，(这里，next[j]≤j-1)，即模式串pattern相对于文本串text向右移动了至少1位(移动的实际位数j-next[j]≥1)

---

KMP应用：PowerString问题

给定一个长度为n的字符串S，如果存在一个字符串T，重复若干次T能够得到S，那么，S叫做周期串，T叫做S的一个周期。
如：字符串abababab是周期串，abab、ab都是它的周期，其中，ab是它的最小周期。
设计一个算法，计算S的最小周期。如果S不存在周期，返回空串

使用next，线性时间解决问题
计算S的next数组；
记k=next[len]，p=len-k；
若len%p==0，则p为最小周期长度，前p个字符就是最小周期。

说明：
使用的是经典KMP的next算法，非变种KMP的next算法；
要“多”计算到len，即next[len]。

思考：如何证明？
考察字符串S的k前缀first和k后缀tail：
1、first和tail的前p个字符
2、first和tail的前2p个字符
3、first和tail的前3p个字符
……

实例分析：如图

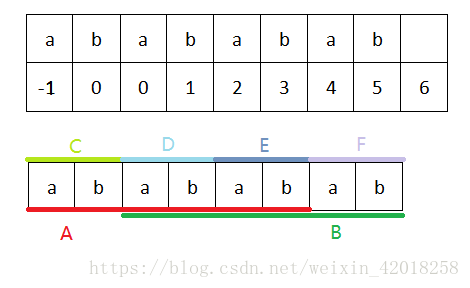
对于字符串s=“abababab”，求出相应的next值，我们多求了一位next[8]=6，说明A=B，其中A=CDE，B=DEF。
len % ( len - next [len] ) = 8 % ( 8 - 6 ) = 0 ， 0说明存在最小周期，最小周期的长度为2（8-6），即为“ab”。
下面就2个字符2个字符的比较：
A的前2个字符C(ab) = B的前2个字符D(ab)
A的前4个字符CD(abab) = B的前4个字符DE(abab)
∵ C=D , CD=DE
∴ CC=CE => C=E => C=D=E
A的前6个字符CDE(ababab)就等于B的前6个字符DEF(ababab)
∵ C=D=E , CDE=DEF
∴ CCC=CCF => C=F => C=D=E=F

Python代码

# 计算next数组
def get_next(s):
    size = len(s)
    next = list(range(size + 1))  # 我们这里要“多”计算到size，即next[size]
    next[0] = -1
    k = -1
    j = 0
    # 计算next[j]时，考察的字符串是模式串的前j-1个字符，求其中最大相等的前缀和后缀的数量，与s[j]无关
    while j < size:  # 要“多”计算到size，即next[size]
        # s[k]表示前缀，s[j]表示后缀
        # k==-1表示未找到k前缀和k后缀相等
        if k == -1 or s[j] == s[k]:
            j += 1
            k += 1
            next[j] = k
        else:
            k = next[k]
    return next


if __name__ == '__main__':
    s = 'abababab'
    next = get_next(s)
    print(next)
    size = len(s)
    if size % (size - next[size]) == 0:
        c = size / (size - next[size])
        print('最小周期：%s' % s[0:size - next[size]])
        print('循环次数：%d' % c)
    else:
        print('没有最小周期')

输出结果：

[-1, 0, 0, 1, 2, 3, 4, 5, 6]
最小周期：ab
循环次数：4

参考七月在线