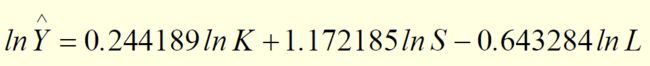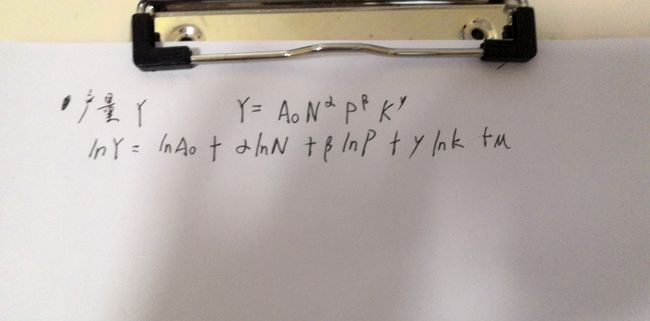数学建模—多元回归分析

EverydayOneCat

木星全貌

知识点

1.笔记

在了接受域中，接受X为0的假设，X对外没有比较显著的线性关系。

2.知识点补充

多元回归模型：含两个以上解释变量的回归模型

多元线性回归模型的假设:

• 解释变量Xi 是确定性变量，不是随机变量
• 解释变量之间互不相关，即无多重共线性
• 随机误差项不存在序列相关关系
• 随机误差项与解释变量之间不相关
• 随机误差项服从0均值、同方差的正态分布

例题

1.多元线性回归

某品种水稻糙米含镉量y(mg/kg)与地上部生物量x1(10g/盆)及土壤含镉量x2(100mg/kg)的8组观测值如表。试建立多元线性回归模型。

1.1SAS代码

data ex;
input x1-x2 y@@;
cards;
1.7 9.08 4.93 12 1.89 1.86
9.67 3.06 2.33 0.76 10.2 5.78
17.67 0.05 0.06 15.91 0.73 0.43
15.74 1.03 0.87 5.41 6.25 3.86
;
proc reg;
model y=x1 x2;
run;

1.2结果分析

我们可以通过WORD将这些复制做成表格更加美观直接，每个表下面都需要有文字说明：

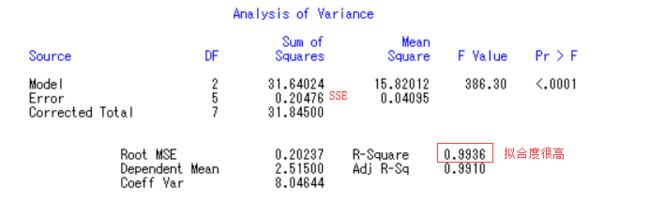
由方差分析表可知，其F value=386.30,pr>F的值<0.0001，远小于0.05，说明F值落在了拒绝域里面，故拒绝原假设，接受备择假设，认为y1与x1,x2之间具有显著性的线性关系；

由参数估计表可知，x2对应的t值为1.61，Pr>|t|的值=0.1691，大于0.05，说明1.61落在了接受域中，接受x2为0的假设，x2对外没有比较显著的线性贡献。

为此，需要在程序中model y1=x1 x2中去掉x2，再次运行：

对常数检验t值分别为t=37.53、,Pr>|t|的值<0.0001,远小于0.05，说明截距项通过检验，估计值为5.67953。
同理可知x1的系数通过检验，估计值为-0.32103

回归方程：y=-0.32103x1+5.67953

许多实际问题中可能还会出现某几个变量的系数并没有通过检验，此时，可以在原程序中的modely1=x1-x2中去掉没用通过的变量,直到所有的系数均通过检验。或者使用逐步回归方法，让软件自动保留通过检验的变量。

2.多元非线性回归

将非线性回归方程转化为线性回归方程。转化时应首先选择适合的非线性回归形式，并将其线性化。再确定线性化回归方程的系
数，最后确定非线性回归方程中未知的系数或参数。

湖北省油菜投入与产出的统计分析

1.投入指标
（1）土地（S）。土地用播种面积来表示。农作物播种面积是指当年从事农业
（2）劳动（L）。劳动用劳动用工数（成年劳动力一人劳动一天为一个工）来表示。劳动用工中包含着直接和间接生产用工。
（3）资本（K）。资本用物质费用来表示。物质费用包含直接费用和间接费用。主要有种子秧苗费、农家肥费、化肥费、农药费、畜力、固定资产折旧费和管理及其他费用等。

2.产出指标
产出指标用湖北省历年油菜生产的总产量(Y)来表示。

2.1SAS代码

data ex;input y k s l t @@;
x1=log(k);x2=log(s);x3=log(l);y1=log(y);
cards;
70.8972 40076.5884 825.1305 15347.4273 1
83.7506 48008.7690 915.1500 15832.0950 2
70.8627 44593.8425 804.150 13306.8090 3
78.3451 43460.3229 783.2100 13314.5700 4
98.0749 72657.2633 923.8050 14596.1190 5
134.8767 146108.3421 1282.8900 20911.1070 7
147.5315 162433.3500 1244.7000 18670.5000 8
154.7607 166979.6325 1330.5150 18627.2100 9
159.9743 190395.5262 1505.4600 20775.3480 10
198.4942 205914.6645 1738.4100 22599.3300 11
194.7943 189762.7335 1677.0900 20963.6250 12
187.1013 193463.610 1761.9450 21936.2153 14
235.1184 183768.4035 1779.1500 19606.2330 15
;
proc reg;model y1=x1 x2 x3 t ; /*selection=stepwise*/
run;

2.2结果分析

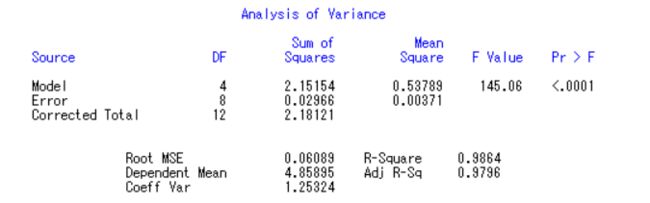
F值为145.06，对应的Pr>F的概率小于0.001，说明F值落在了拒绝域中。故拒绝原假设H0:x1,x2,x3x,t都为0，x1,x2,x3x,t对y1有显著的线性关系。

这里我们遵循一个原则，先看变量，再看常数。变量如果要去，需要一个一个去，因为他们之间可能有线性关系，一个变量会影响另一个变量。

我们可以通过增加一段SAS代码查看变量之间的线性关系。

proc corr;var x1 x2 x3 t;

可以看到，x1 x2 x3 t之间都有线性关系，这种其实是极不稳定的。

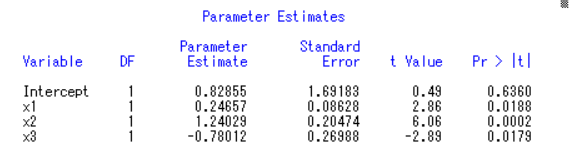
回到上面的表，我们看到常数显著性概率大于0.05，但是我们得先看变量，先不去管他。接着看x3,t都大于0.05很多，我们取最大的t显著性概率为0.9466，远大于0.05。因此将model y1=x1 x2 x3 t;去掉他，即改为model y1=x1 x2 x3 ;

截距项Intercept(常数)的显著性概率为0.6117，大于0.05，因此将model y1=x1 x2 x3 ; 改为model y1=x1 x2 x3/noint;（去掉常数项）

这时候F检验也过了，T检验也过了。我们可以得出式子：

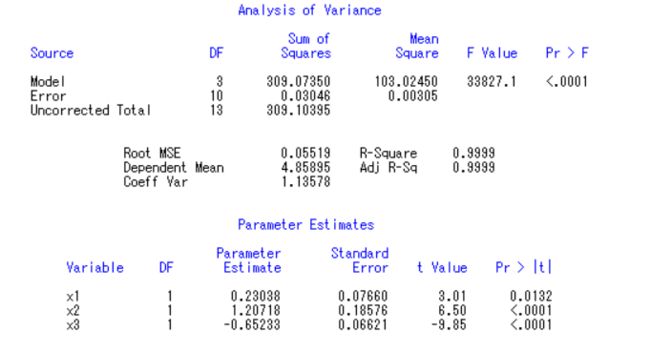
F=34565.8 R2=0.9999 K，S，L的t值分别为（3.01） (6.59) (-9.98)

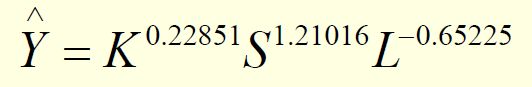
但是我们通过经济学解释就会发现这个式子很不合理：K(资本)增长1%Y增长0.22851%，S(土地)增长1%Y增长1.21%，L(劳动)增长1%Y增长-0.65225%，而且不会随着时间t增长。弹性大于1，这个式子说明湖北省油菜产量主要靠土地来增长，显然不符合现实。本模型虽然满足数学规则，但不能通过经济检验。

上述说明我们刚刚对变量的逐一减法并不适用这一问题，我们可以依据经济学来修改模型：随着现代发展，劳动力其实对产量并无太大影响，反而年数增长带来的技术进步影响更为显著。

model y1=x1 x2 t/noint;

虽然x2依然大于0.05，但是相差并不大，勉强可以算，这样才更符合现实。

3.逐步回归

逐步回归和上面对变量逐一减法想法，他是一个一个把变量加进去，不符合就删掉某个变量。

逐步回归选择变量快捷，但对于存在多重共线的自变量选择，有时并不准确，使用时注意分辨。

SAS使用逐步回归的方法是，模型从y1=x1开始，符合就加成y1=x1 x2，不符合就变成y1=x2…还有一种更为简单的方式，将model y1=x1 x2 x3 t ;
改为model y1=x1 x2 x3 t /selection=stepwise;机器自动判断。

注意，为了筛选变量宽容，程序中默认显著度为0.15，而不是0.05，以避免条件过于严格只用筛选无法进行。

从程序结果中不难看出，x2、x1、t进入模型。因此modely1=x1 x2 x3 t /selection=stepwise;改为model y1=x1 x2 t /noint;再运行一遍即可。

4.标准化回归

由于单位量纲不一样，偏回归系数的大小不能完全反映自变量对因变量影响的大小。要想真实反映自变量的贡献，标准化回归是个好的选择。

标准化回归系数（Beta值）在多元回归中被用来比较变量间的重要性。

还是用上面的例子，将model y1=x1 x2 t /noint;改为model y1=x1 x2 t /noint stb;运行即可。

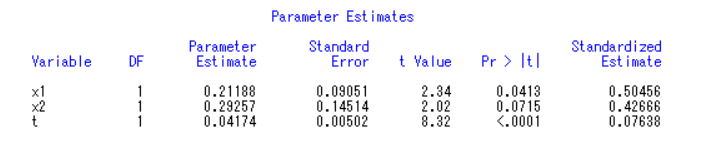
从最后一列（标准化回归系数）可看出，x1重要性超过x2和t。与原先的参数大小比有变化。

同时这个也符合现实，在现实生活中，湖北省油菜很大的产量来自于资本的投资。

作业

1.问题一的分析与求解

为探究各种化肥（主要为N 、P 、K 肥）的投入量对于土豆产量的影响程度大小，我们决定使用多元回归模型，通过比较回归方程系数的大小来比较各种化肥的投入量对土豆产量影响程度的大小。

编写SAS代码：

data ex;input n p k y@@;
x1=log(n);x2=log(p);x3=log(k);y1=log(y);
cards;
0 196 372 15.18
34 196 372 21.36
67 196 372 25.72
101 196 372 32.29
435 196 372 34.03
202 196 372 39.45
259 196 372 43.15
336 196 372 43.46
404 196 372 40.83
471 196 372 30.75
259 0 372 33.46
259 24 372 32.47
259 49 372 36.06
259 73 372 37.96
259 98 372 41.04
259 147 372 40.09
259 196 372 41.26
259 245 372 42.17
259 294 372 40.36
259 342 372 42.73
259 196 0 18.98
259 196 47 27.35
259 196 93 34.86
259 196 140 38.52
259 196 186 38.44
259 196 279 37.73
259 196 372 38.43
259 196 465 43.87
259 196 558 42.77
259 196 651 46.22
;
proc reg;model y1=x1 x2 x3;
proc corr;var x1 x2 x3;
run;

首先我们对自变量x1、x2、x3 之间的相关性进行判断，计算得相关系数如下表：

通过相关系数表我们可以看出各自变量之间得相关系数的绝对值均小于0.09，因此可以认为自变量之间无相关性，使用多元回归分析效果较好。

接着使用最小二乘法对自变量和因变量进行多元回归分析，对得到的回归方程进行F检验，得到方差分析表：

由方差分析表可知，其 F value=11.95，对应的Pr>F的概率小于0.001，故11.95落在了拒绝域中，拒绝原假设H0：x1,x2,x3都为0。认为y1 与x1、x2、x3 之间有显著性的线性关系。

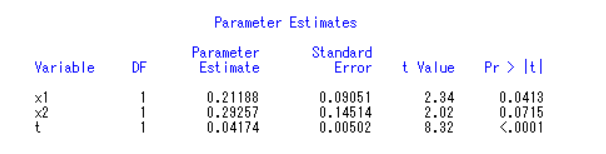
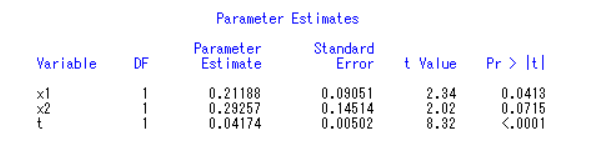
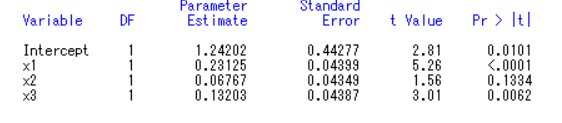
接着对各参数进行显著性检验，通过t 检验得到如下参数估计表：

由参数估计表可知：

（1）对自变量x1检验的t值为5.26，Pr>|t|的值小于0.001，因此拒绝原假设认为x1系数为0，说明x1的系数通过检验，x1与y1有显著的线性关系。

（2）对自变量x2 检验的t 值为t=1.56，Pr>|t|的值=0.1334，大于0.05，因此接受原假设认为x2 系数为0，说明x2 的系数没有通过检验，x2 与y 没有显著的线性关系，且其回归系数最小，即x2 对y 的影响不明显，因此在回归方程中去除自变量x2。

（3）对自变量x3 检验的t 值为t=3.01，Pr>|t|的值=0.0062，小于0.05，因此拒绝原假设认为x3 系数为0，说明x3 的系数通过检验，x1 与y 有显著的线性关系。

去除变量x2 后，继续对y 与x1、x3 进行回归分析，步骤同上。在方程通过F 检验后得到如下参数估计表：

但是我们考虑到现实生活，磷肥不可能毫无影响，这里我们注意，下面的题目是让我们预测，当我们做预测这种题型时，其实T检验没有那么严格，我们只需要保证F检验拒绝原假设就可以了。我们可以保留x2，增加一句话：x2对结果没有线性影响。

x1>x3>x2，综上所述，化肥种类对土豆产量影响程度由大到小的排列顺序为氮肥、钾肥和磷肥。

2.问题二的分析与求解

经验之谈：一般这种求因变量极值的问题建模都用二次函数

编写SAS代码：

data ex;input n p k y@@;
x1=n*n;x2=p*p;x3=k*k;x4=n*p;x5=n*k;x6=p*k;
cards;
/*同上数据区*/
;
proc reg;model y=n p k x1-x6;
run;

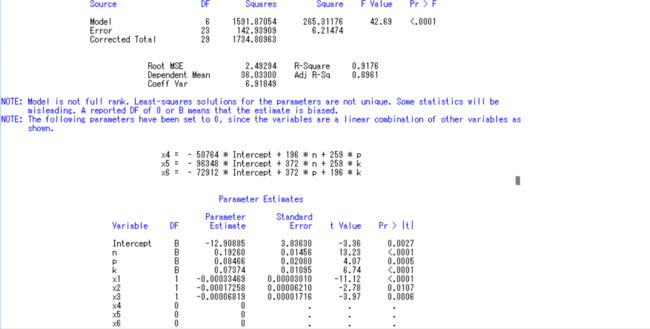
运行结果：

我们发现运行后SAS警告我们x4,x5,x6和我们的n,p,k有线性关系，高度共线，也就是说，我们通过n,p,k完全可以表示x4,x5,x6：
$$x4=-50764\ast Intercept+196\ast n+259\ast p$$

$$x5=-96348\ast Intercept+372\ast n+259\ast k$$

$$x6=-72912\ast Intercept+372\ast p+196\ast k$$

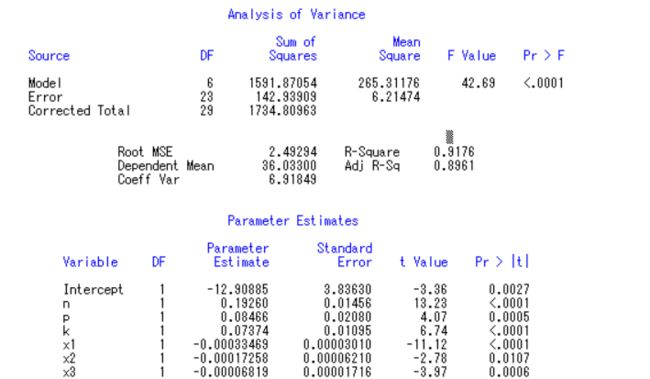
因此，需要去掉x4,x5,x6：model y=n p k x1-x3;再次运行，结果如下：

我们发现无论是F检验还是T检验都很完美，符合度也高达91.76%，我们可以根据此写出我们的式子：
$$y=-12.91+0.1926\ast n+0.0847\ast p+0.074\ast k-0.00033469\ast x1-0.00017258\ast x2-0.00006819\ast x3$$
统计学检验通过了，我们需要来检验模型拟合精度，看误差率是多少。

SAS代码：

data ex;input n p k y@@;
x1=n*n;x2=p*p;x3=k*k;x4=n*p;x5=n*k;x6=p*k;
y1=-12.91+0.1926*n+0.0847*p+0.074*k-0.00033469*x1-0.00017258*x2-0.00006819*x3;
red=y-y1;wucha=abs(y-y1)/y*100;wc+wucha;
cards;
/*同上数据区*/
;
proc print;var y y1 red wucha wc;
run;

我们发现平均误差率是147.322/30=4.9%左右，说明我们求得这个式子还算可以。接下来我们要Y最大，只需要对这三个变量求偏导即可求出，这里我们可以用LinGO软件。

max=y;
y=-12.91+0.1926*n+0.0847*p+0.074*k-0.00033469*n*n-0.00017258*p*p-0.00006819*k*k;
n*p=- 50764 * Intercept + 196 * n + 259 * p;
n*k=- 96348 * Intercept + 372 * n + 259 * k;
p*k=- 72912 * Intercept + 372 * p + 196 * k;

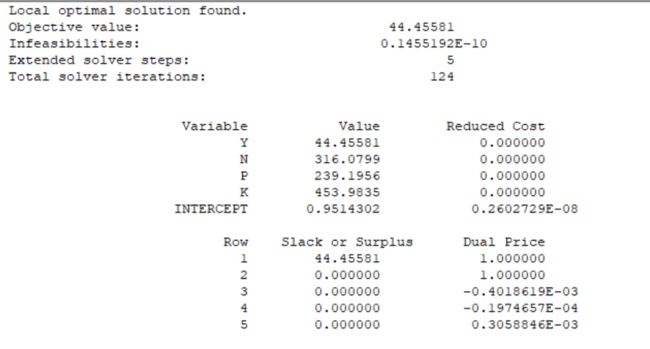
执行结果：

可以看出，当氮肥316.0799kg，磷肥239.1956kg，钾肥453.9835kg时产量最高。

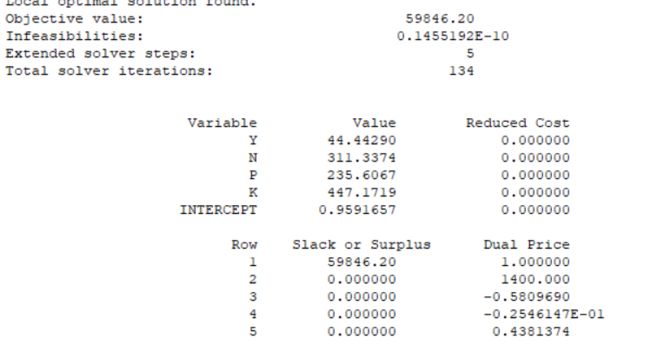
3.问题三的分析与求解

max=1.4*1000*y-2.8*n-2.2*p-2.2*k;
y=-12.91+0.1926*n+0.0847*p+0.074*k-0.00033469*n*n-0.00017258*p*p-0.00006819*k*k;
n*p=- 50764 * Intercept + 196 * n + 259 * p;
n*k=- 96348 * Intercept + 372 * n + 259 * k;
p*k=- 72912 * Intercept + 372 * p + 196 * k;

结语

高考的xdm加油！分享一首我高中高考冲刺的歌(●ˇ∀ˇ●)