模拟退火算法解决TSP问题
转载自:http://cighao.com/2015/12/04/solve-TSP-with-SA/
https://blog.csdn.net/on2way/article/details/40216517
1. 什么是 TSP 问题
旅行商问题,即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
2. 什么是模拟退火算法
关于模拟退火算法请参考之前发的一篇文章,模拟退火详解
3. 求解思想
关于解的形式,肯定是一组点的序列,表示了访问顺序。第一个点和最后一个点相同,均为起点。
假设所有的点分别为 {v1,v2,…,vn},起点为 v1。
(1)解空间
解空间 S 可表为的所有固定起点和终点的循环排列集合,即
S={(π1,π2…,πn,π1)|π1=v1,(π2,…,πn)为{v2,v3,…,vn}的一个排列}。
S 中的每一个排列表示一个回路,也就是一个解。 πi=j 表示在第 i-1 次访问目标 j。
(2)目标函数
此时的目标函数为访问所有目标的路径长度或称代价函数。我们要求
minf(π1,π2…,πn,π1)=∑1nd
(3)新解的产生
任选序号 u,v(u < v)交换u与v之间的顺序产生新的路径
4.我要解决的问题
既然SA是优化算法,那就用它来解决旅行商问题,也叫TSP问题。问题是什么样子的呢,就是随机给你不同的地点,要你每个地点走一次的话,怎么走这个地点的顺序才能使得你走的总路程最短呢,像这类问题最好的验证实例就是邮递员了吧,他会想怎么邮递所有的包裹才能使得他要走的总路线最少吧。好了下面我随便给出30个不同的点代表不同的位置吧,点的左边都在0~1之间,如下:
cities1=[0.6606,0.9695,0.5906,0.2124,0.0398,0.1367,0.9536,0.6091,0.8767,0.8148,0.3876,0.7041,0.0213,0.3429,0.7471,0.4606,0.7695,0.5006,0.3124,0.0098,0.3637,0.5336,0.2091,0.4767,0.4148,0.5876,0.6041,0.3213,0.6429,0.7471;
0.9500,0.6740,0.5029,0.8274,0.9697,0.5979,0.2184,0.7148,0.2395,0.2867,0.8200,0.3296,0.1649,0.3025,0.8192,0.6500,0.7420,0.0229,0.7274,0.4697,0.0979,0.2684,0.7948,0.4395,0.8867,0.3200,0.5296,0.3649,0.7025,0.9192];
注意了,这就是30对(x,y)的值,在matlab下画出来就如图所示:
plot(cities1(1,:),cities1(2,:),’*’)
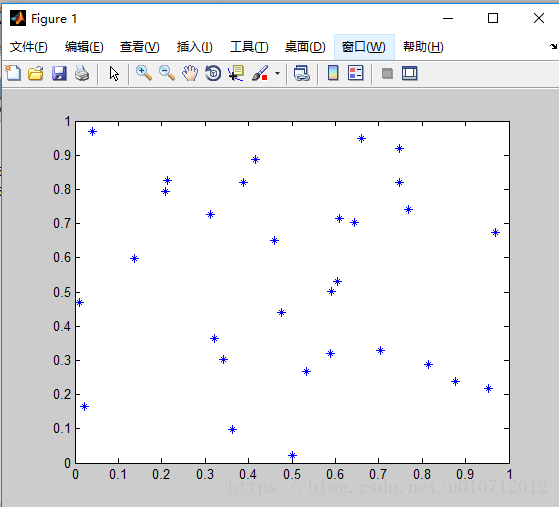
现在问题就是怎么首尾相连这些点才能是他们点之间的距离最小。
5.如何开展算法
地点知道了那么剩下的就是如何开始了。首先最关键的就是点的顺序问题。上面我们给了一系列点,我们的假设就是那些点的先后顺序就是我们要走的顺序,而算法的开展就是改变那些点的循序。比如说上面的点中,第一个点是(0.6606,0.6606),第五个点是(0.0398,0.0398)吧,其他的类似就不说了,那么开始走的顺序就是从第一个点走到第二个点,然后再到第三个点,等等。好了,那么如果我把第一、五的位置换一下,现在第一个要走的点是(0.0398,0.0398),第五个要走的点就是(0.0398,0.0398),其他都先不变的话,那么你想想没变化前你从一点走到二点的距离和变化后你从一点走到二点的距离一样吗?显然不一样。那么好了,不一样就会有大小吧,记录所有距离和的较小者,ok了。并且这种交换可不是只有两个两个交换呀,可以多个相互交换。并且可以交换多次,这样可以产生多少组不同的走法呀,里面不乏有更好的解吧。讲到这里我们也就清楚了我们有哪些事情要干了吧,首先,得有一个负责交换点的函数吧,换完后,肯定还的有一个针对这种顺序下求他们的相互顺序点点之间所有距离和的函数吧。还有一个就是模拟退火的精髓函数,它是决定着某次交换操作后根据所得的结果来决定是否接受本次交换的函数。参考模拟退火详解
%-------------函数说明----------------
% 交换地点顺序
% 输入变量:
% inputcities:原来的地点顺序和位置
% n: 要交换的次数(即多少对地点相交换)
% 输出变量:
% s:交换后的地点顺序和位置
%---------------------------------------
function s = swapcities(inputcities,n)
s = inputcities;
for i = 1 : n
city_1 = round(length(inputcities)*rand(1));%生成随机交换点(1~30之间
%吧)round 四舍五入
if city_1 < 1 %小于1取1,最小不也就是1吗
city_1 = 1;
end
city_2 = round(length(inputcities)*rand(1));
if city_2 < 1
city_2 = 1;
end
temp = s(:,city_1); %交换操作,c语言中不经常这么替换吗
s(:,city_1) = s(:,city_2);
s(:,city_2) = temp;
end
%-------------函数说明----------------
% 距离计算函数
% 输入变量:
% inputcities:原来的地点顺序和位置
% 输出变量:
% d:顺序相加的距离和
%---------------------------------------
function d = distance(inputcities) %城市距离求和
d=0;
for n = 1:length(inputcities)
if n == length(inputcities) %首尾的距离计算
d = d + norm(inputcities(:,n) - inputcities(:,1));
else
d = d + norm(inputcities(:,n) - inputcities(:,n+1)); %相邻两个点的距离
end
end
对其中norm解释一下,norm是一个求范数的操作,范数某种意义上就是长度、大小、距离的意思,在这里看看,norm里面是不是x和y的坐标差呀,这样算后就是这两个点之间的距离,不明白的就可以认为是对坐标差的(x2+y2)开方,勾股定理明白吧,就是它了,比如norm(3,4)=norm(4,3)=norm(-3,4)=norm(-4,-3),是多少,都是5,这就是范数。
%-------------函数说明----------------
% 模拟退火函数
% 输入变量:
% inputcities:原来的地点顺序和位置
% initial_temperature:初始温度
% cooling_rate: 降温比例系数
% threshold : 一个循环次数
% numberofcitiestoswap : 每次交换地点的对数
%---------------------------------------
function simulatedannealing(inputcities,initial_temperature,cooling_rate,threshold,numberofcitiestoswap) %退火算法
tempeature = initial_temperature; %初始温度
input_cities = inputcities; %城市坐标
plot(input_cities(1,:),input_cities(2,:),'*');
%画出开始图像,与后面对比
hold on,plot(input_cities(1,:),input_cities(2,:));
figure;
while tempeature > 0.01 %循环条件,把降温底线作为条件
for i = 1 : threshold %循环次数
previous_distance = distance(input_cities); %旧距离和
temp_cities = swapcities(input_cities,numberofcitiestoswap);
%随机n次交换
current_distance = distance(temp_cities); %新距离和
diff = abs(current_distance - previous_distance); %产生误差
if current_distance < previous_distance
%距离变少了,直接接受,不用考虑
input_cities = temp_cities; %接受
else if rand(1) < exp(-diff/(tempeature)) %否则,以一定的概率接受
input_cities = temp_cities; %概率符合了,进来接受
end
end
end
tempeature = tempeature*cooling_rate; %降温过程
end
fprintf('\t\t\tTempeature = %3.8f\n',tempeature); %输出结果
current_distance = distance(input_cities);
fprintf('\t\t\tFinal_istance = % 3.8f\n',current_distance);
plot(input_cities(1,:),input_cities(2,:),'*');
hold on,plot(input_cities(1,:),input_cities(2,:));
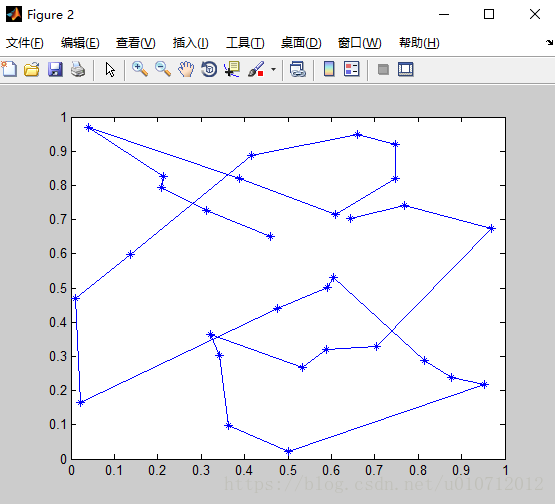
Tempeature = 0.00993111
Final_istance = 5.29570947
这是我的某次运行出来的结果图,可以看到总的行走距离为5.29570947,当然这是我运行了好多回,并且不断调整simulatedannealing里面的参数来的比较好的一个结果,每次的结果还都不一样,大致都在5~8之间,并且我感觉这肯定不是最优解,最优解应该比这个还小才对。不过这是最基础的算法了,没有一点改进,比如说降温率固定了,循环次数固定了,每次交换对数固定了等等,能达到这个效果还行吧。如果再好好对这个算法进行改善下,比如说把这些固定的值改为动态改变的话,效果肯定会好些,具体怎么改善算法,可以去看相关专业文献,明白了模拟退火的基本原理再去改善就很好理解了。