Matlab模拟退火算法解决TSP问题
Matlab模拟退火算法解决TSP问题
- 问题描述
- 求解思路
- 1. 读取数据
- 2. 求解距离矩阵
- 3. 用蒙特卡洛方法产生一个初始解
- 4. 模拟退火过程
- (1) 解空间
- (2) 目标函数
- (3) 新解的产生
- (4) 代价函数差
- (5) 接受准则
- (6) 降温
- (7) 结束条件
- 5. 数据可视化
- 全部代码
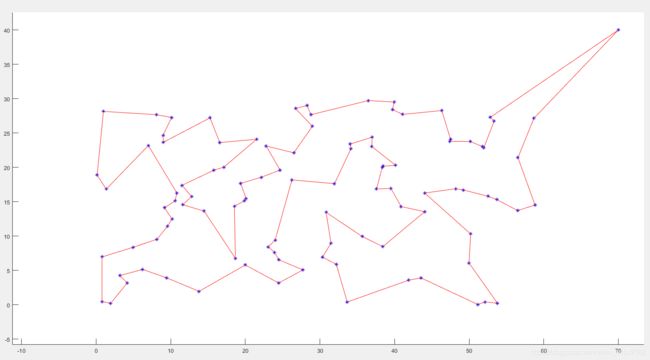
- 结果
- 附录
问题描述
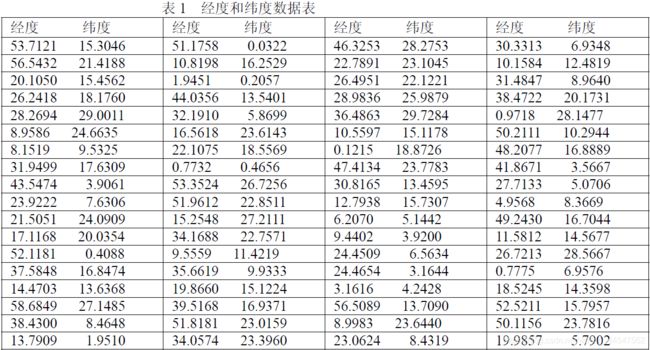
已知敌方100 个目标的经度、纬度如表1 所示。

在地图上显示如下:
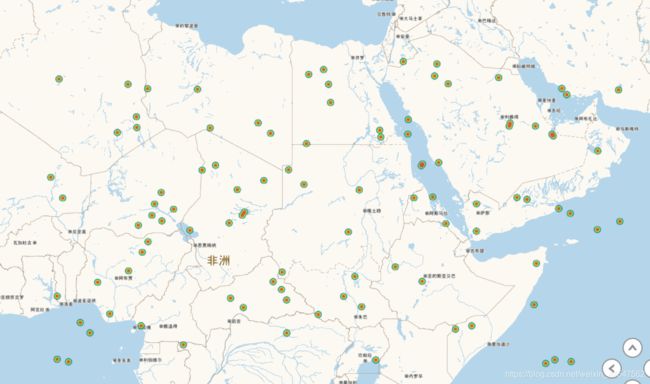
我方有一个基地,经度和纬度为(70,40)。假设我方飞机的速度为1000 公里/小时。我方派一架飞机从基地出发,侦察完敌方所有目标,再返回原来的基地。在敌方每一目标点的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
求解思路
这是一个旅行商问题。我们依次给基地编号为1,敌方目标依次编号为2,3,…,101,最后我方基地再重复编号为 102(这样便于程序中计算)。距离矩阵 D = ( d i j ) 102 × 102 D=(d_{ij})_{102\times102} D=(dij)102×102,其中 d i j d_{ij} dij 表示表示 i , j i,j i,j 两点的距离, i , j = 1 , 2 , … , 102 i, j = 1,2, \dotso,102 i,j=1,2,…,102,这里 D D D为实对称矩阵。则问题是求一个从点1 出发,走遍所有中间点,到达点102 的一个最短路径。
1. 读取数据
先把xlsx文件中的数据保存在变量 data1 中,把基地设为home,则最终的数据为data = [home; data1; home]。将data再保存到data_plot变量中,方便后面的画图操作。
代码如下:
% 初始化各种参数
T = 1000; % 设置初始温度
derate = 0.99; % 设置退火率
T_min = 1e-10; % 设置最小温度
L = 0; % 迭代次数
data1 = xlsread('飞行点坐标.xlsx'); % 读取数据
home = [70, 40];
data = [home;data1;home];
data_plot = [home;data1;home];
2. 求解距离矩阵
因为文件中给的数据是需侦察点的经纬度,所以需要求实际距离。设A, B两点的地理坐标分别为(x1, y1), (x2, y2),过 A, B两点的大圆的劣弧长即为两点的实际距离。以地心为坐标原点O,以赤道平面为XOY 平面,以0 度经线圈所在的平面为 XOZ 平面建立三维直角坐标系。则 A, B两点的直角坐标分别为:
A ( R cos x 1 cos y 1 , R sin x 1 cos y 1 , R sin y 1 ) A(R \cos x_1 \cos y_1, R \sin x_1 \cos y_1, R \sin y_1) A(Rcosx1cosy1,Rsinx1cosy1,Rsiny1)
A ( R cos x 2 cos y 2 , R sin x 2 cos y 2 , R sin y 2 ) A(R \cos x_2 \cos y_2, R \sin x_2 \cos y_2, R \sin y_2) A(Rcosx2cosy2,Rsinx2cosy2,Rsiny2)
其中 R = 6370为地球半径。
A, B两点的实际距离
d = R arccos ( O A → ⋅ O B → ∣ O A → ∣ ⋅ ∣ O B → ∣ ) d = R \arccos{\biggl(\dfrac{\overrightarrow{OA}\cdot\overrightarrow{OB}}{\lvert\overrightarrow{OA}\lvert\cdot\lvert\overrightarrow{OB}\lvert}\biggl)} d=Rarccos(∣OA∣⋅∣OB∣OA⋅OB)
化简得
d = R arccos [ cos ( x 1 − x 2 ) cos y 1 cos y 2 + sin y 1 s i n y 2 ] d=R\arccos{\mathbf{[}\cos{(x_1-x_2)}\cos{y_1}\cos{y_2}+\sin{y_1}sin{y_2}\mathbf{]}} d=Rarccos[cos(x1−x2)cosy1cosy2+siny1siny2]
代码如下:
data = data * pi / 180;
R = 6370; % 地球半径
% 求解距离矩阵
for i = 1:length(data)
for j = 1:length(data)
D(i,j) = R*acos(cos(data(i,1)-data(j,1))*cos(data(i,2))*cos(data(j,2))+sin(data(i,2))*sin(data(j,2)));
end
end
3. 用蒙特卡洛方法产生一个初始解
解空间S 可表为 { 1 , 2 , … , 101 , 102 } \{1,2, \dotso,101,102 \} {1,2,…,101,102}的所有固定起点和终点的循环排列集合,即
S = { ( π 1 , π 2 , … , π 102 ) ∣ π 1 = 1 , ( π 2 , … , π 101 ) 为 { 2 , 3 , … , 101 } 的 循 环 排 列 , π 102 = 102 ) S=\{(\pi_1,\pi_2,\dotso,\pi_{102})|\pi_1=1,(\pi_2,\dotso,\pi_{101})为\{2,3,\dotso,101\}的循环排列,\pi_{102}=102) S={(π1,π2,…,π102)∣π1=1,(π2,…,π101)为{2,3,…,101}的循环排列,π102=102)
循环1000次或更多次,每次循环随机产生解空间,以1开头,以102结尾。每次循环都和上次的总距离Sum比较,如果比上次的总距离小,则此次循环产生的解空间更好。
代码如下:
% 用蒙特卡洛方法产生一个较好的初始解
Sum = inf; % 初始化总路径长度为无穷大
for i = 1:1000
S=[1,1+randperm(100),102]; % 随机产生解空间S,以1为开头,102为结尾
temp = 0;
for j=1:101
temp=D(S(j),S(j+1));
end
if temp < Sum
S0 = S;
Sum = temp;
end
end
4. 模拟退火过程
求解的模拟退火算法描述如下:
(1) 解空间
解空间S 可表为{1,2, … \dotso …,101,102 }的所有固定起点和终点的循环排列集合,即
S = { ( π 1 , π 2 , … , π 102 ) ∣ π 1 = 1 , ( π 2 , … , π 101 为 { 2 , 3 , … , 101 } 的 循 环 排 列 , π 102 = 102 ) S=\{(\pi_1,\pi_2,\dotso,\pi_{102})|\pi_1=1,(\pi_2,\dotso,\pi_{101}为\{2,3,\dotso,101\}的循环排列,\pi_{102}=102) S={(π1,π2,…,π102)∣π1=1,(π2,…,π101为{2,3,…,101}的循环排列,π102=102)
其中每一个循环排列表示侦察 100 个目标的一个回路, π i = j \pi_i=j πi=j 表示在第 i i i次侦察 j j j点,初始解可选为(1,2, … \dotso …,102),本文中我们使用 Monte Carlo 方法求得一个较好的初始解。
(2) 目标函数
此时的目标函数为侦察所有目标的路径长度或称代价函数。我们要求
min f ( π 1 , π 2 , … π 102 ) = ∑ i = 1 101 d π i π i + 1 \min f(\pi_1,\pi_2,\dotso\pi_{102})=\displaystyle\sum_{i=1}^{101}d_{\pi_i\pi_{i+1}} minf(π1,π2,…π102)=i=1∑101dπiπi+1
而一次迭代由下列三步构成:
(3) 新解的产生
2 变换法
任选序号 u , v u,v u,v ( u < v ) (u
π 1 … π u − 1 π v π v + 1 … π u + 1 π u π v + 1 … π 102 \pi_1\dotso\pi_{u-1}\pi_v\pi_{v+1}\dotso\pi_{u+1}\pi_u\pi_{v+1}\dotso\pi_{102} π1…πu−1πvπv+1…πu+1πuπv+1…π102
(4) 代价函数差
对于2 变换法,路径差可表示为
Δ f = ( d π u − 1 π v + d π u π v + 1 ) − ( d π u − 1 π u + d π v π v + 1 ) \Delta f=(d_{\pi_{u-1}\pi_v}+d_{\pi_u\pi_{v+1}})-(d_{\pi_{u-1}\pi_u}+d_{\pi_v\pi_{v+1}}) Δf=(dπu−1πv+dπuπv+1)−(dπu−1πu+dπvπv+1)
(5) 接受准则
P = { 1 Δ f < 0 exp ( − Δ f / T ) Δ f ≥ 0 P=\begin{dcases} 1 &\Delta f<0 \\ \exp(-\Delta f/T) &\Delta f\ge0 \end{dcases} P={1exp(−Δf/T)Δf<0Δf≥0
如果 Δ f < 0 \Delta f<0 Δf<0,则接受新的路径。否则,以概率 exp ( − Δ f / T ) \exp(-\Delta f/T) exp(−Δf/T)接受新的路径,即若 exp ( − Δ f / T ) \exp(-\Delta f/T) exp(−Δf/T)大于 0 到1之间的随机数则接受。
(6) 降温
利用选定的降温系数 α \alpha α进行降温即: T ← α T T\leftarrow\alpha T T←αT,得到新的温度,这里我们取 α = 0.999 \alpha=0.999 α=0.999。
(7) 结束条件
用选定的终止温度 T _ m i n = 1 0 − 10 T\_min=10^{-10} T_min=10−10,判断退火过程是否结束。若 T < T _ m i n T
当前状态。
代码如下:
% 模拟退火
hold on
while T > T_min
% 2变换法产生新解
change = 1+ceil(100*rand(1,2));
change = sort(change);
u = change(1);
v = change(2);
% 求与上一个解的差
delta_Sum = D(S0(u-1),S0(v))+D(S0(u),S0(v+1))-D(S0(u-1),S0(u))-D(S0(v),S0(v+1));
% 接受准则
if delta_Sum < 0
S0=[S0(1:u-1),S0(v:-1:u),S0(v+1:102)];
Sum = 0;
for j=1:101
Sum=Sum + D(S0(j),S0(j+1));
end
elseif exp(-delta_Sum/T)>rand(1)
S0=[S0(1:u-1),S0(v:-1:u),S0(v+1:102)];
Sum = 0;
for j=1:101
Sum=Sum + D(S(j),S(j+1));
end
end
L = L+1;
% 画迭代图
if mod(L, 50)==0
scatter(L, Sum,'.b');
end
T = T*derate;
end
xlabel("迭代次数");
ylabel("总路程");
hold off
5. 数据可视化
%可视化
figure
hold on
%画点
for i = 1:102
scatter(data_plot(S0(i),1),data_plot(S0(i),2),'*b')
end
%画线
for i = 1:101
plot([data_plot(S0(i),1),data_plot(S0(i+1),1)], [data_plot(S0(i),2),data_plot(S0(i+1),2)],'r')
end
title("路线图");
hold off
Time = Sum/1000;
fprintf('总路程为%.4f km\n花费时间为%.4f h\n',Sum,Time);
全部代码
clear;
clc;
data1 = xlsread('飞行点坐标.xlsx'); % 读取数据
home = [70, 40];
data = [home;data1;home];
data_plot = [home;data1;home];
data = data * pi / 180;
R = 6370; % 地球半径
% 求解距离矩阵
for i = 1:length(data)
for j = 1:length(data)
D(i,j) = R*acos(cos(data(i,1)-data(j,1))*cos(data(i,2))*cos(data(j,2))+sin(data(i,2))*sin(data(j,2)));
end
end
% 初始化各种参数
T = 1000; % 设置初始温度
derate = 0.99; % 设置退火率
T_min = 1e-100; % 设置最小温度
L = 0; % 迭代次数
% 用蒙特卡洛方法产生一个较好的初始解
Sum = inf; % 初始化总路径长度为无穷大
for i = 1:1000
S=[1,1+randperm(100),102]; % 随机产生解空间S,以1为开头,102为结尾
temp = 0;
for j=1:101
temp=D(S(j),S(j+1));
end
if temp < Sum
S0 = S;
Sum = temp;
end
end
% 模拟退火
hold on
while T > T_min
% 2变换法产生新解
change = 1+ceil(100*rand(1,2));
change = sort(change);
u = change(1);
v = change(2);
% 求与上一个解的差
delta_Sum = D(S0(u-1),S0(v))+D(S0(u),S0(v+1))-D(S0(u-1),S0(u))-D(S0(v),S0(v+1));
% 接受准则
if delta_Sum < 0
S0=[S0(1:u-1),S0(v:-1:u),S0(v+1:102)];
%S0 = [S0(1:u-1), v, S0(u+1:v-1), u, S0(v+1:length(data))];
Sum = 0;
for j=1:101
Sum=Sum + D(S0(j),S0(j+1));
end
elseif exp(-delta_Sum/T)>rand(1)*5
S0=[S0(1:u-1),S0(v:-1:u),S0(v+1:102)];
Sum = 0;
for j=1:101
Sum=Sum + D(S0(j),S0(j+1));
end
end
L = L+1;
% 画迭代图
if mod(L, 50)==0
scatter(L, Sum,'.b');
end
T = T*derate;
end
xlabel("迭代次数");
ylabel("总路程");
hold off
% 可视化
figure
hold on
% 画点
for i = 1:102
scatter(data_plot(S0(i),1),data_plot(S0(i),2),'*b')
end
% 画线
for i = 1:101
plot([data_plot(S0(i),1),data_plot(S0(i+1),1)], [data_plot(S0(i),2),data_plot(S0(i+1),2)],'r')
end
title("路线图");
hold off
Time = Sum/1000;
fprintf('总路程为%.4f km\n花费时间为%.4f h\n',Sum,Time);