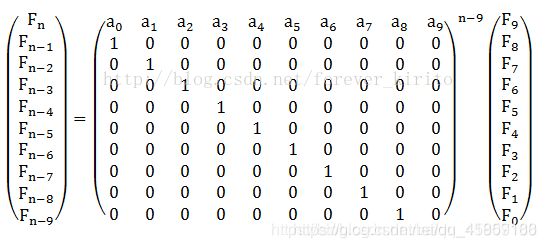
矩阵快速幂入门
Powered by:AB_IN 局外人
NEFU459 A Simple Math Problem
更新后的写法
#include NEFU461 fibs的位数
广义斐波那契数列。
a n = u ∗ a n − 1 + v ∗ a n − 2 an=u*a_{n−1}+v*a_{n−2} an=u∗an−1+v∗an−2
a 0 = a , a 1 = b a_0=a,a_1=b a0=a,a1=b
x = u + u 2 + 4 v 2 , y = u − u 2 + 4 v 2 x=\frac {u+\sqrt{u^2+4v}}2,y=\frac {u-\sqrt{u^2+4v}}2 x=2u+u2+4v,y=2u−u2+4v
则 a n = ( b − a y ) x n x − y a_n=\frac {(b−ay)x^n} {x−y} an=x−y(b−ay)xn
对 a n a_n an取对数加一即可:
l e n = n l o g 10 ( x ) + l o g 10 ( b − a y ) − l o g 10 ( x − y ) + 1 len=nlog_{10}(x)+log_{10}(b−ay)−log_{10}(x−y)+1 len=nlog10(x)+log10(b−ay)−log10(x−y)+1
#include NEFU462 fibs的组合
一开始看这题一点思路都没有,那就先打表!
#include 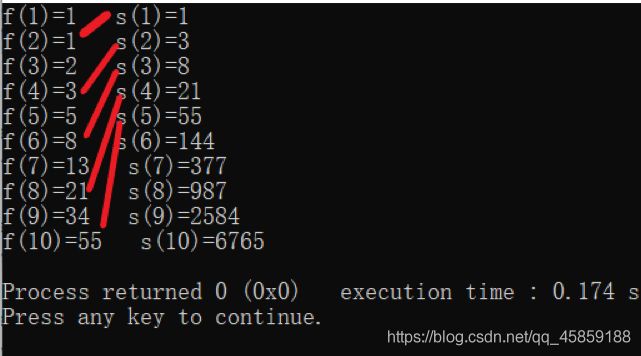
观察到 S ( n ) = f ( 2 n ) S(n)=f(2n) S(n)=f(2n)
那就好做多了!找循环节即可!
#include #include NEFU463 Fibs之和
可以推出规律为:
S ( n ) = f ( n + 2 ) − f ( 2 ) S(n)=f(n+2)-f(2) S(n)=f(n+2)−f(2)
所以求 a a a到 b b b的和,就是
S ( b ) − S ( a − 1 ) = f ( b + 2 ) − f ( a + 1 ) S(b)-S(a-1) \\ =f(b+2)-f(a+1) S(b)−S(a−1)=f(b+2)−f(a+1)
代码孕育而生。
#include NEFU457 Not Fibonacci
如果结果是负数可以这么处理(ans+mod)%mod.
f ( n ) = p ∗ f ( n − 1 ) + q ∗ f ( n − 2 ) f(n) = p*f(n - 1) + q*f(n - 2) f(n)=p∗f(n−1)+q∗f(n−2)
f ( 0 ) = a , f ( 1 ) = b f(0) = a, f(1) = b f(0)=a,f(1)=b
记录一下怎么求出来的 n − 1 n-1 n−1
{ 1 p q 0 p q 0 1 0 } 1 ∗ { s ( 1 ) f ( 1 ) f ( 0 ) } = { s ( 2 ) f ( 2 ) f ( 1 ) } \left\{ \begin{matrix} 1 & p & q \\ 0 & p & q \\ 0 & 1 & 0 \end{matrix} \right\}^1 *\left\{ \begin{matrix} s(1) \\ f(1) \\ f(0) \end{matrix} \right\} =\left\{ \begin{matrix} s(2) \\ f(2) \\ f(1) \end{matrix} \right\} ⎩⎨⎧100pp1qq0⎭⎬⎫1∗⎩⎨⎧s(1)f(1)f(0)⎭⎬⎫=⎩⎨⎧s(2)f(2)f(1)⎭⎬⎫
- 首先就是推出上面的这个式子,等号左边只有一列的这个矩阵,一定要出现最小的值,比如 f ( 0 ) f(0) f(0)。
- 然后,推出来的矩阵的1次方,就对应一下等号右边的1,比如 f ( 1 ) f(1) f(1)。
- 然后就可以推出下面的式子了!
{ 1 p q 0 p q 0 1 0 } n ∗ { s ( 1 ) f ( 1 ) f ( 0 ) } = { s ( n + 1 ) f ( n + 1 ) f ( n ) } \left\{ \begin{matrix} 1 & p & q \\ 0 & p & q \\ 0 & 1 & 0 \end{matrix} \right\} ^{n}*\left\{ \begin{matrix} s(1) \\ f(1) \\ f(0) \end{matrix} \right\} =\left\{ \begin{matrix} s(n+1) \\ f(n+1) \\ f(n) \end{matrix} \right\} ⎩⎨⎧100pp1qq0⎭⎬⎫n∗⎩⎨⎧s(1)f(1)f(0)⎭⎬⎫=⎩⎨⎧s(n+1)f(n+1)f(n)⎭⎬⎫
要求的是 s ( n ) s(n) s(n),把 n n n转换成 n − 1 n-1 n−1就行了。
{ 1 p q 0 p q 0 1 0 } n − 1 ∗ { a + b b a } = { s ( n ) f ( n ) f ( n − 1 ) } \left\{ \begin{matrix} 1 & p & q \\ 0 & p & q \\ 0 & 1 & 0 \end{matrix} \right\} ^{n-1}*\left\{ \begin{matrix} a+b \\ b \\ a \end{matrix} \right\} =\left\{ \begin{matrix} s(n) \\ f(n) \\ f(n-1) \end{matrix} \right\} ⎩⎨⎧100pp1qq0⎭⎬⎫n−1∗⎩⎨⎧a+bba⎭⎬⎫=⎩⎨⎧s(n)f(n)f(n−1)⎭⎬⎫
#include NEFU458 Another kind of Fibonacci
{ 1 1 0 0 0 x 2 y 2 2 x y 0 1 0 0 0 x 0 y } n ∗ { s ( 0 ) f 2 ( 1 ) f 2 ( 0 ) f ( 1 ) f ( 0 ) } = { s ( n ) f 2 ( n + 1 ) f 2 ( n ) f ( n + 1 ) f ( n ) } \left\{ \begin{matrix} 1 & 1 & 0 &0 \\ 0 & x^2 & y^2 &2xy \\ 0 & 1 & 0 &0 \\ 0 & x &0 &y \end{matrix} \right\} ^{n}*\left\{ \begin{matrix} s(0) \\ f^2(1) \\ f^2(0) \\ f(1)f(0) \end{matrix} \right\}=\left\{ \begin{matrix} s(n) \\ f^2(n+1) \\ f^2(n) \\ f(n+1)f(n) \end{matrix} \right\} ⎩⎪⎪⎨⎪⎪⎧10001x21x0y20002xy0y⎭⎪⎪⎬⎪⎪⎫n∗⎩⎪⎪⎨⎪⎪⎧s(0)f2(1)f2(0)f(1)f(0)⎭⎪⎪⎬⎪⎪⎫=⎩⎪⎪⎨⎪⎪⎧s(n)f2(n+1)f2(n)f(n+1)f(n)⎭⎪⎪⎬⎪⎪⎫
#include 完结。