线段树模板 | 区间修改,区间求和,区间查询最值
一、线段树简介
线段树本质上是一个二叉树,除了叶子节点之外,其余的父亲节点都有两个儿子;学过数据结构中的二叉树都知道,儿子节点与父亲节点下标的关系;((下标从1开始)设父亲节点下标为p,则左儿子下标为2 * p,右儿子下标为2 * p + 1),线段树在建树的时候就是根据这个简单的结论而递归建树的;
对于每一个非叶子节点而言,都存储着它管辖的子区间的信息;而对于每个叶子节点,都存储着序列中单个元素信息;在工作时,父亲节点和儿子节点相互传递信息可以实现在log2N时间内修改或查询操作;
线段树的基本操作有:单点修改,区间修改,区间查询总和,区间查询最值问题等等;实际上线段树可以用来处理很多符合结合律的操作;
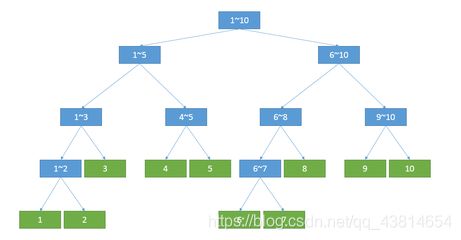
线段树的结构图示
(图片来自互联网QAQ)
二、线段树相关函数代码实现
线段树的用处不同,相关函数的写法也会因此发生改变;
因此此处以洛谷上一题P3372 【模板】线段树 1作为示例讲解解答这题时线段树相关函数的编写;
简述题意:
第一行输入n,m表示序列的长度和操作的次数:
第二行输入n个数表示初始序列
下面m行 有两种操作
第一种操作:将某区间每个数都加上K;
第二种操作:求出某区间的总和;
1.用结构体表示线段树
const int MAXN = 1e5 + 10;
int n;//一般是题目输入的,表示下述序列的大小;
ll a[MAXN];//线段树需要维护的序列
struct tree//线段树结构
{
int l,r;//代表节点维护的区间范围;
ll data; //代表该节点维护的值;
ll lazy; //涉及lazy标记的东西,有时候lazy不止一个(涉及到区间修改时会使用到);
}t[MAXN << 2];//线段树一般开4倍空间,至于为什么嘛,我也不知道,记住就好嘿嘿;
2.递归建立一颗线段树
//此处即是利用到 二叉树中儿子节点与父亲节点下标的关系
//设父亲节点下标为p,则左儿子下标为2 * p,右儿子下标为2 * p + 1
//inline 可以有效防止无需入栈的信息入栈,节省时间和空间
//<< 符号 和 | 符号是利用二进制运算加快速度
inline int lson(int p){return p << 1;}//左儿子;
inline int rson(int p){return p << 1 | 1;}//右儿子;
void build(int p,int l,int r)
{
t[p].l = l,t[p].r = r;//以p为编号的节点维护的区间为[l,r];
if(l == r) //叶子节点存放真实的数值;
{
t[p].data = a[l];
return;
}
int mid = t[p].l + t[p].r >> 1;//以当前区间中点为界建立左右儿子;
build(lson(p),l,mid);//
build(rson(p),mid + 1,r);
//回溯时将其子节点的信息存下来(push_up操作);
t[p].data = t[lson(p)].data + t[rson(p)].data;
}
3.区间更新
push_down操作是区间更新中必要的操作,也是线段树中的重难点;
在push_down操作中,lazy标记正式发挥它的作用;z之所以称之为"懒标记",是因为原本区间修改需要通过先改变叶子节点的值,然后不断的向上递归修改祖先节点直至到达根节点,时间复杂高达O(Nlog2N);但当我们引入了lazy操作之后,区间更新的期望复杂度就降到了**O(log2N)**的级别甚至更低;
怎么使用lazy标记呢?
首先lazy标记的作用是记录每次每个节点要更新的值,然后进行传递式记录:
整个区间被操作,记录在公共祖先节点上;只修改了一部分,那么就记录在这部分的公共祖先上;只改变了自己的话,当然也就只改变自己;
具体看代码吧~
void push_down(int p)//递归到达当前节点;
{
if(t[p].lazy)
{
//如果lazy标记不为0,就将其下传,修改左右儿子维护的值;
t[lson(p)].data += t[p].lazy * (t[lson(p)].r - t[lson(p)].l + 1);
t[rson(p)].data += t[p].lazy * (t[rson(p)].r - t[rson(p)].l + 1);
//接替父亲的任务,等待机会下传;
t[lson(p)].lazy += t[p].lazy;
t[rson(p)].lazy += t[p].lazy;
t[p].lazy = 0;//下传完成,更新lazy为0;
}
}
void update(int p,int l,int r,ll value)
{
if(l <= t[p].l && r >= t[p].r)//区间被覆盖,就修改;
{
t[p].data += value * (t[p].r - t[p].l + 1);
t[p].lazy += value;
return;
}
//如果没有被覆盖,那就需要继续向下找;
push_down(p);//向下更新儿子节点的数据;
//考虑儿子所维护的区间可能因为懒标记的存在而没有修改,因此将懒标记下放;
int mid = t[p].l + t[p].r >> 1;
if(l <= mid)update(lson(p),l,r,value);//覆盖了左儿子就修改左儿子;
if(r > mid)update(rson(p),l,r,value);//覆盖了右儿子就修改右儿子;
t[p].data = t[lson(p)].data + t[rson(p)].data;//向上更新父亲节点的数据;
}
4.区间查询
区间查询的函数是最为简单的,很好理解的,只是将数据进行整合,具体实现看代码~
ll querySum(int p,int l,int r)
{
if(l <= t[p].l && r >= t[p].r)return t[p].data;//覆盖了该区间
push_down(p);//此处的push_down和update函数是一个含义;
ll sum = 0;
int mid = t[p].l + t[p].r >> 1;
if(l <= mid)sum += querySum(lson(p),l,r);//整合左儿子的数据;
if(r > mid)sum += querySum(rson(p),l,r);//整合右儿子的数据;
return sum;//累加答案返回左右儿子的和;
}
到此,线段树区间更新查询的主要函数就写完了;最后贴一份AC的代码;
#include5.区间查询最值
例题poj3264 Balanced Lineup
题目简述:
给出一个长度为n的数列,对于给出的l和r,输出该区间中最大值 - 最小值;
区间查询最值也是线段树最为基本的操作,其实质上也是对数据的整合,仿照着区间查询代码非常容易就可以得出区间查询最值的代码的:
ll query_Max(int p,int l,int r)
{
if(l <= t[p].l && r >= t[p].r)return t[p].Max;//查询区间覆盖了节点的管辖区间直接返回该区间的最大值;
int mid = t[p].l + t[p].r >> 1;
ll maxL = -inf,maxR = -inf;
if(l <= mid)maxL = max(maxL,query_Max(lson(p),l,r));//查询左儿子的最大值;
if(r > mid)maxR = max(maxR,query_Max(rson(p),l,r));//查询右儿子的最大值;
return max(maxL,maxR);//最后返回以此为根中所有子树的最大值;
}
//查询最小值的注释同查询最大值的相似,不再赘述;
ll query_Min(int p,int l,int r)
{
if(l <= t[p].l && r >= t[p].r)return t[p].Min;
int mid = t[p].l + t[p].r >> 1;
ll minL = inf,minR = inf;
if(l <= mid)minL = min(minL,query_Min(lson(p),l,r));
if(r > mid)minR = min(minR,query_Min(rson(p),l,r));
return min(minL,minR);
}
最后的AC代码:
#include三、总结
线段树作为一种极其常用的数据结构,熟练掌握它就显得非常有必要;此文仅仅作为入门级别的线段树,仅仅介绍了线段树的基本用法,线段树的学习还是任重而道远;愿每个努力的人都能得到回报,加油~
参考博文
https://www.luogu.com.cn/blog/pks-LOVING/senior-data-structure-qian-tan-xian-duan-shu-segment-tree