菜鸟观点---图论之最短路BF算法

菜鸟观点之图论BF最短路算法

要开学啦
在匆忙比赛后开始整理行装，准备迈向新的战场，这大概是我人生中最忙碌的两天。

昨天晚上是百度之星的预选赛，抱着死马当活马医的心态，通俗一点就是懒的我对这个比赛并没有抱什么希望，直到比赛前两天还在看图论相关内容，没有准备丝毫的相关内容。

中国的比赛继承了中国人对数学骨子里的重视，无论是hd多校，还是ccpc，又或者是codeM和华为精英挑战赛，数学往往是压轴题，作为一个目睹了郭神一连9天讲课未曾停顿丝毫，讲到ACM中的数学问题的时候却跌落神坛，频频卡壳的入门菜鸟，自知谈夺得第几名这种问题还是为时尚早，唯一抱的希望就是不要在开学前最后一次比赛中爆零。在以前和队友的合作训练中，这种情况频频发生，真的让人感觉不那么良好。

紧张不安的心情让我当了一回香香怪，还是做了一下百度之星预选赛的往年题，第一道是一个非常典型的搜索的题，用BFS写了之后提交却出现了超时的情况，当时心里已经由于预感这道题并没有我想象中的那么简单，但还是硬着头皮改用了DFS回溯法外加可行性剪枝，得到的结果却是Wrong Answer。emmmm上网一搜这道题的确是DFS不假，但是却需要用到状态压缩，emmm我对位逻辑运算的还停留在上次去郑州大学老师那堂课讲的内容，我选择死亡。照这样下去，凉凉夜色为我思念成河~。

不过昨天的比赛还是挺秃然的，1001题是讨论多项式做分母和分子的时候的收敛焦点。原来是用洛必达公式用最高项常数之比算出分数形式的焦点并化简，即分子分母同时除以最大公因数（GCD），这题难度不高，直接拿下。中间出了个小插曲，我把分数的斜线方向搞错了，一直Wrong Answer，卡了我一个小时的时间，后期排出了这个错误，AC! 有了第一题保底，胆子就肥了起来，开始主攻1005题。1005是一个数列求和的题，给一个数字N让求出第N项，看到输入最大是10的12次方的时候我就暗暗说了一声不妙，原先用动态规划记忆，最好的复杂度也只能是O（N）的，10的12次幂的输入就算用O(N)也一定会超时。那这道题一定是O(LogN)或者是常数时间的，可我也没有找到任何可以二分或者是常数化简的办法啊，硬着头皮用dp写完了这题，提交了。

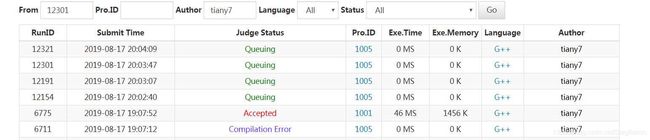
激动人心的时刻到了！当然不是我的答案Accepted了，而是比赛平台HDU的测评机炸了，所有的答案都显示Queuing。那一刻看群里，感觉有种高中课堂停电一般的欢乐，开始战术唠嗑。虽然我知道是超时了，但是直到最后百度的管理员宣布比赛暂停，我的答案都没被批改，我也没想出来任何有效的方法让它不超时。后来问了问高中的微积分老师，hhhhh这题要用到归纳法，高一的我肯定能做出来，然而现在的我，惭愧惭愧，还是得学好数学。

匆忙的一天结束了，看着郑州夜里最后一点灯光，看一眼大玉米，该去上学啦！三个月的清闲时光已经将我放得准备足够充分去更高的舞台上去和大佬们比拼了。各位，勿念！再见啦！最后，送上一句略显直男的关怀的话给大家，再苦，再累，记得喝白开水！

最短路之BF算法
最短路问题作为经典的图论题其实在ICPC里非常常见，顾名思义就是在几个地点里，把走路的花费降至最小的一种算法。如果靠单纯的枚举，时间复杂度恐怕会上O(N^N)，这显然是太过庞大，不可接受。所以之前每次遇到图论最短路的问题都会非常头疼，虽然郭神讲过了，但是自己内心还是对最短路算法有一些恐惧，很多基础的图论题只得跳过。当然，要来的早晚要来，仔细拜读了下郭神的代码，发现其实Bellman Ford算法比起用来计算最小生成树的Prim算法和Kruskal算法并没有难太多，是寡人多虑了hhhhhh

言归正传，BF算法还是很好用的，适用于有向图，即每条边都有明确指向，单向不可逆。这样的图有一个问题亟待解决，就是在克鲁斯卡尔算法中，我们用并查集来避免出现路线绕圈从而陷入死胡同，但是要判断是否有这样的绕圈（我们称之为负权环），我们还是需要用另外的方法判断，这就引入了BF算法。

BF算法，用一句话概括，就是利用动态规划的思想将每个起始点和各个点之间的距离记录下来，并且枚举各个边不断优化（如果一个点的起点加上某一条边的费用小于前面用无论什么方法得到的费用，那么这点就是局部最优的），这样之后，反复把每个点的情况进行枚举。完毕之后，我们再检查一遍，如果有一点，走他，比不走他话费的钱要多，用通俗的话来讲就是花冤枉钱了，那就说明这个图里存在负权环，这就是BF算法的原理，下面不说了，看代码吧，都在注释上了。祝大家有一个愉快的大学生活。以下代码均来自北京大学信息科学院郭炜老师，如果有涉及侵权请联系我删除。

#include 
#include 
#include 
#include 
using namespace std;
#define limit 1000 + 5//代表总大小，开足够大小数组
#define INF 0x3f3f3f3f
void read(int &x){
    char ch = getchar();x = 0;
    for (; ch < '0' || ch > '9'; ch = getchar());
    for (; ch >='0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
}//用getchar方法读取输入方便计算
void readSymbol(char &x){
    char ch = getchar();x = 0;
    for (; ch == ' '; ch = getchar());
    for (; ch != ' '; ch = getchar()) x = getchar();//读到条件的时候会返回
}//用getchar方法读取输入方便计算
/***
 * 这是Bellman Ford算法在POJ3259 （Wormhole）中的运用，大家acm冲压！！！！
 */
struct edge{
    //开一个结构体存放边和所附带的权值
    int from, to , weight;//分别代表了起始点，终点，和权值
    edge():from(0),to(0),weight(0){}//开一个构造函数方便创造数组
    edge(int x , int y , int z):from(x), to(y),weight(z){}//有参构造方法方便赋值
};
int kase, n , m, w;//kase代表testcase数量，n代表点的数量，m代表正权边数量，w代表负权边数量
vectorEdges;//使用vector构造一个邻接表，和deque一样，vector是用数组实现的，而且大小是可以变化的
//运算符加快了边的处理，所以用一个vector储存
int dist[limit];//这里开足够大小的数组存放距离，鉴于题中所给的条件，给1000另外加上5是一个比较保险的数字
//推荐大家用宏定义或者常数定义limit以增加代码的可操作性
bool bellmanFord(int start){//前方高能！！！！这里不得不提一下命名，图论里的变量多如牛毛，如果不是像郭神一样的大佬或者是
    //资深的OI选手还是建议不要吝啬变量名字的长度，有时候很严重的bug排除到最后发现是某一两个变量放反了，或者是用错了/前面定义过导致的
    //所以我这里用了start，表示bellman ford区别于构建最小生成树的Kruskal算法，是从任意一点开始的，不存在优先性
   memset(dist,0 , n + 1);//这里dist数组是用来储存到每个点的最短距离的，在没有开始探索之前，初始为无穷大
   //另外，memset函数的执行时间复杂度是线性的，但是如果常数较大仍然有拉慢甚至tle的风险，所以不建议用sizeof()去设置大小
    //代表目前没有可行最短路径到这个点，为何能算最短路？这是一个非常通俗易懂的逻辑，我不管用什么方法，走什么路径取得了
    //比当前这一点所存距离更小的距离，那么我一定是有办法在给定最小值内走到这个点的，因此我不需要关心这个最小值是怎么来的，毋庸置疑，这个逻辑是成立的
    dist[start] = 0;//出发点为start，自己到自己肯定是0hhhhhh
    for(int i = 1 ; i < n ; ++i){//这一层循环枚举每一个边,执行n - 1次
        for(int j = 0 ; j < Edges.size(); ++j){//这一层是用来探查每一条边的情况的
            int vs = Edges[j].from, ve = Edges[j].to, weight = Edges[j].weight;
            //vs代表了起始点，ve代表了终点，weight则是路的权值（费用）
            if(dist[vs] != INF && dist[vs] + weight < dist[ve]){
                //这里，像上面说的一样，如果从start到初始点的局部最小距离已经求出，而加上这条边的权值到终点ve的距离小于目前到ve的所有可能
                //路径的最短的那一条，说明了，当前探索的这一条可以替代dist[ve]成为最优解，那么就替换掉它
                dist[ve] = dist[vs] + weight;//替换更新
            }
        }
    }
    for(int i = 0 ; i < Edges.size(); ++i){
        int vs = Edges[i].from, ve = Edges[i].to, weight = Edges[i].weight;//同理不再解释
        if(dist[vs] != INF && dist[vs] + weight < dist[ve]){
            //如果我在求完这一点之后仍然能找到更短的路径，就代表在之前的探索中，存在某一点，或者某一条边
            //使我经过这一点不如不经过这一点，那那一点肯定就是负权回路边
            return true;//代表有负权回路边，在这题里是可达到（INF），那就返回
        }
    }
    return false;//没找到负权回路边,在这题里是不可以达到
}
int main(){
    scanf("%d" , &kase);//test case数目
    while(kase--){
        scanf("%d%d%d", &n, &m, &w);//scanf是C语言的特性残留，但是读入速度是cin的三倍
        for(int i = 0 ; i < m ; ++i){
            int vs, ve, weight;
            scanf("%d%d%d", &vs, &ve, &weight);
            Edges.push_back(edge(vs,ve,weight));
            Edges.push_back(edge(ve,vs,weight));//因为在此处m代表的是双向边的数量，所以肯定要添加两条边
        }
        for(int i = 0 ; i < w ; ++i){
            int vs, ve, weight;
            scanf("%d%d%d" , &vs, &ve, &weight);
            Edges.push_back(edge(vs,ve,-weight));//权值是负的
        }
        if(bellmanFord(1)){
            printf("YES\n");//如果从1可以到达任何一个点
        }else{
            printf("NO\n");//如果不能到达
        }
        Edges.clear();//敲黑板！！！这里一定记得，在vjudge上，这里是要跑很多组数据的，如果没有及时清空，会对后面的
        //判断产生干扰，明明写对了，但也会wrong answer，所以记得清空！！！！
        //大功告成了hhhh
    }
}