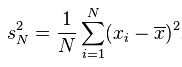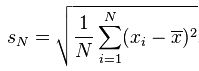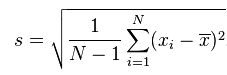- QQ群采集助手,精准引流必备神器
2401_87347160
其他经验分享
功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具,它通过关键词搜索功能,帮助用户快速找到相关的微信群,并提供筛选是否需要验证的群组的功能。主要功能关键词搜索:用户可以输入关键词,工具将自动查找包含该关键词的微信群。筛选功能:工具提供筛选机制,用户可以选择是否只显示需要验证或不需要验证的群组。精准引流:通过上述功能,用户可以更精准地找到目标群组,进行有效的引流操作。3.设备需求该工具可以
- 关于沟通这件事,项目经理不需要每次都面对面进行
流程大师兄
很多项目经理都会遇到这样的问题,项目中由于事情太多,根本没有足够的时间去召开会议,那在这种情况下如何去有效地管理项目中的利益相关者?当然,不建议电子邮件也不需要开会的话,建议可以采取下面几种方式来形成有效的沟通,这几种方式可以帮助你努力的通过各种办法来保持和各方面的联系。项目经理首先要问自己几个问题,项目中哪些利益相关者是必须要进行沟通的?可以列出项目中所有的利益相关者清单,同时也整理出项目中哪些
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
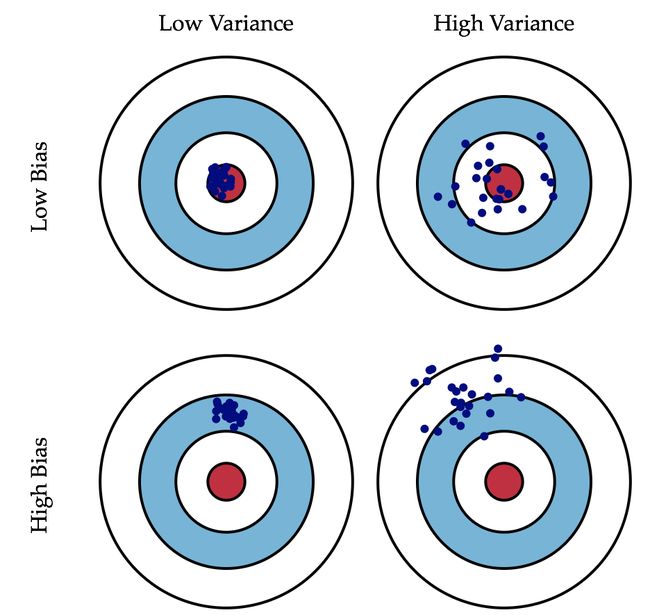
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- element实现动态路由+面包屑
软件技术NINI
vue案例vue.js前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件,它用于显示当前页面的路径,帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中,如果你已经安装了ElementUI,就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例:安装ElementUI(如果你还没有安装的话):你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
- 理解Gunicorn:Python WSGI服务器的基石
范范0825
ipythonlinux运维
理解Gunicorn:PythonWSGI服务器的基石介绍Gunicorn,全称GreenUnicorn,是一个为PythonWSGI(WebServerGatewayInterface)应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具,Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置,帮助初学者快速上手。1.什么是Gunico
- 学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
- 绘本讲师训练营【24期】8/21阅读原创《独生小孩》
1784e22615e0
24016-孟娟《独生小孩》图片发自App今天我想分享一个蛮特别的绘本,讲的是一个特殊的群体,我也是属于这个群体,80后的独生小孩。这是一本中国绘本,作者郭婧,也是一个80厚。全书一百多页,均为铅笔绘制,虽然为黑白色调,但并不显得沉闷。全书没有文字,犹如“默片”,但并不影响读者对该作品的理解,反而显得神秘,梦幻,給读者留下想象的空间。作者在前蝴蝶页这样写到:“我更希望父母和孩子一起分享这本书,使他
- 我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动
李蕾1229
为促进我校教师专业发展,发挥骨干教师的引领带头作用,11月6日下午,我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动。图片发自App会议由教师发展处李蕾主任主持,首先,由范校长宣读新老教师结对名单及双方承担职责。随后,两位新调入教师陈玉萍、莫正杰分别和他们的师傅鲍元美、刘召彬老师签订了师徒结对协议书。图片发自App图片发自App师徒拥抱、握手。有了师傅就有了目标有了方向,相信两位新教师在师
- 向内而求
陈陈_19b4
10月27日,阴。阅读书目:《次第花开》。作者:希阿荣博堪布,是当今藏传佛家宁玛派最伟大的上师法王,如意宝晋美彭措仁波切颇具影响力的弟子之一。多年以来,赴海内外各地弘扬佛法,以正式授课、现场开示、发表文章等多种方法指导佛学弟子修行佛法。代表作《寂静之道》、《生命这出戏》、《透过佛法看世界》自出版以来一直是佛教类书籍中的畅销书。图片发自App金句:1.佛陀说,一切痛苦的根源在于我们长期以来对自身及外
- html 中如何使用 uniapp 的部分方法
某公司摸鱼前端
htmluni-app前端
示例代码:Documentconsole.log(window);效果展示:好了,现在就可以uni.使用相关的方法了
- 《大清方方案》| 第二话
谁佐清欢
和珅究竟说了些什么?竟能令堂堂九五之尊龙颜失色!此处暂且按下不表;单说这位乾隆皇帝,果真不愧是康熙从小带过的,一旦决定了要做的事,便杀伐决断毫不含糊。他当即亲自拟旨,着令和珅为钦差大臣,全权负责处理方方事件,并钦赐尚方宝剑,遇急则三品以下官员可先斩后奏。和珅身负皇上重托,岂敢有半点怠慢,当夜即率领相关人等,马不停蹄杀奔江汉。这一路上,和珅的几位幕僚一直在商讨方方事件的处置方案。有位年轻幕僚建议快刀
- Python中os.environ基本介绍及使用方法
鹤冲天Pro
#Pythonpython服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
- 水泥质量纠纷案代理词
徐宝峰律师
贵州领航建设有限公司诉贵州纳雍隆庆乌江水泥有限公司产品质量纠纷案代理词尊敬的审判长、审判员:贵州千里律师事务所接受被告贵州纳雍隆庆乌江水泥有限公司的委托,指派我担任其诉讼代理人,参加本案的诉讼活动。下面,我结合本案事实和相关法律规定发表如下代理意见,供合议庭评议案件时参考:原告应当举证证明其遭受的损失与被告生产的水泥质量的因果关系。首先水泥是一种粉状水硬性无机胶凝材料。加水搅拌后成浆体,能在空气中
- 怎么起诉借钱不还的人?怎样起诉欠款不还的人?
影子爱学习
怎么起诉借钱不还的人?怎样起诉欠款不还的人?如果遇到难以解决的法律问题,我们可以匹配专业律师。例如:婚姻家庭(离婚纠纷)、刑事辩护、合同纠纷、债权债务、房产(继承)纠纷、交通事故、劳动争议、人身损害、公司相关法律事务(法律顾问)等咨询推荐手机/微信:15633770876【全国案件皆可】借钱不还起诉对方需要哪些资料起诉欠钱不还的,一般需要的材料包括以下这些:借据、收据、欠条、付款凭证等证据,以及向
- 第四天旅游线路预览——从换乘中心到喀纳斯湖
陟彼高冈yu
基于Googleearthstudio的旅游规划和预览旅游
第四天:从贾登峪到喀纳斯风景区入口,晚上住宿贾登峪;换乘中心有4路车,喀纳斯①号车,去喀纳斯湖,路程时长约5分钟;将上面的的行程安排进行动态展示,具体步骤见”Googleearthstudio进行动态轨迹显示制作过程“、“Googleearthstudio入门教程”和“Googleearthstudio进阶教程“相关内容,得到行程如下所示:Day4-2-480p
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- LLM 词汇表
落难Coder
LLMsNLP大语言模型大模型llama人工智能
Contextwindow“上下文窗口”是指语言模型在生成新文本时能够回溯和参考的文本量。这不同于语言模型训练时所使用的大量数据集,而是代表了模型的“工作记忆”。较大的上下文窗口可以让模型理解和响应更复杂和更长的提示,而较小的上下文窗口可能会限制模型处理较长提示或在长时间对话中保持连贯性的能力。Fine-tuning微调是使用额外的数据进一步训练预训练语言模型的过程。这使得模型开始表示和模仿微调数
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 深入理解 MultiQueryRetriever:提升向量数据库检索效果的强大工具
nseejrukjhad
数据库python
深入理解MultiQueryRetriever:提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域,高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用,但仍存在一些局限性。本文将介绍一种创新的解决方案:MultiQueryRetriever,它通过自动生成多个查询视角来增强检索效果,提高结果的相关性和多样性。MultiQueryRetriever的工
- 春季养肝正当时
dxn悟
重温快乐2023年2月4日立春。春天来了,春暖花开,小鸟欢唱,那在这样的季节我们如何养肝呢?自然界的春季对应中医五行的木,人体五脏肝属木,“木曰曲直”,是以树干曲曲直直地向上、向外伸长舒展的生发姿态,来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念,肝五行属木,喜条达,主疏泄,与春天相应,所以春天最适合养肝。养肝首先要少生气,因为肝喜条达恶抑郁。人体五志肝为怒,生气发怒最
- python八股文面试题分享及解析(1)
Shawn________
python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果:21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型,不仅仅改变
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- MYSQL面试系列-04
king01299
面试mysql面试
MYSQL面试系列-0417.关于redolog和binlog的刷盘机制、redolog、undolog作用、GTID是做什么的?innodb_flush_log_at_trx_commit及sync_binlog参数意义双117.1innodb_flush_log_at_trx_commit该变量定义了InnoDB在每次事务提交时,如何处理未刷入(flush)的重做日志信息(redolog)。它
- 每日算法&面试题,大厂特训二十八天——第二十天(树)
肥学
⚡算法题⚡面试题每日精进java算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题,最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧!!特别介绍小白练手专栏,适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
- node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
- CX8836:小体积大功率升降压方案推荐(附Demo设计指南)
诚芯微科技
社交电子
CX8836是一颗同步四开关单向升降压控制器,在4.5V-40V宽输入电压范围内稳定工作,持续负载电流10A,能够在输入高于或低于输出电压时稳定调节输出电压,可适用于USBPD快充、车载充电器、HUB、汽车启停系统、工业PC电源等多种升降压应用场合,为大功率TYPE-CPD车载充电器提供最优解决方案。提供CX8836Demo测试、CX8836样品申请及CX8836方案开发技术支持。CX8836同升
- 如何成为段子手
欣雅阅读
我是一个尬聊大师,与朋友聊天经常把话题聊死,留我一个人在群里,望着自己打下的最后一句话无语凝噎。看到风趣幽默的朋友与人聊天,很是艳羡,觉得自己何时才能成为这样的段子手呢?一、段子是什么?“段子”一词在百度百科上的解释:本是相声中的一个艺术术语,指的是相声作品中一节或一段艺术内容。我的理解:段子就是一些搞笑的故事或者笑话。二、为什么要会说段子?不知道大家有没有这样的朋友,本来很无趣的聚会,只要有他参
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- python os 环境变量
CV矿工
python开发语言numpy
环境变量:环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里,比如数据库密码,个人账户密码,如果写进自己本机的环境变量里,程序用的时候通过os.environ.get()取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量:os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
- java杨辉三角
3213213333332132
java基础
package com.algorithm;
/**
* @Description 杨辉三角
* @author FuJianyong
* 2015-1-22上午10:10:59
*/
public class YangHui {
public static void main(String[] args) {
//初始化二维数组长度
int[][] y
- 《大话重构》之大布局的辛酸历史
白糖_
重构
《大话重构》中提到“大布局你伤不起”,如果企图重构一个陈旧的大型系统是有非常大的风险,重构不是想象中那么简单。我目前所在公司正好对产品做了一次“大布局重构”,下面我就分享这个“大布局”项目经验给大家。
背景
公司专注于企业级管理产品软件,企业有大中小之分,在2000年初公司用JSP/Servlet开发了一套针对中
- 电驴链接在线视频播放源码
dubinwei
源码电驴播放器视频ed2k
本项目是个搜索电驴(ed2k)链接的应用,借助于磁力视频播放器(官网:
http://loveandroid.duapp.com/ 开放平台),可以实现在线播放视频,也可以用迅雷或者其他下载工具下载。
项目源码:
http://git.oschina.net/svo/Emule,动态更新。也可从附件中下载。
项目源码依赖于两个库项目,库项目一链接:
http://git.oschina.
- Javascript中函数的toString()方法
周凡杨
JavaScriptjstoStringfunctionobject
简述
The toString() method returns a string representing the source code of the function.
简译之,Javascript的toString()方法返回一个代表函数源代码的字符串。
句法
function.
- struts处理自定义异常
g21121
struts
很多时候我们会用到自定义异常来表示特定的错误情况,自定义异常比较简单,只要分清是运行时异常还是非运行时异常即可,运行时异常不需要捕获,继承自RuntimeException,是由容器自己抛出,例如空指针异常。
非运行时异常继承自Exception,在抛出后需要捕获,例如文件未找到异常。
此处我们用的是非运行时异常,首先定义一个异常LoginException:
/**
* 类描述:登录相
- Linux中find常见用法示例
510888780
linux
Linux中find常见用法示例
·find path -option [ -print ] [ -exec -ok command ] {} \;
find命令的参数;
- SpringMVC的各种参数绑定方式
Harry642
springMVC绑定表单
1. 基本数据类型(以int为例,其他类似):
Controller代码:
@RequestMapping("saysth.do")
public void test(int count) {
}
表单代码:
<form action="saysth.do" method="post&q
- Java 获取Oracle ROWID
aijuans
javaoracle
A ROWID is an identification tag unique for each row of an Oracle Database table. The ROWID can be thought of as a virtual column, containing the ID for each row.
The oracle.sql.ROWID class i
- java获取方法的参数名
antlove
javajdkparametermethodreflect
reflect.ClassInformationUtil.java
package reflect;
import javassist.ClassPool;
import javassist.CtClass;
import javassist.CtMethod;
import javassist.Modifier;
import javassist.bytecode.CodeAtt
- JAVA正则表达式匹配 查找 替换 提取操作
百合不是茶
java正则表达式替换提取查找
正则表达式的查找;主要是用到String类中的split();
String str;
str.split();方法中传入按照什么规则截取,返回一个String数组
常见的截取规则:
str.split("\\.")按照.来截取
str.
- Java中equals()与hashCode()方法详解
bijian1013
javasetequals()hashCode()
一.equals()方法详解
equals()方法在object类中定义如下:
public boolean equals(Object obj) {
return (this == obj);
}
很明显是对两个对象的地址值进行的比较(即比较引用是否相同)。但是我们知道,String 、Math、I
- 精通Oracle10编程SQL(4)使用SQL语句
bijian1013
oracle数据库plsql
--工资级别表
create table SALGRADE
(
GRADE NUMBER(10),
LOSAL NUMBER(10,2),
HISAL NUMBER(10,2)
)
insert into SALGRADE values(1,0,100);
insert into SALGRADE values(2,100,200);
inser
- 【Nginx二】Nginx作为静态文件HTTP服务器
bit1129
HTTP服务器
Nginx作为静态文件HTTP服务器
在本地系统中创建/data/www目录,存放html文件(包括index.html)
创建/data/images目录,存放imags图片
在主配置文件中添加http指令
http {
server {
listen 80;
server_name
- kafka获得最新partition offset
blackproof
kafkapartitionoffset最新
kafka获得partition下标,需要用到kafka的simpleconsumer
import java.util.ArrayList;
import java.util.Collections;
import java.util.Date;
import java.util.HashMap;
import java.util.List;
import java.
- centos 7安装docker两种方式
ronin47
第一种是采用yum 方式
yum install -y docker
- java-60-在O(1)时间删除链表结点
bylijinnan
java
public class DeleteNode_O1_Time {
/**
* Q 60 在O(1)时间删除链表结点
* 给定链表的头指针和一个结点指针(!!),在O(1)时间删除该结点
*
* Assume the list is:
* head->...->nodeToDelete->mNode->nNode->..
- nginx利用proxy_cache来缓存文件
cfyme
cache
user zhangy users;
worker_processes 10;
error_log /var/vlogs/nginx_error.log crit;
pid /var/vlogs/nginx.pid;
#Specifies the value for ma
- [JWFD开源工作流]JWFD嵌入式语法分析器负号的使用问题
comsci
嵌入式
假如我们需要用JWFD的语法分析模块定义一个带负号的方程式,直接在方程式之前添加负号是不正确的,而必须这样做:
string str01 = "a=3.14;b=2.71;c=0;c-((a*a)+(b*b))"
定义一个0整数c,然后用这个整数c去
- 如何集成支付宝官方文档
dai_lm
android
官方文档下载地址
https://b.alipay.com/order/productDetail.htm?productId=2012120700377310&tabId=4#ps-tabinfo-hash
集成的必要条件
1. 需要有自己的Server接收支付宝的消息
2. 需要先制作app,然后提交支付宝审核,通过后才能集成
调试的时候估计会真的扣款,请注意
- 应该在什么时候使用Hadoop
datamachine
hadoop
原帖地址:http://blog.chinaunix.net/uid-301743-id-3925358.html
存档,某些观点与我不谋而合,过度技术化不可取,且hadoop并非万能。
--------------------------------------------万能的分割线--------------------------------
有人问我,“你在大数据和Hado
- 在GridView中对于有外键的字段使用关联模型进行搜索和排序
dcj3sjt126com
yii
在GridView中使用关联模型进行搜索和排序
首先我们有两个模型它们直接有关联:
class Author extends CActiveRecord {
...
}
class Post extends CActiveRecord {
...
function relations() {
return array(
'
- 使用NSString 的格式化大全
dcj3sjt126com
Objective-C
格式定义The format specifiers supported by the NSString formatting methods and CFString formatting functions follow the IEEE printf specification; the specifiers are summarized in Table 1. Note that you c
- 使用activeX插件对象object滚动有重影
蕃薯耀
activeX插件滚动有重影
使用activeX插件对象object滚动有重影 <object style="width:0;" id="abc" classid="CLSID:D3E3970F-2927-9680-BBB4-5D0889909DF6" codebase="activex/OAX339.CAB#
- SpringMVC4零配置
hanqunfeng
springmvc4
基于Servlet3.0规范和SpringMVC4注解式配置方式,实现零xml配置,弄了个小demo,供交流讨论。
项目说明如下:
1.db.sql是项目中用到的表,数据库使用的是oracle11g
2.该项目使用mvn进行管理,私服为自搭建nexus,项目只用到一个第三方 jar,就是oracle的驱动;
3.默认项目为零配置启动,如果需要更改启动方式,请
- 《开源框架那点事儿16》:缓存相关代码的演变
j2eetop
开源框架
问题引入
上次我参与某个大型项目的优化工作,由于系统要求有比较高的TPS,因此就免不了要使用缓冲。
该项目中用的缓冲比较多,有MemCache,有Redis,有的还需要提供二级缓冲,也就是说应用服务器这层也可以设置一些缓冲。
当然去看相关实现代代码的时候,大致是下面的样子。
[java]
view plain
copy
print
?
public vo
- AngularJS浅析
kvhur
JavaScript
概念
AngularJS is a structural framework for dynamic web apps.
了解更多详情请见原文链接:http://www.gbtags.com/gb/share/5726.htm
Directive
扩展html,给html添加声明语句,以便实现自己的需求。对于页面中html元素以ng为前缀的属性名称,ng是angular的命名空间
- 架构师之jdk的bug排查(一)---------------split的点号陷阱
nannan408
split
1.前言.
jdk1.6的lang包的split方法是有bug的,它不能有效识别A.b.c这种类型,导致截取长度始终是0.而对于其他字符,则无此问题.不知道官方有没有修复这个bug.
2.代码
String[] paths = "object.object2.prop11".split("'");
System.ou
- 如何对10亿数据量级的mongoDB作高效的全表扫描
quentinXXZ
mongodb
本文链接:
http://quentinXXZ.iteye.com/blog/2149440
一、正常情况下,不应该有这种需求
首先,大家应该有个概念,标题中的这个问题,在大多情况下是一个伪命题,不应该被提出来。要知道,对于一般较大数据量的数据库,全表查询,这种操作一般情况下是不应该出现的,在做正常查询的时候,如果是范围查询,你至少应该要加上limit。
说一下,
- C语言算法之水仙花数
qiufeihu
c算法
/**
* 水仙花数
*/
#include <stdio.h>
#define N 10
int main()
{
int x,y,z;
for(x=1;x<=N;x++)
for(y=0;y<=N;y++)
for(z=0;z<=N;z++)
if(x*100+y*10+z == x*x*x
- JSP指令
wyzuomumu
jsp
jsp指令的一般语法格式: <%@ 指令名 属性 =”值 ” %>
常用的三种指令: page,include,taglib
page指令语法形式: <%@ page 属性 1=”值 1” 属性 2=”值 2”%>
include指令语法形式: <%@include file=”relative url”%> (jsp可以通过 include