【关于四足机器人那些事】腿部运动学建模(三维)
本篇将会三维空间中,对四足机器人的腿部进行数学建模,求解器正逆运动学解,包含详细公式推导与计算
首先,我们来看三维空间中简图:

其中a表示髋关节距离主体得偏移,L1,L2共面,与a保持垂直关系,[x,y,z]表示足端相对于髋关节的位置,为了更容易大家理解,我们将视角转换到不同的视图当中去计算几何关系。
一、正视图:
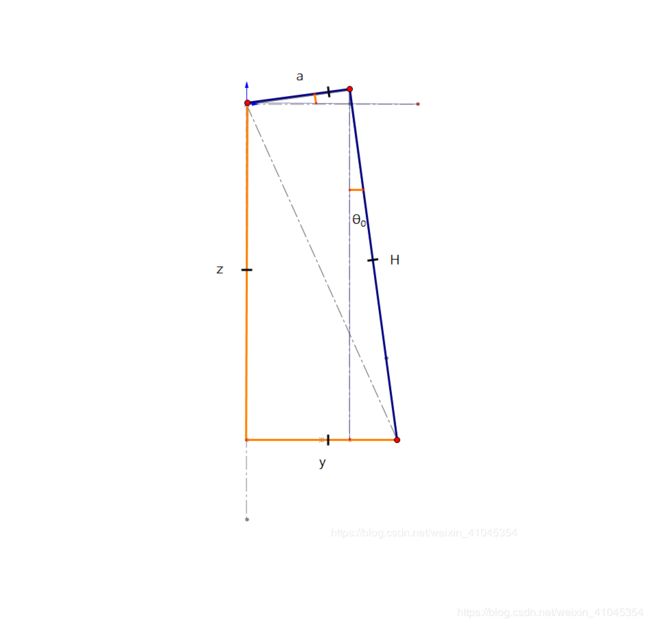
首先来回一下小学知识:
- 互余:如果两个锐角的和等于90度,那么这两个锐角互为余角
通过互余我们可以证明a与y轴的夹角与图中所示 θ 0 \theta_0 θ0相等。通过其数量关系,我们可以得出:
1、正解(已知 θ 0 \theta_0 θ0)
z = − H cos ( θ 0 ) + a sin ( θ 0 ) (1-1) z = -H\cos(\theta_0) + a\sin(\theta_0) \tag{1-1} z=−Hcos(θ0)+asin(θ0)(1-1)
y = a cos ( θ 0 ) + H sin ( θ 0 ) (1-2) y = a\cos(\theta_0) + H\sin(\theta_0) \tag{1-2} y=acos(θ0)+Hsin(θ0)(1-2)
此时,我们只要求出 H H H,即可得到 z z z与 y y y的值
2、逆解(已知x,y,z)
H 2 = z 2 + y 2 − a 2 (2-1) H^2 = z^2 + y^2 - a^2 \tag{2-1} H2=z2+y2−a2(2-1)
θ 0 = a t a n 2 ( H , ∣ z ∣ ) − a t a n 2 ( ∣ z ∣ , y ) (2-2) \theta_0 = atan2(H, |z|) - atan2(|z|, y) \tag{2-2} θ0=atan2(H,∣z∣)−atan2(∣z∣,y)(2-2)
在已知xyz的情况下,通过勾股定理我们能够轻易求出 H H H,在正视图我们需要的公式就这么多,接下来转到右视图
右视图
虽说是右视图,但我们最好不要将其想象成水平向右观看的视图,这里的右视图指的是L1,L2所在平面的视图。这里其实跟二维情况下无疑。H的长度相当于原本的Y轴上的距离。这里就不再重新推导,详情请查看文章
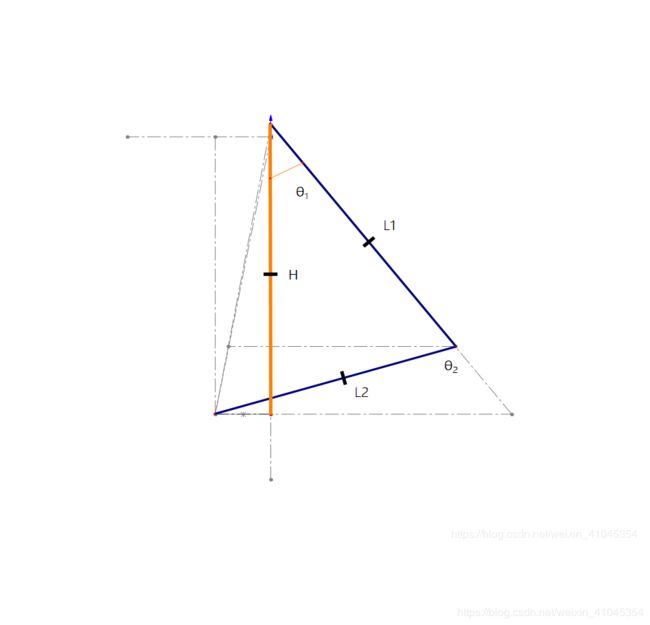
1、正解(已知 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2)
此时 H H H是在L1,L2组成的平面当中,如果空间感比较好的小伙伴应该会发现这时候其实跟二维情况下的几何模型是一致的。因此我们有以下关系:
H = L 1 cos ( θ 1 ) + L 2 cos ( θ 1 + θ 2 ) (1-3) H = L_1\cos(\theta_1) + L_2\cos(\theta_1+\theta_2) \tag{1-3} H=L1cos(θ1)+L2cos(θ1+θ2)(1-3)
x = L 1 sin ( θ 1 ) + L 2 sin ( θ 1 + θ 2 ) (1-4) x = L_1\sin(\theta_1) + L_2\sin(\theta_1+\theta_2) \tag{1-4} x=L1sin(θ1)+L2sin(θ1+θ2)(1-4)
2、逆解(已知xyz)
c 2 = − L 1 2 − L 2 2 + x 2 + H 2 ) 2 L 1 L 2 c_2 = \frac{-L_1^2 - L_2 ^2 + x ^2 + H ^2)}{2 L1 L2} c2=2L1L2−L12−L22+x2+H2)
s 2 = 1 − c 2 2 s_2 = \sqrt{1-c_2^2} s2=1−c22
θ 2 = a t a n 2 ( s 2 , c 2 ) \theta_2 = atan2(s_2, c_2) θ2=atan2(s2,c2)
θ 1 = a t a n 2 ( − z , x ) − a t a n 2 ( L 2 s 2 , L 1 + L 2 ∗ c 2 ) \theta_1 = atan2(-z_, x) - atan2(L_2 s_2, L_1 + L_2 * c2) θ1=atan2(−z,x)−atan2(L2s2,L1+L2∗c2)
整理
我们将所有公式整理一下:
1、正解
H = L 1 cos ( θ 1 ) + L 2 cos ( θ 1 + θ 2 ) (1-3) H = L_1\cos(\theta_1) + L_2\cos(\theta_1+\theta_2) \tag{1-3} H=L1cos(θ1)+L2cos(θ1+θ2)(1-3)
x = L 1 sin ( θ 1 ) + L 2 sin ( θ 1 + θ 2 ) (1-4) x = L_1\sin(\theta_1) + L_2\sin(\theta_1+\theta_2) \tag{1-4} x=L1sin(θ1)+L2sin(θ1+θ2)(1-4)
z = − H cos ( θ 0 ) + a sin ( θ 0 ) (1-1) z = -H\cos(\theta_0) + a\sin(\theta_0) \tag{1-1} z=−Hcos(θ0)+asin(θ0)(1-1)
y = a cos ( θ 0 ) + H sin ( θ 0 ) (1-2) y = a\cos(\theta_0) + H\sin(\theta_0) \tag{1-2} y=acos(θ0)+Hsin(θ0)(1-2)
2、逆解
H 2 = z 2 + y 2 − a 2 H^2 = z^2 + y^2 - a^2 H2=z2+y2−a2
θ 0 = a t a n 2 ( H , ∣ z ∣ ) − a t a n 2 ( ∣ z ∣ , y ) \theta_0 = atan2(H, |z|) - atan2(|z|, y) θ0=atan2(H,∣z∣)−atan2(∣z∣,y)
c 2 = − L 1 2 − L 2 2 + x 2 + H 2 ) 2 L 1 L 2 c_2 = \frac{-L_1^2 - L_2 ^2 + x ^2 + H ^2)}{2 L1 L2} c2=2L1L2−L12−L22+x2+H2)
s 2 = 1 − c 2 2 s_2 = \sqrt{1-c_2^2} s2=1−c22
θ 2 = a t a n 2 ( s 2 , c 2 ) \theta_2 = atan2(s_2, c_2) θ2=atan2(s2,c2)
θ 1 = a t a n 2 ( − z , x ) − a t a n 2 ( L 2 s 2 , L 1 + L 2 ∗ c 2 ) \theta_1 = atan2(-z_, x) - atan2(L_2 s_2, L_1 + L_2 * c2) θ1=atan2(−z,x)−atan2(L2s2,L1+L2∗c2)
同样,需要根据机器人各个关节的初始角度对 θ 0 , θ 1 , θ 2 \theta_0, \theta_1, \theta_2 θ0,θ1,θ2进行一定相加减