遗传算法
1.遗传算法简介
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是在20世纪六七十年代由美国密歇根大学的 Holland教授创立。60年代初,Holland在设计人工自适应系统时提出应借鉴遗传学基本原理模拟生物自然进化的方法。1975年, Holland出版了第一本系统阐述遗传算法基本理论和方法的专著,其中提出了遗传算法理论研究和发展中最重要的模式理论( schemata theory)。因此,一般认为1975年是遗传算法的诞生年。同年, de jong完成了大量基于遗传算法思想的纯数值函数优化计算实验的博士论文,为遗传算法及其应用打下了坚实的基础。1989年, Goldberg的著作对遗传算法做了全面系统的总结和论述,奠定了现代遗传算法的基础。
2.算法基本思想
遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
3.遗传算法的基本流程
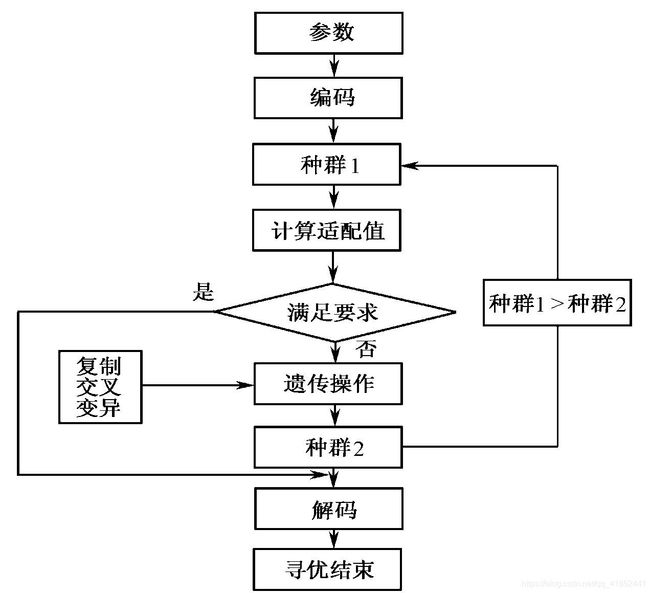
(1)初始化:设置进化代数计数器,设置最大进化代数,随机生成个个体作为初始群体。
(2)个体评价:计算群体中各个个体的适应度。
(3)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
(4)交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
(5)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。
(6)群体经过选择、交叉、变异运算之后得到下一代群体。
(7)终止条件判断:若,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
4.代码运行实现
(1)代码
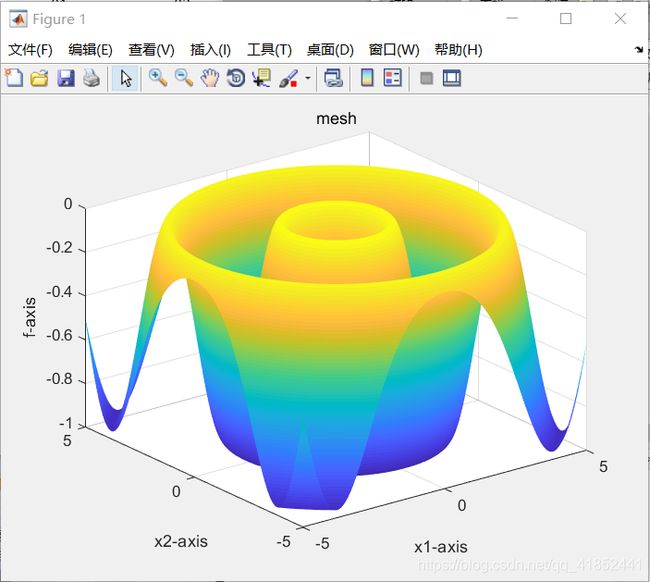
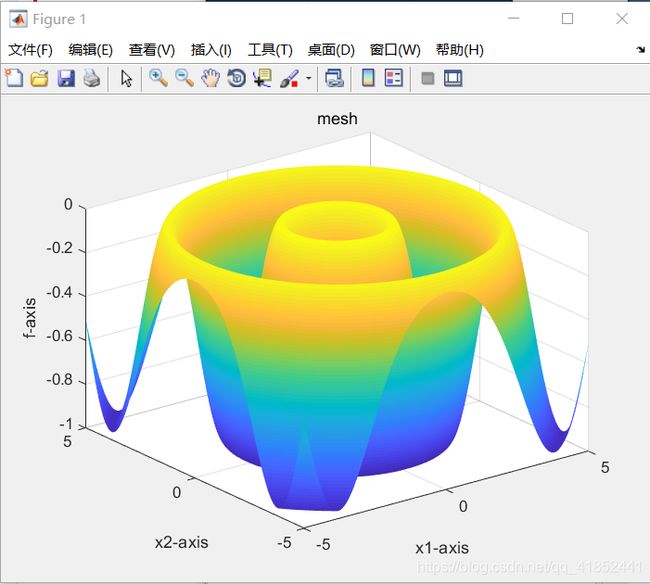
代码由三个适应度函数构成分别为:Griewank,Rastrigin,Schaffer。用遗传算法计算出函数的全局最小值。
GA.m
% Optimizing a function using Simple Genetic Algorithm with elitist preserved
%Max f(x1,x2)=100*(x1*x1-x2).^2+(1-x1).^2; -2.0480<=x1,x2<=2.0480
%下面为代码。函数最大值为3904.9262,此时两个参数均为-2.0480,有时会出现局部极值,此时一个参数为-2.0480,一个为2.0480。变
%异概率pm=0.05,交叉概率pc=0.8。
clc;clear all;
format long;%设定数据显示格式
%初始化参数
T=500;%仿真代数
N=80;% 群体规模
pm=0.05;pc=0.8;%交叉变异概率
umax=30;umin=-30;%参数取值范围
L=10;%单个参数字串长度,总编码长度Dim*L
Dim=5;%Dim维空间搜索
bval=round(rand(N,Dim*L));%初始种群,round函数为四舍五入
bestv=-inf;%最优适应度初值
funlabel=2; %选择待优化的函数,1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(funlabel);%画出待优化的函数,只画出二维情况作为可视化输出
%迭代开始
for ii=1:T
%解码,计算适应度
for i=1:N %对每一代的第i个粒子
for k=1:Dim
y(k)=0;
for j=1:1:L %从1到L,每次加以1
y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值,例如y1是第一维
end
x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
end
% obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数
obj(i)=fun(x,funlabel);
xx(i,:)=x;
end
func=obj;%目标函数转换为适应度函数
p=func./sum(func);
q=cumsum(p);%累加
[fmax,indmax]=max(func);%求当代最佳个体
if fmax>=bestv
bestv=fmax;%到目前为止最优适应度值
bvalxx=bval(indmax,:);%到目前为止最佳位串
optxx=xx(indmax,:);%到目前为止最优参数
end
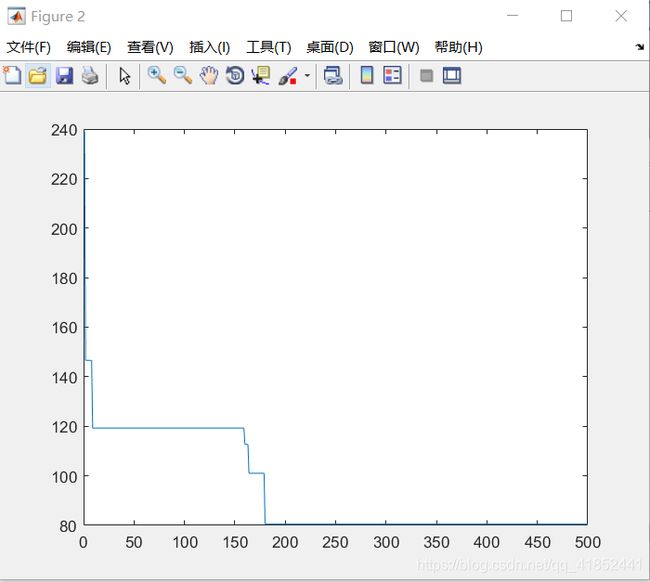
Bfit1(ii)=bestv; % 存储每代的最优适应度
%%%%遗传操作开始
%轮盘赌选择
for i=1:(N-1)
r=rand;
tmp=find(r<=q);
newbval(i,:)=bval(tmp(1),:);
end
newbval(N,:)=bvalxx;%最优保留
bval=newbval;
%单点交叉
for i=1:2:(N-1)
cc=rand;
if ccDrawfunc.m
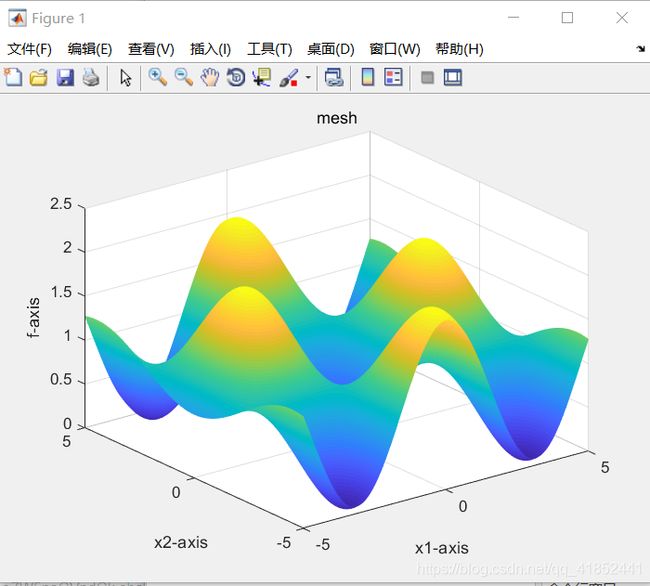
function Drawfunc(label)
x=-5:0.05:5;%41列的向量
if label==1
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
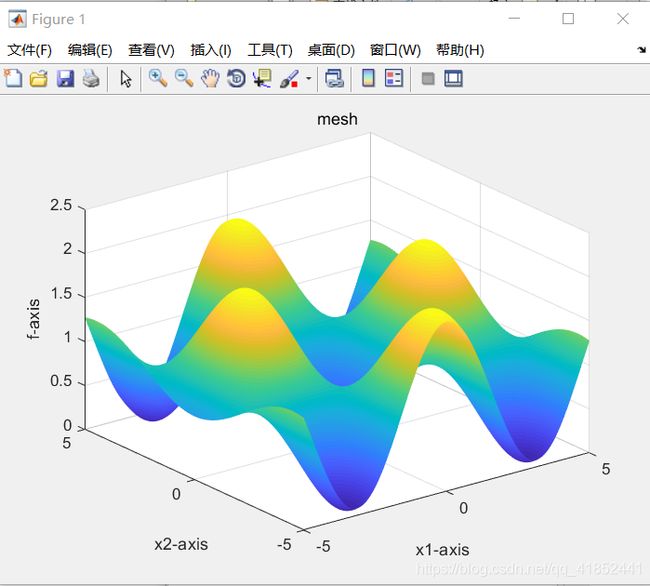
if label==2
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Schaffer([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
if label==3
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Griewank([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
fun.m
function y = fun(x,label)
%函数用于计算粒子适应度值
%x input 输入粒子
%y output 粒子适应度值
if label==1
y=-Rastrigin(x);
elseif label==2
y=-Schaffer(x);
else
y=-Griewank(x);
end
Girewank.m
function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;
Rastrigin.m
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人:
% 编制日期:
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;
Schaffer.m
function y=Schaffer(x)
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;
(2)代码运行结果
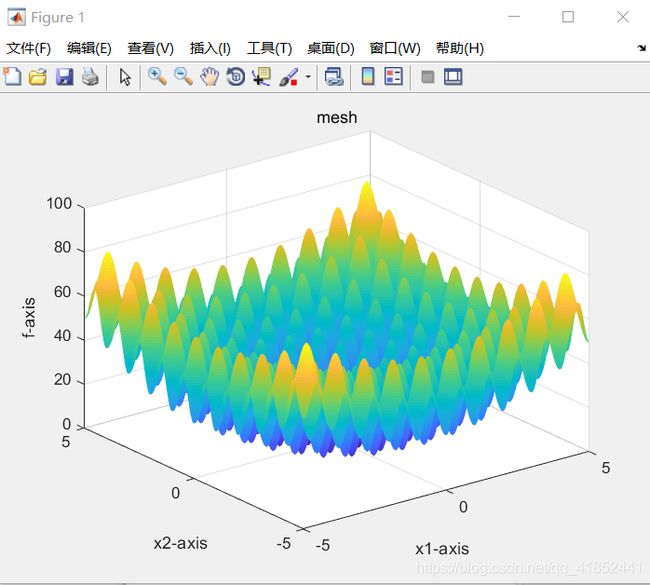
Rastrigin
空间维度:5
种群规模:80
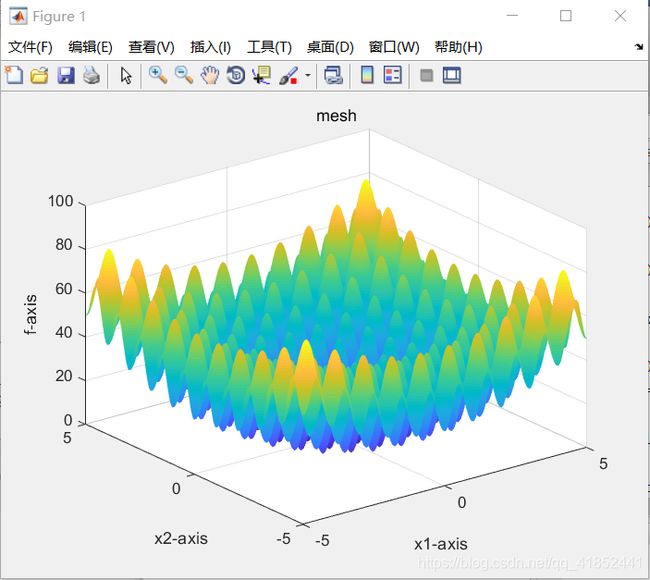
空间维度:10
种群规模:80
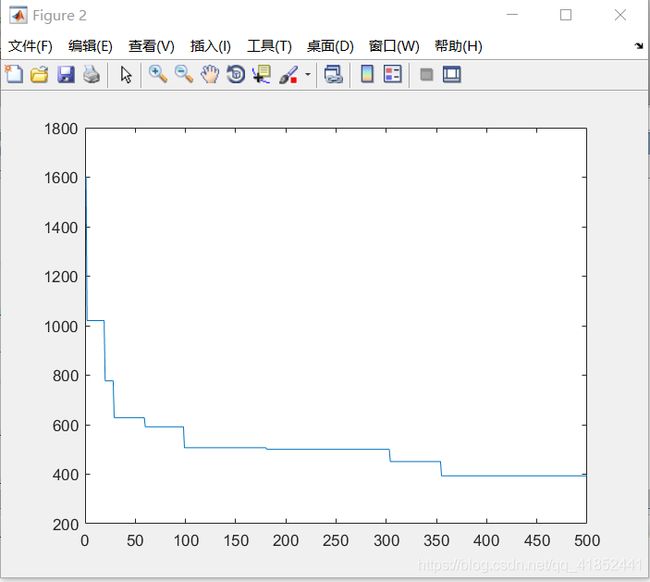
空间维度:5
种群规模:200
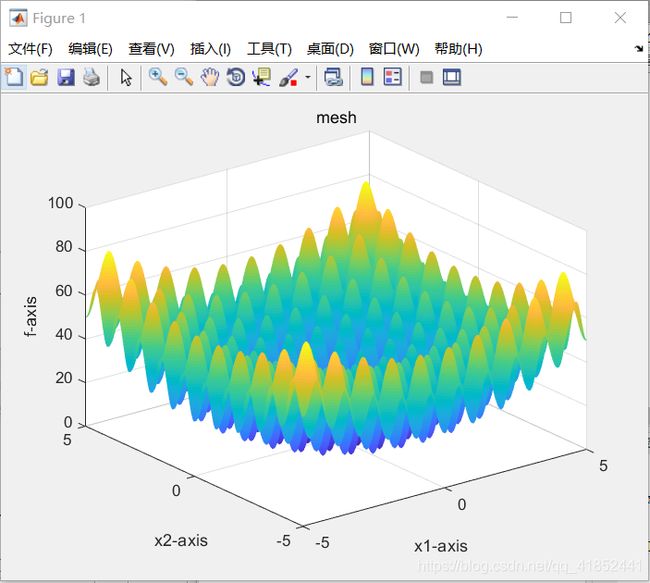
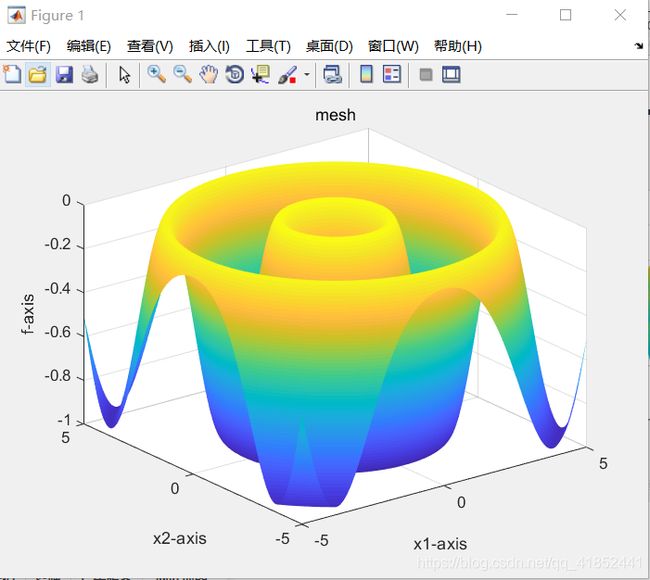
Schaffer
空间维度:5
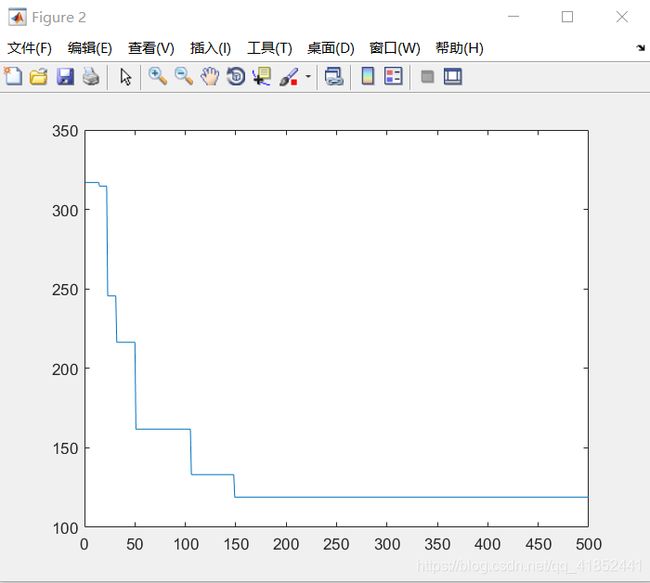
种群规模:80
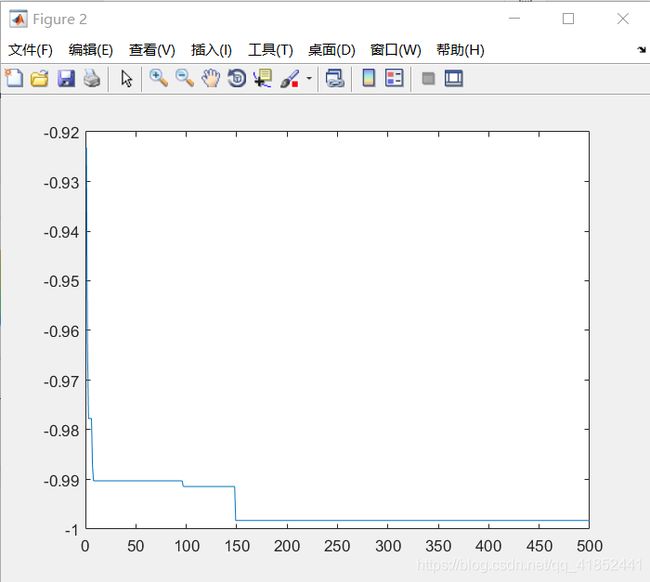
空间维度:10
种群规模:80
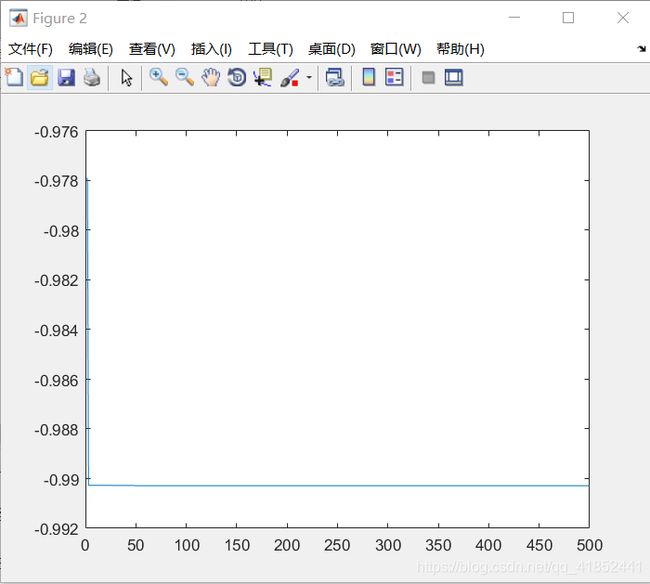
空间维度:5
种群规模:200
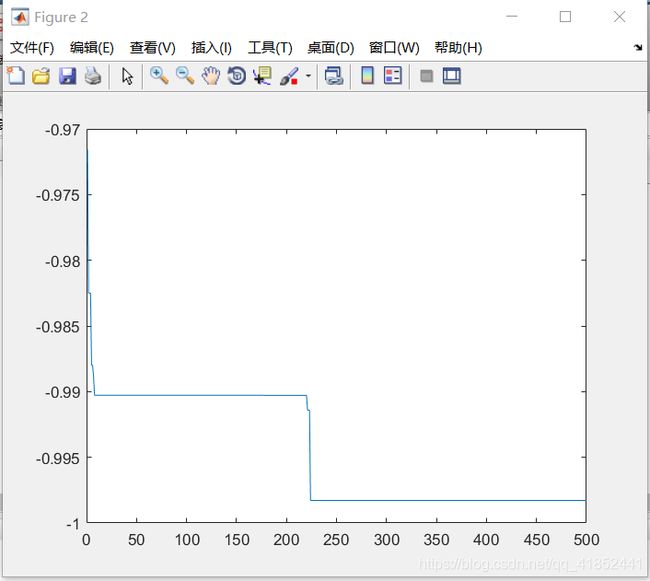
Girewank
空间维度:5
种群规模:80
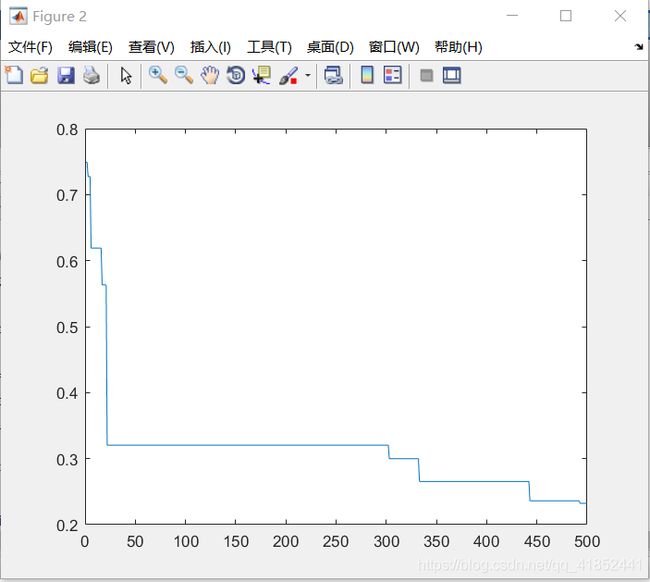
空间维度:10
种群规模:80
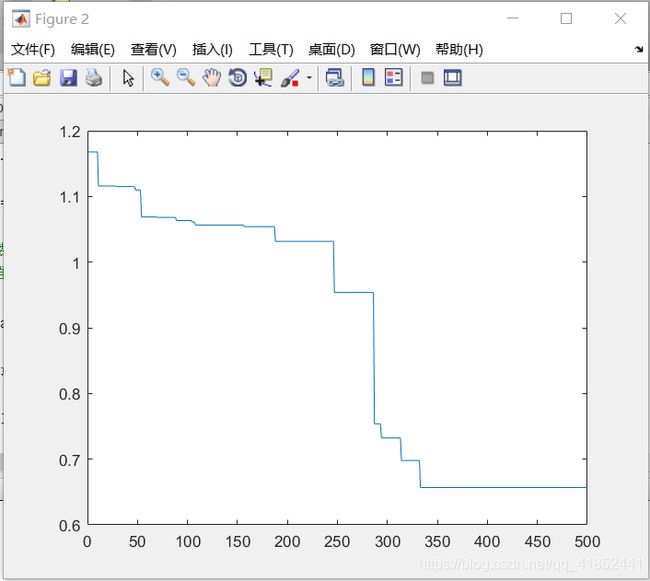
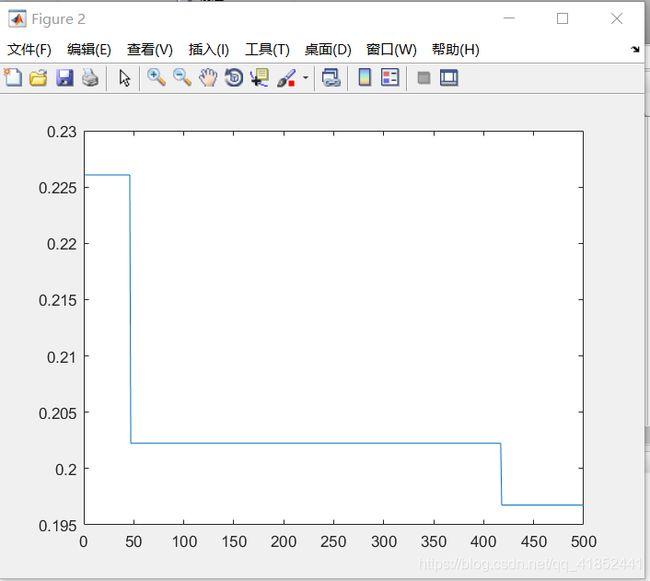
空间维度:5
种群规模:200
5.实验总结
遗传算法的初始种群生成对最终的结果的准确度也有很大的影响,原始的遗传算法初始种群采用随机生成的方式。遗传算法的适应度函数也是决定遗传算法好坏的重要指标,适应度函数的计算主要利用测试数据执行过程中的覆盖来计算适应值。由于遗传算法的整体搜索策略和优化搜索方式在计算时不依赖于梯度信息或其他辅助知识,只需要求解影响搜索方向的目标函数和相应的适应度函数,所以遗传算法提供了一种求解复杂系统问题的通用框架。
6.参考资料
(1)百度百科:遗传算法
(2)csdn资料
(3)csdn博客