ADC前仿真教程
最近做ADC的时候,对ADC的仿真有一个很痛苦的过程,所以特地写一个博客,帮助所有需要仿真ADC的同学,不要走太多弯路吧,本博客是针对差分输入的SARADC
本文主要分为3个部分,首先是介绍ADC仿真需要的数据以及软件,第二部分就是ADC仿真的指标,第三部分就是如何采用数据得到仿真指标。
PART1 电路仿真数据及软件
首先,ADC电路主要存在静态仿真和动态仿真两类仿真,针对两种不同的仿真,我们存在不同的输入信号和不同的数据采样,因此静态仿真和动态仿真是完全不同的两个概念,所以设置的参数不同:
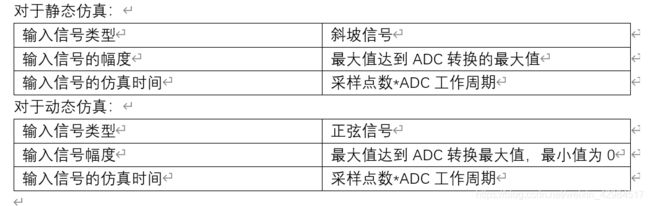
在ADC仿真过程中使用的软件主要有特定的EDA软件,MATLAB,EXCEL
- 静态仿真:
SAR-ADC的静态性能指标主要有积分非线性(INL)和微分非线性(DNL)。积分非线性是指同一采样电压下实际转化的数字码和理想的数字码的差;而差分非线性是指实际曲线下不同采样电压下转化数字码的差。具体的分析如下:假设有一理想的斜坡信号作为差分电压的电压,所以得到的分析波形如下所示:
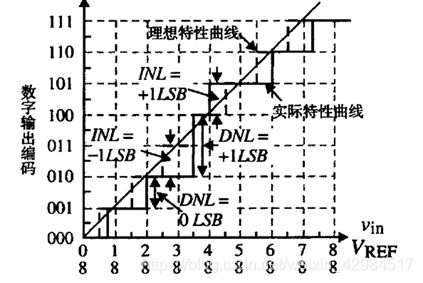
DNL: 从实线阶梯信号中,有数字码H(1),
H(2), H(3),……,H(i);
DNL1 = H(2) – H(1);DNL2
= H(3) – H(2);所以可以总结出规律得到:
则最终的差分非线性表达式为:
INL:从实线阶梯信号和理想阶梯信号中,假设有N个采样点,在第I个采样点的理想数字码为W(I),实际数字码为H(I), 则INL的计算如下:
对于一个优秀的SARADC,输出精度的优势主要取决于INL,DNL的大小,首先INL,DNL的计量单位主要是LSB,对于本电路,LSB可以表示为:
而对于INL, DNL而言假设计算出大于1LSB,则会出现失码的现象,这会导致我们的SARADC输出不准确,从而造成误差。
- 动态仿真
SAR-ADC动态仿真主要性能指标有:信噪比(SNR),信号噪声失真比(SINAD),有效位数(ENOB),总谐波失真(THD),无杂散动态范围(SFDR);对于以上参数指标,主要的定义如下:
SNR:信噪比是输入信号和噪声(不包括任何谐波以及直流) 的功率比,[5]是定义器件内部噪声大小的基本参数。信噪比的计算公式如下:
SINAD:SINAD是输入信号和所有输出信号失真功率(包括谐波成分,不包括直流)比,它测量的是输出信号所有传递函数非线性加上系统所有噪声(量化、抖动和假频)的累积效果。主要的计算公式如下:
ENOB: 表示ADC在转换过程中真正输出有效的位数,此参数与信噪比密切相关,主要计算公式为:
THD: 总谐波失真是输入信号与系统所有谐波的总功率比,它可提供系统对称和非对称非线性产生的失真大小,用以表达其对信号的谐波含量的作用或者影响。
SFDR: 表示器件输入和输出之间的非线性,主要计算公式为如下:
PART 3 ADC仿真流程
静态仿真主要通过采用斜坡信号作为差分输入,此时假设仿真采样1024个点,那么就会相对应ADC转换出1024个无符号二进制数,那么此时通过excel的处理将其转换为十进制数,转换用到的公式主要如下,以11位的为例,
- 使用EXCEL进行转换
输入=后的公式主要为:
BIN2DEC(MID(1,2,选中的二进制数))*512+BIN2DEC(MID(3,11,选中的二进制数))
通过该公式,可以将相应的二进制数转换为十进制数,此时得到的数据则为采样时间对应电压下的ADC转换数字量,重复以上步骤1024次,excel可以批量产生
- 同时,通过公式计算对应电压下理想ADC的转换量
首先,理想的转化量主要是通过以下公式进行转换的,主要表达为:
同样通过这种方法计算可以得到了1024个点的理想数值量
- 使用excel对ADC的理想转换量和实际转换量数据处理
使用excel对ADC的理想转换量和实际转换量进行做差处理,此时得到理想转换量和实际转换量的差值,最后再计算INL,DNL的单位LSB,LSB可以表示为:
LSB = V R E F 2 11 − 1 \frac{V_{REF}}{2^{11} - 1} 211−1VREF
最后通过使用转换量的差和1LSB相除便可以得到1024个结果,取1024个结果的最大值便可以得到INL了
动态仿真:
动态仿真比较复杂,需要借助MATLAB进行FFT分析,得到最终动态分析的参数,首先先差分输入正弦信号进行采样
输入MATLAB的程序在很多网站里面都有资源,那么这里主要对一段MATLAB代码分析一下:
PART1: Sample Number Input
fid=fopen(‘x.txt’,‘r’); %将数据文件存到文本中,其中第一列为取样时间,第二列为取样结果
numpt=2033; %采样的实际码数
fclk=0.005; %采样频率
%MAX1448 - 10-bit data converter
numbit=11; %ADC的位数
fclose(fid);
v1=v1’; %将两列数据变为两行数据存在v1覆盖原来数据
code=v1(:,2); %将采样的数据(即最初x文件的第二列)存到code
PART2: TIME AND FREQUENCY DOMINANT PLOT(时域波形与FFT分析的输出)
Dout=code-(2^numbit-1)/2;
%输出的转换
Doutw=Dout.hanning(numpt);
%输出结果和窗函数相乘得到无失码结果
%Performing
the Fast Fourier Transform
Dout_spect=fft(Doutw);
%Recalculate to dB
Dout_dB=20log10(abs(Dout_spect));
%Display the results in the frequency domain with an FFT plot
figure;
maxdB=max(Dout_dB(1:numpt/2));
%For TTIMD, use the following short routine, normalized to —6.5dB full-scale.
%plot([0:numpt/2-1].*fclk/numpt,Dout_dB(1:numpt/2)-maxdB-6.5);
plot([0:numpt/2-1].*fclk/numpt,Dout_dB(1:numpt/2)-maxdB);
grid on;
title(‘FFTPLOT’);
xlabel(‘ANALOG INPUT FREQUENCY (MHz)’);
ylabel(‘AMPLITUDE(dB)’);
a1=axis;
axis([a1(1) a1(2) -120 a1(4)]);
PART3:
Calculate SNR, SINAD, ENOB,THD and SFDR values
%Find the signal bin number, DC = bin 1
fin=find(Dout_dB(1:numpt/2)==maxdB);
%Span of the input frequency on each side
span=max(round(numpt/200),5);
%Approximate search span for harmonics on each side
spanh=2;
%Determine power spectrum
spectP=(abs(Dout_spect)).(abs(Dout_spect));
%Find DC offset power
Pdc=sum(spectP(1:span));
%Extract overall signal power
Ps=sum(spectP(fin-span:fin+span));
%Vector/matrix to store both frequency and power of signal and harmonics
Fh=[];
%The 1st element in the vector/matrix represents the signal, the next element represents
%the 2nd harmonic, etc.
Ph=[];
%Find harmonic frequencies and power components in the FFT spectrum
for
har_num=1:10
%Input tones greater than fSAMPLE are aliased back into the spectrum
tone=rem((har_num(fin-1)+1)/numpt,1);
if
tone>0.5
%Input tones greater than 0.5fSAMPLE (after aliasing) are reflected
tone=1-tone;
end
Fh=[Fh,tone];
%For this procedure to work, ensure the folded back high order harmonics do not overlap
%with DC or signal or lower order harmonics
har_peak=max(spectP(round(tonenumpt)-spanh:round(tonenumpt)+spanh));
har_bin=find(spectP(round(tonenumpt)-spanh:round(tonenumpt)+spanh)==har_peak);
har_bin=har_bin+round(tonenumpt)-spanh-1;
Ph=[Phsum(spectP(har_bin-1:har_bin+1))];
end
%Determine the total distortion power
Pd=sum(Ph(2:5));
%Determine the noise power
Pn=sum(spectP(1:numpt/2))-Pdc-Ps-Pd;
format;
A=(max(code)-min(code))/2^numbit
AdB=20log10(A)
SINAD=10log10(Ps/(Pn+Pd))
SNR=10log10(Ps/Pn)
ENOB =(SINAD-1.76)/6.02
disp(‘THD is calculated from 2nd through 5th order harmonics’);
THD=10log10(Pd/Ph(1))
SFDR=10log10(Ph(1)/max(Ph(2:10)))
disp(‘Signal& Harmonic Power Components:’);
HD=10log10(Ph(1:10)/Ph(1))
%Distinguish
all harmonics locations within the FFT plot
hold on;
plot(Fh(2)*fclk,0,‘mo’,Fh(3)*fclk,0,‘cx’,Fh(4)*fclk,0,‘r+’,Fh(5)fclk,0,'g’,
Fh(6)*fclk,0,‘bs’,Fh(7)*fclk,0,‘bd’,Fh(8)*fclk,0,‘kv’,Fh(9)*fclk,0,‘y^’);
legend(‘1st’,‘2nd’,‘3rd’,‘4th’,‘5th’,‘6th’,‘7th’,‘8th’,‘9th’);
hold off;
代码并不完整,可以通过上网搜索完整的代码,或者最后在下方留言私聊分享,通过以上
步骤,可以得到我们所需的所有仿真数据了。