卡尔曼滤波：究竟滤了谁？

在SLAM系统中，后端优化部分有两大流派：一派是基于马尔科夫性假设的滤波器方法，认为当前时刻的状态只与上一时刻的状态有关；另一派是非线性优化方法，认为当前时刻状态应该结合之前所有时刻的状态一起考虑。

如果采用滤波器方法，那一定会听到一个如雷贯耳的名字——卡尔曼滤波(Kalman Filtering)。我听到过这个名字已经很久了，可是一直没有花时间弄懂究竟是什么东西，最近看了一些资料，就来总结一下，看看卡尔曼大佬究竟滤了谁？

1 什么是滤波

在了解卡尔曼滤波之前，本科就学过一些滤波的方法，也就是从混合在一起的信号里提取出所需要的信号，就好比吃辣子鸡丁时只把鸡丁挑出来啃光，而辣椒被你抛弃掉了。

例如，在模拟电路中，我们利用低通滤波的方法，将信号中掺杂的一些频率较高的噪声滤除掉，从而提取有效的较低频信号。同样地，根据不同需要，还有高通滤波、带通滤波和带阻滤波。

再比如，在图像处理中，如果存在椒盐噪声（不能吃的！是在图像中随机出现的黑白点），我们会选择用中值滤波，将$n\times n$个像素值的中值取出来以代替中心点的值，这样就能滤除椒盐噪声。

但是，卡尔曼滤波和上述说的这些滤波略显不同，它并没有很直观地从一些信号或者数据里面提取某些信号或数据，而是在有干扰的条件下，通过数据的结合得到相对更准确的估计数据。

卡尔曼滤波全程只关注两个东西，一个是估计的最佳值，另一个是该值的不确定性（此处联想一下高斯分布的两个参数）。

打个比方，假设你蒙着眼睛在屋子里走，要从客厅走到卧室，你可以通过数步数来预测你当前所在的位置，但是因为你每次迈步的幅度和方向不是精准的，所以你每多走一步所估计位置的不确定性就会越来越大，最后有可能走到浴室去了。

如果利用卡尔曼滤波，那么你对自己每一步的位置估计就会准确很多，具体怎么做呢？卖个关子，后面再讲，先解释一下什么是状态估计。

2 状态估计

在SLAM中，运用卡尔曼滤波是为了状态估计，那什么才是需要估计的状态呢？

状态可以看作是机器人或者环境中可能会对未来产生某些变化的因素，比如说机器人的位姿$\mathbf{R}$和$\mathbf{t}$、机器人的运动速度$\mathbf{v}$(这个在纯视觉SLAM中是没有的)、环境中的路标点$\mathbf{l}$等等，不同的SLAM系统拥有不同的状态。

我们假设${\mathbf{x}}_k$为机器人的状态，在SLAM的整个过程中，我们能获取到两种数据：控制数据和测量数据。

• 控制数据是机器人记录自身运动的传感器获取的数据，比如IMU中的陀螺仪可以测量角速度、加速度计可以测量运动的加速度。

• 测量数据则是机器人记录环境信息的传感器获取的数据，比如相机可以将环境转化为二维的图像像素、激光雷达捕捉环境中的信息生成点云。

假设控制数据为${\mathbf{u}}_k$，运动噪声为${\mathbf{\epsilon }}_k$，那么机器人的运动可以用一个运动方程来表达，因为假设了马尔科夫性，所以当前时刻状态只与上一时刻有关，它表示从k-1时刻到k时刻机器人状态发生了怎样的变化。
$${\mathbf{x}}_k=f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{\epsilon }}_k$$

假设测量数据为${\mathbf{z}}_k$，测量噪声为${\mathbf{\delta }}_k$，那么机器人的测量可以用一个观测方程来表达，它表示在k时刻所在的位置观测到路标点产生测量数据。
$${\mathbf{z}}_k=h\left({\mathbf{x}}_k\right)+{\mathbf{\delta }}_k$$

那么，状态估计其实就是用过去的数据来估计当前的状态。由于状态不是直接得到的，而且方程还受到噪声的影响，因此状态其实是符合某种概率分布的随机变量，而状态估计实际上是估计当前的状态分布。

我们用置信度$bel({\mathbf{x}}_k)$来表示当前时刻的状态分布，它是以控制数据和测量数据为条件的后验概率，即
$$bel({\mathbf{x}}_k)=p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k},{\mathbf{u}}_{1:k}\right)$$

而在获得当前时刻测量数据之前的状态分布可以用$\overline{bel}\left({\mathbf{x}}_k\right)$来表示，它表示的后验概率为
$$\overline{bel}({\mathbf{x}}_k)=p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)$$

同时，如果用概率来表达运动过程的话，则是$p\left({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)$，这表示了从k-1时刻到k时刻机器人的状态转移概率。而用概率来表达观测过程，则是$p\left({\mathbf{z}}_k|{\mathbf{x}}_k\right)$，表示第k时刻机器人的测量概率。

所以，如下图所示，每一时刻的状态${\mathbf{x}}_k$只与前一时刻的状态${\mathbf{x}}_{k-1}$和当前时刻的控制${\mathbf{u}}_k$有关，而每一时刻的测量${\mathbf{z}}_k$只与当前时刻的状态${\mathbf{x}}_k$有关。这就是一个隐马尔可夫模型，状态不能直接得到，但是可以通过测量观察到。

3 贝叶斯滤波

有了状态分布的表达方式，还有运动方程和观测方法的概率表示，接下来就可以名正言顺地献上著名的贝叶斯公式了(前方多式警告！)
$$p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k},{\mathbf{u}}_{1:k}\right)=\frac{p\left({\mathbf{z}}_k|{\mathbf{x}}_k,{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)}{p\left({\mathbf{z}}_k|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)}$$

因为分母和状态没有半毛钱关系，因此可以用一个比例因子$\eta$来表示，即
$$p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k},{\mathbf{u}}_{1:k}\right)=\eta p\left({\mathbf{z}}_k|{\mathbf{x}}_k,{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)$$

根据前面说到的置信度和观测方程的概率表示(测量概率)，该式还可以表示为
$$bel({\mathbf{x}}_k)=\eta p\left({\mathbf{z}}_k|{\mathbf{x}}_k\right)\overline{bel}({\mathbf{x}}_k)$$

对于$\overline{bel}({\mathbf{x}}_k)$，用边际概率公式$p(x)=\int p(x|y)p(y)dy$可以得到
$$\begin{array}{rl}\overline{bel}\left({\mathbf{x}}_k\right)& =p\left({\mathbf{x}}_k|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)\\ & =\int p\left({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)p\left({\mathbf{x}}_{k-1}|{\mathbf{z}}_{1:k-1},{\mathbf{u}}_{1:k}\right)d{\mathbf{x}}_{k-1}\end{array}$$

根据前一时刻的置信度和运动方程的概率表示(状态转移概率)，同时状态${\mathbf{x}}_{k-1}$与${\mathbf{u}}_k$不相关，因此上式化简得
$$\overline{bel}\left({\mathbf{x}}_k\right)=\int p\left({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)bel({\mathbf{x}}_{k-1})d{\mathbf{x}}_{k-1}$$

可以看出，这是一个递归的过程，每一时刻的状态分布根据前一时刻的状态分布计算得到，一直追溯到初始状态${\mathbf{x}}_0$。

于是，我们就可以得到贝叶斯滤波算法了。

Algorithm Bayes_filter($bel({\mathbf{x}}_{k-1}),{\mathbf{u}}_k,{\mathbf{z}}_k$):
    for all ${\mathbf{x}}_k$ do
        $\overline{bel}\left({\mathbf{x}}_k\right)=\int p\left({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)bel({\mathbf{x}}_{k-1})d{\mathbf{x}}_{k-1}$
        $bel({\mathbf{x}}_k)=\eta p\left({\mathbf{z}}_k|{\mathbf{x}}_k\right)\overline{bel}({\mathbf{x}}_k)$
    end for
    return $bel({\mathbf{x}}_k)$

首先，根据上一时刻的状态分布，机器人经过运动方程的状态转移概率进行预测，得到综合测量数据前的当前时刻状态分布。然后，通过观测方程将测量数据考虑进来，再对状态分布进行调整更新，得到最当前时刻最终的状态估计。

因此，只要知道初始状态分布$bel({\mathbf{x}}_0)$、运动方程的状态转移概率$p\left({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)$和观测方程的测量概率$p\left({\mathbf{z}}_k|{\mathbf{x}}_k\right)$，贝叶斯滤波就可以滤起来了！

4 卡尔曼滤波

呼！有了前面一堆的铺垫之后，终于迎来了重头戏卡尔曼滤波。在这里先附上大牛的照片以表敬意，要知道当年设计出的卡尔曼滤波器可是要上天的！

其实理解了贝叶斯滤波之后，卡尔曼滤波也不难明白。因为卡尔曼滤波是一种特殊的贝叶斯滤波，它假定系统是线性高斯的，也就是说卡尔曼滤波=贝叶斯滤波$\cap$线性高斯系统。

这是什么意思呢？还记得前面提及的运动方程吗，它在线性系统中的表达为
$$\begin{array}{rl}{\mathbf{x}}_k& =f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k\right)+{\mathbf{\epsilon }}_k\\ & ={\mathbf{A}}_k{\mathbf{x}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{\epsilon }}_k\end{array}$$

而观测方程在线性系统中的表达为
$$\begin{array}{rl}{\mathbf{z}}_k& =h\left({\mathbf{x}}_k\right)+{\mathbf{\delta }}_k\\ & ={\mathbf{C}}_k{\mathbf{x}}_k+{\mathbf{\delta }}_k\end{array}$$

与此同时，运动噪声${\mathbf{\epsilon }}_k$和测量噪声${\mathbf{\delta }}_k$都是随机高斯噪声，即
$${\mathbf{\epsilon }}_k\sim N\left(0,{\mathbf{R}}_k\right),{\mathbf{\delta }}_k\sim N\left(0,{\mathbf{Q}}_k\right)$$

因此，运动方程的状态转移概率和观测方程的测量概率都相应地满足高斯分布
$$p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{u}}_k)\sim N\left({\mathbf{A}}_k{\mathbf{x}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k,{\mathbf{R}}_k\right)$$

$$p\left({\mathbf{z}}_k|{\mathbf{x}}_k\right)\sim N\left({\mathbf{C}}_k{\mathbf{x}}_k,{\mathbf{Q}}_k\right)$$

由于初始状态分布也要满足高斯分布，而且高斯分布相乘依然为高斯分布，所以在整个递归的滤波过程中，状态估计始终满足高斯分布，Amazing！

还记得贝叶斯滤波一直维护更新的是状态分布$\overline{bel}\left({\mathbf{x}}_k\right)$和$bel\left({\mathbf{x}}_k\right)$吗？在卡尔曼滤波中也是如此，只不过因为卡尔曼滤波应用在线性高斯系统中，状态分布都满足高斯分布，因此卡尔曼滤波关心的是均值${\bar{\mathbf{\mu }}}_k$、${\mathbf{\mu }}_k$和方差${\bar{\mathbf{\Sigma }}}_k$、${\mathbf{\Sigma }}_k$。

因此，卡尔曼滤波算法过程为

Algorithm Kalman_filter(${\mathbf{\mu }}_{k-1},{\mathbf{\Sigma }}_{k-1},{\mathbf{u}}_k,{\mathbf{z}}_k$):
    for all ${\mathbf{x}}_k$do
        ${\bar{\mathbf{\mu }}}_k={\mathbf{A}}_k{\mathbf{\mu }}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k$
        ${\bar{\mathbf{\Sigma }}}_k={\mathbf{A}}_k{\Sigma }_{k-1}{\mathbf{A}}_k^T+R_k$
 
        ${\mathbf{K}}_k={\bar{\mathbf{\Sigma }}}_k{\mathbf{C}}_k^T{\left({\mathbf{C}}_k{\bar{\mathbf{\Sigma }}}_k{\mathbf{C}}_k^T+{\mathbf{Q}}_k\right)}^{-1}$
        ${\mathbf{\mu }}_k={\bar{\mathbf{\mu }}}_k+{\mathbf{K}}_k\left({\mathbf{z}}_k-{\mathbf{C}}_k{\bar{\mathbf{\mu }}}_k\right)$
        ${\mathbf{\Sigma }}_k=\left(\mathbf{I}-{\mathbf{K}}_k{\mathbf{C}}_k\right){\bar{\mathbf{\Sigma }}}_k$
    end for
    return ${\mathbf{\mu }}_k$, ${\mathbf{\Sigma }}_k$

可以看到，卡尔曼滤波和贝叶斯滤波一样也是分为两个步骤，先是根据前一时刻状态分布的均值和方差还有控制数据预测当前时刻的均值和方差，然后再根据测量数据调整更新当前时刻最终的均值和方差，只不过卡尔曼滤波多了一个求卡尔曼增益${\mathbf{K}}_k$的过程。

卡尔曼滤波和贝叶斯滤波的对比如下图

由于篇幅原因，就不进行公式推导了。如果觉得不够直观，那么就举个栗子用图来解释一下。

5 举个栗子

下面就用图来解释一下卡尔曼滤波，能有个更直观的感受。

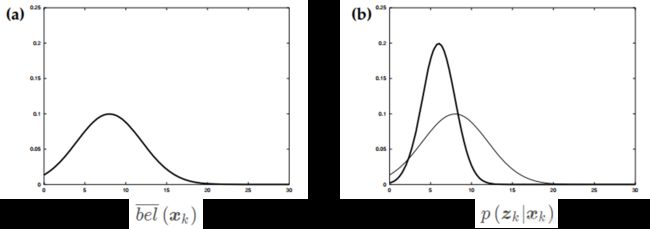
首先通过上一时刻的状态预测得到当前时刻的状态分布(图a)，然后通过传感器得到测量数据(图b加粗)。

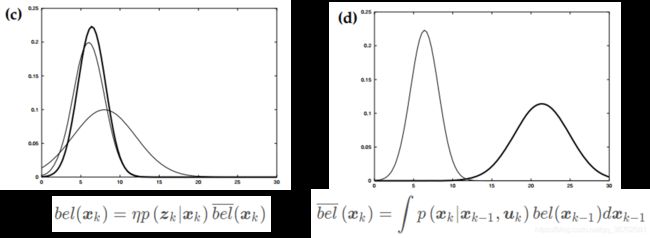
结合测量数据调整更新，得到当前时刻最终的状态分布(图c加粗)。然后通过控制数据，接着预测下一时刻的状态分布(图d加粗)。

获取下一时刻的测量数据之后(图e加粗)，综合得到下一时刻估计的状态分布(图f加粗)。

到这，你知道卡尔曼滤波究竟滤了谁吗？在我看来，卡尔曼滤波可以看作是，通过测量数据将仅由控制数据进行状态估计而带来不断提高的噪声(不确定性)滤除掉。同时，它更像是一种数据(传感器)融合的方法。

还记得文章前面让你蒙着眼在屋子里走吗？学了卡尔曼滤波之后应该知道怎么做能让你更准确地知道当前位置了吧？很简单，那就是睁开眼走路！

眼睛看到室内环境就相当于测量数据，综合眼睛看到的景象就会让你对自己所在的位置判断更准确啦。当然，如果你的鼻子够灵，可以通过气味判断，或者有顺风耳可以听到浴室滴水从而避免掉坑也是可以的！

我在知乎上也看到知友Kent Zeng对卡尔曼滤波有更入木三分的见解：

假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？
—— 取平均。
再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？
——加权平均。
怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，（此处省略若干数学公式），你可以得到一个“最优”的权重。
接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型。模型可以帮你算出一个值，但也不是那么准。怎么办？
—— 把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均。
OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。问题是x(k)是多少呢？答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个、对x在k时刻的最佳估计值。
于是迭代也有了。

想把卡尔曼滤波吃透不容易，如果打算用滤波作为SLAM的后端部分，那还有大堆卡尔曼滤波的变体在扑向你~

看完卡尔曼滤波后，耳边不禁响起一句:

“SLAM是一道光，滤到你发慌”！

最后，祝大家滤波开心！

参考资料：

1.《视觉SLAM十四讲：从理论到实践 第2版》高翔等人著

2.《概率机器人》Sebastian Thrun等人著

3.《策略不给力？来一发卡尔曼滤波》知乎Fitz Hoo文章

4.《如何通俗并尽可能详细地解释卡尔曼滤波？》知乎Kent Zeng回答

5.《图说卡尔曼滤波，一份通俗易懂的教程》知乎论智文章