L2-Net 论文详解

L2-Net

本文提供了相应的代码，是基于 matconvnet，论文的思路相对来说比较简单，可以使用 pytorch 或者 tersorflow 等框架复现。

主要思路

之前有 SIFT 等手工设计的 patch 特征，这里提出的 L2-Net 的方法，利用 CNN 方法在 Euclidean 空间学习 patch 特征。本文主要的工作包括：

1. 提出递进的采样策略，可以保证网络在很少的 epochs 就可以访问到数十亿的训练样本。
2. 重点关注 patch 特征之间的相对距离，就是匹配上的 patch pair 距离比未匹配上的 patch pair 距离更近。
3. 对学习过程中间的 feature maps 进行额外的监督。
4. 同时会考虑特征的 compactness（紧凑程度）。

利用网络输出特征向量后，用 $L_2$ 距离当做在 Euclidean 空间的相似程度。而且这个和传统特征是完全一致的，这样在很多方法里面可以直接用 L2-Net 的特征进行替换。

本文的主要目的是输出 patch 对应的 128d 的特征向量，而不去关注 metric 的学习，有了特征向量后直接利用 $L_2$ 来度量相似度，简单来说就是在特征空间里面进行 nearest neighbor search (NNS) 查找最近的 patch 作为匹配结果。本文的关注的只要 matching pairs 都互为最近邻即可，而实际距离的大小和量级不需要太过关心，也就是只关注相对距离。这算是本文的核心思路吧，后面 training batch 构建以及网络结构和 loss 涉及都和这个思路相关。

基本流程

网络架构

本文 L2-Net 整体的网络架构如下图所示：

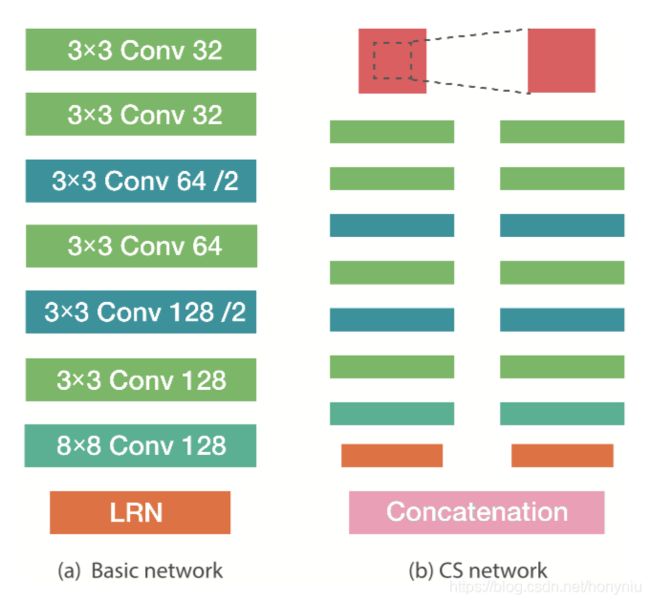
左图是基本架构，其中利用的是全卷积网络，同时 feature map 降维是利用卷积层的 stride 设置为 2 实现的。每个卷积后面都跟着一个 BN 层，但是该 BN 层的参数不会在训练过程中去更新（w和b固定为1和0）。网络最后使用 Local Response Normalization (LRN) 层输出一个单位特征向量。

其中输入是 $32\times 32$ 大小的 patch，输出是 128d 的特征向量。

同时参考 DeepPatchMatch 和 DeepCompare ，实现了 central-surround (CS) L2-Net，如上面右图，左边分支输入是原始的 patch，右边分支输入是在原始 patch 基础上中间 crop 然后 resize 到同样大小，然后经过同样的网络，把最后特征向量拼接在一起，得到最后的特征向量。

CS 这种操作的好处是为了处理特征 scale 不变性的问题，但是有个疑问就是 CNN 框架是也可以处理这种 scale 情况的，估计是效果不太好。

训练数据和预处理

本文训练数据使用的是 Brown 和 HPatches，是在不同的场景下采集的。但是组织方式一致，如下：

1. 每个 patch 都有独一无二的 3D 点的 index 属性，如果 patches 的该属性一致，则认为具有匹配关系；
2. 当然对于每个 3D 点，至少有两个相关的匹配的 patches；

其中 Brown 数据集包含 Yosemite, Notredame, and Liberty 三个子集，通常情况都是一个子集用来 train，其他两个用于 test。

其中 HPatches 数据集被分成 train-hard (easy) -viewpoint 和 train-hard (easy) -illum 四个子集，表示不同的 view 和 光线的变化程度。HPatches 只当做 train 数据集。

其中 Brown 数据包含 500K (1.5M) 个 3D 点，HPatches 包含 190K (1.2M)个 3D 点。

实际训练时每个 patch 直接 resize 到 $32\times 32$，同时对每个 pixel 做 mean 和 scale 的 norm 操作。

递进采样策略

首先在 patch matching 的问题上，负样本数量要远远高于正样本，一对匹配的 patch pair，除了互相匹配之外，其中每个 patch 和数据库中的除这两个之外的 patch 都可以组成负样本，这就导致很难在训练过程中遍历所有的负样本，所以需要一个好的采样策略。

之前的工作都是采样相同数目的正负样本，本文的递进采样策略则会采样更多的负样本。具体采样过程如下：

在训练数据集中有个 $P$ 个 3D 点，首先选择其中的 $p_1$ 个点，按照顺序遍历所有的 3D 点，然后从余下的 $P-p1$ 个 3D 点随机选取 $p_2$ 个点，$p_2$ 3D 点的选取增加了数据的 random， $p_1+p_2$ 当做每个 training batch 选择的 3D 点。

然后为了得到最终的 training batch，对 $p=p_1+p_2$ 中的每个点，随机选取一对 matching patches（每个 3D 点可能对应更多的 patches），所以最终的 training batch为：

$$\mathbf{X}={\left\{{\mathbf{x}}_1^1,{\mathbf{x}}_1^2,\cdots ,{\mathbf{x}}_i^1,{\mathbf{x}}_i^2,\cdots ,{\mathbf{x}}_p^1,{\mathbf{x}}_p^2\right\}}_{32\times 32\times 2p}$$

其中下标是 3D 点的 $index$，上标 2D patch 的 $index$，${\mathbf{x}}_i^1$ 和 ${\mathbf{x}}_i^2$ 表示 3D 点的对应的一对匹配的 patch pair。这 $\mathbf{X}$ 是 L2-Net 的输入，输出是：

$$\mathbf{Y}={\left[{\mathbf{y}}_1^1,{\mathbf{y}}_1^2,\cdots ,{\mathbf{y}}_i^1,{\mathbf{y}}_i^2,\cdots ,{\mathbf{y}}_p^1,{\mathbf{y}}_p^2\right]}_{q\times 2p}$$

其中 $\mathbf{Y}$ 为网络经过 LRN 层得到的结果，$q=128$ 为输出的特征向量维度。

定义距离矩阵为：

$$\begin{gathered} \mathbf{D}={\left[d_{ij}\right]}_{p\times p} \\ 其中d_{ij}={\Vert {\mathbf{y}}_i^2-{\mathbf{y}}_j^1\Vert }_2\left(\Vert {\Vert }_2\text{ is }{L}_2\text{ norm }\right) \end{gathered}$$

这个 $\mathbf{D}$ 可以直接用一个矩阵乘法计算：

$$\begin{gathered} \mathbf{D}=\sqrt{2\left(1-{\mathbf{Y}}_1^{\mathbf{T}}{\mathbf{Y}}_2\right)} \\ 其中{\mathbf{Y}}_{\mathbf{s}}={\left[{\mathbf{y}}_1^s,\cdots ,{\mathbf{y}}_i^s,\cdots ,{\mathbf{y}}_p^s\right]}_{q\times p},(s=1,2) \end{gathered}$$

其中 $\mathbf{D}$ 包含 $p^2$ 个 patch pairs 的距离，其中 $p$ 个是正样本（矩阵对角线元素），$p^2-p$ 个负样本（矩阵除对角线之外元素）。

根据上面的叙述，假设有 $160K$ 的 3D 点，设置 $p=128$，那么每个 training epoch 包含 $2500$ 个上面的 traning batches，大概 $40\mathrm{M}\left(128^2\times 2500\right)$ patch pair（这里虽然总共training batch只有 $128\times 2$ 个 patches，但是参入计算的 pairs 是 $128^2$）。

而且总共需要训练 40 个 epoches，这样将近 16 亿个 pairs 需要计算，除了大量的负样本外，正样本数目大概为 $12.8\mathrm{M}(128\times 2500\times 40)$。

这里有个问题是每个 training batch 包含 $128\times 2$ 个patches，每个 patch 除了与自身和匹配的 patch 外，其实和其他所有的 patches 都能计算一个距离当做负样本的，但本文只选择了匹配 patch pair 中的一个来计算负样本。如果按照全部计算的话，那么 $\mathbf{D}$ 公式 ${\mathbf{Y}}_1^{\mathrm{T}}{\mathbf{Y}}_2$ 就变成了 ${\mathbf{Y}}^{\mathbf{T}}\mathbf{Y}$，这样结果中对角线值都为 0，表示 patch 自身的距离，而其中正样本和负样本都在非对角线元素上，这样不仅仅是计算量增加，更多的是带来不好去计算梯度，增加了计算的复杂度。而且本文也测试过使用该方法，但是性能并没有太提高。

Loss 函数

根据上面的递进采用策略，loss 函数包含三个目标函数：

1. 利用相对距离区分匹配上和未匹配上的 patch pairs；
2. 考虑最后输出特征向量的 compactness，也就是特征向量的各个维度尽可能不相关；
3. 学习过程中间的 feature maps 进行额外的监督，可以得到更好的性能；

描述符相似度的误差项

loss error 基于相对距离，nearest neighbor 是哪个匹配上的 patch pairs。在 $\mathbf{D}$ 里面就是：

$$\underset{(i,j)\in [1,p]}{\min }\left\{d_{ik},d_{kj}\right\}=d_{kk}$$

行列拆开来看就是：

$$\{\begin{array}{rl}\underset{i\in [1,p]}{\min }\left\{d_{ik}\right\}& =d_{kk}\\ \underset{j\in [1,p]}{\min }\left\{d_{kj}\right\}& =d_{kk}\end{array}$$

这就很好理解了，也就是 $k$ 行或者 $k$ 列最小的那个 distance 都必须是对角线上元素 $d_{kk}$，也就是匹配上的那个 patch pair 的 distance。

为了实现上的简单，行列分开计算，如下：

$$\begin{gathered} {\mathbf{S}}^c={\left[s_{ij}^c\right]}_{p\times p}列相似度矩阵 \\ 其中s_{ij}^c=\exp \left(2-d_{ij}\right)/\sum _m\exp \left(2-d_{mj}\right) \\ {\mathbf{S}}^r={\left[s_{ij}^r\right]}_{p\times p}行相似度矩阵 \\ 其中s_{ij}^r=\exp \left(2-d_{ij}\right)/\sum _n\exp \left(2-d_{jn}\right) \end{gathered}$$

其中 $2$ 是两个单位向量的最大距离。

其中 ${\mathcal{S}}_{ij}^c$ 可以被认为 $y_i^2$ 匹配上 $y_j^2$ 的可能性，同理 ${\mathcal{S}}_{ij}^r$ 可以被认为 $y_i^1$ 匹配上 $y_j^2$ 的可能性。也就是对 $\mathbf{D}$ 每一行和每一列当做一个分类任务，分别求 softmax 得到 ${\mathbf{S}}^c$ 和 ${\mathbf{S}}^r$，最终 loss error 值为（类似 softmax loss，$-log$）：

$$E_1=-\frac{1}{2}\left(\sum _i\log s_{ii}^c+\sum _i\log s_{ii}^r\right)$$

描述符 compactness 的误差项

实验中发现 overfitting 的程度和特征描述符各维度之间的关联度是正相关的，本文提出一种计算描述符 compactness （即各个维度直接关联度）的误差项来防止过拟合。描述符 compactness 表示各个维度之间信息没有冗余，而每个维度可以表示ge那个可能多的信息，这样和冗余情况相比更少的维度可以达到相同的性能，另一角度看同样的维度下描述符 compactness 程度越高，就可以表示更多的信息，一定层度可以减少 overfitting。

compactness 在之前的一些二进制描述符工作中经常被使用，如 BOLD 和 RFD，通常是采用暴力的查找选择那些变化比较大的 bits，对于描述符的某个维度来说，在大量描述符数据上如果该维度变化越大，一般就是指方差越大，可以说明该维度信息有效性越高。

本文也采用了该思想，而且为了使该过程可进行反向传播，尝试使用相关系数矩阵（correlation matrix），具体公式为：

$$\begin{gathered} {\mathbf{R}}_s={\left[r_{ij}^s\right]}_{q\times q} \\ {r}_{ij}^s=\frac{{\left({\mathbf{b}}_i^s-\overline{b_i^s}\right)}^T\left({\mathbf{b}}_j^s-\overline{b_j^s}\right)}{\sqrt{{\left({\mathbf{b}}_i^s-\overline{b_i^s}\right)}^T\left({\mathbf{b}}_i^s-\overline{b_i^s}\right)}\sqrt{{\left({\mathbf{b}}_j^s-\overline{b_j^s}\right)}^T\left({\mathbf{b}}_j-\overline{b_j^s}\right)}} \\ {\mathbf{Y}}_{\mathbf{s}}^{\mathbf{T}}\text{ as }\left[{\mathbf{b}}_1^s,\cdots ,{\mathbf{b}}_i^s,\cdots ,{\mathbf{b}}_q^s\right]其中{\mathbf{b}}_i^s是行向量，代表p个patch的描述符的第i个维度集合 \end{gathered}$$

其中 $\overline{b_j^s}$ 是 ${\mathbf{Y}}_{\mathbf{s}}$ 第 $i$ 行的均值。

优化目标是希望该相关系数矩阵 ${\mathbf{R}}_s$ 的非对角线元素之都为 0，简化得到误差项为：

$$E_2=\frac{1}{2}\left(\sum _{i̸=j}{\left(r_{ij}^1\right)}^2+\sum _{i̸=j}{\left(r_{ij}^2\right)}^2\right)$$

实际中这个 $s=1$ 和 $s=2$ 是同时输入，在计算时做了区分。

$E_2$ 是在 LRN 层之间计算的，主要是前面正好是 BN 层，做了 mean 和 scale 处理，所以最好简化为：

$${\mathbf{R}}_s={\mathbf{Y}}_s{\mathbf{Y}}_s^{\mathbf{T}}/q$$

中间 feature maps 误差项

本文对学习过程中间的 feature maps 进行额外的监督，进一步提供性能。该误差项思路和 $E_1$ 完全类似，就是匹配上 patch pairs 的中间 feature maps 尽可能相似，而非匹配的则是尽可能不同。

这里定义第 $k$ 层输出的 feature maps 为：

$$\begin{gathered} \mathbf{F}={\left[{\mathbf{f}}_1^1,{\mathbf{f}}_1^2,\cdots ,{\mathbf{f}}_i^1,{\mathbf{f}}_i^2,\cdots ,{\mathbf{f}}_p^1,{\mathbf{f}}_p^2\right]}_{(wh)\times 2p} \\ 其中{\mathbf{f}}_i^s是向量化的featuremap，长度为wh \end{gathered}$$

和上面描述符 distance 计算很类似，中间 feature maps 的内积矩阵为：

$$\begin{gathered} \mathbf{G}={\left[g_{ij}\right]}_{p\times p} \\ \mathbf{G}={\left({\mathbf{F}}_1\right)}^{\mathbf{T}}{\mathbf{F}}_2 \\ {\mathbf{F}}_s={\left[{\mathbf{f}}_1^s,\cdots ,{\mathbf{f}}_i^s,\cdots ,{\mathbf{f}}_p^s\right]}_{(wh)\times p}(s=1,2) \end{gathered}$$

和上面描述符相似度的误差项计算也很类似，中间 feature maps 误差项为：

$$\{\begin{array}{rl}\underset{i\in [1,p]}{\min }\left\{g_{ik}\right\}& =g_{kk}\\ \underset{i\in [1,p]}{\min }\left\{g_{kj}\right\}& =g_{kk}\end{array}$$

同样行列分开计同样如下：

$$\begin{gathered} {\mathbf{V}}^c=\left[v_{ij}^c\right]p\times p列相似度矩阵 \\ {v}_{ij}^c=\exp \left(g_{ij}\right)/\sum _m\exp \left(g_{mj}\right) \\ {\mathbf{V}}^r={\left[v_{ij}^r\right]}_{p\times p}行相似度矩阵 \\ {v}_{ij}^r=\exp \left(g_{ij}\right)/\sum _n\exp \left(g_{jn}\right) \end{gathered}$$

最终 loss error 值为（类似 softmax loss，$-log$）：

$$E_3=-\frac{1}{2}\left(\sum _i\log v_{ii}^c+\sum _i\log v_{ii}^r\right)$$

这里提出的方法为 Discriminative Intermediate Feature maps (DIF)，实验证明 DIF 应用在 normalized feature maps 后更好。本文把 DIF 放在 BN 层后面，具体的是放在 first 和 last 的 BN 层后面。主要是 first BN 层之间跟着输入数据，last BN 层后面直接跟着输出，这样 feature maps 的顺序相对固定。 不太理解这个顺序影响。

最终的误差项

$E_1$ 跟在最后的输出后面，$E_2$ 跟在 last BN 层后面，$E_3$ 跟在first 和 last 的 BN 层后面。最终的误差项为：

$$E=E_1+E_2+E_3$$

Training

L2-Net 没有预训练，直接从 scratch 开始训练。CS L2-Net 则是用训练好的 L2-Net 去初始化，两个分支都进行初始化，不过在训练时左边分支参数固定不进行 finetune，只是右边分支参数更新进行 finetune。

设置 $p1=p2=q/2=64$，其他超参和具体训练过过程参考论文。

实验

Brown

按照 Brown 数据集提出的方法进行评价，大概 $100K$ pairs，然后比较 false positive rate at 95% recall。结果如下图所示：

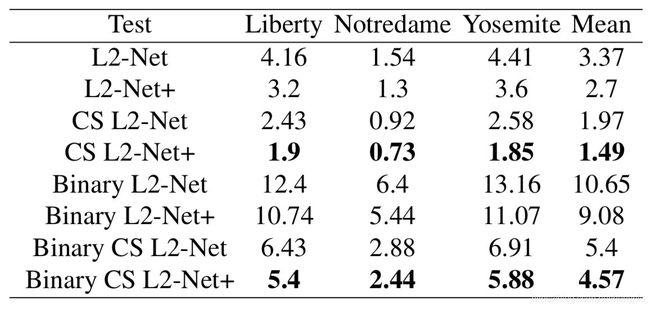
其中 + 表示做了 data augmentation。

其中 Binary 前缀表示根据 float 描述符的正负进行二值化，得到的 binary 的描述符，并比较性能。

同时本文还在 HPatches 上 train，在 Brown 数据集上 test，结果如下图所示：

Oxford

为了验证方法的泛化能力，在 Oxford 数据集上进行测试。在该数据集的 6 个图像序列上进行测试，分别是 graf (viewpoint)，bikes(blur)，ubc(JPEG compression)，leuven(light)，boat(zoom 和 rotation) 和 wall(viewpoint)。每个图像序列包括 6 张图像，每个序列是按照相对于第一张图像 distortions 程度递增的序列排列。在测试过程中，图像中的 keypoints 是用 Harris-Affine 方法检测得到，patches 统一归一化到 $32\times 32$ 大小(对于 DeepDesc 和 TNet-TGLoss 大小是 $64\times 64$)。文中说 scale=3 不理解啥意思。

其中这里主要比较的是 $mAP$。

竖直分隔线前面表示都在 Liberty(来自 Brown) 数据集上训练（DeepDesc 除外，是在 Liberty 和 Notredame 两个数据集上训练）。从中可以看出， CS 结构不能完全保证性能的提高，主要是因为 CS 结果需要 crop patch 的中间部分，怎么取选择 patch 的scale 是一个问题。Brown 和 Hpatches 数据集的 patches 基本是 scale 比较类似，所以效果比较好。但是应用到不同的检测器以及 scale 上，可能任意 crop (patch 的 50%) 出来的包含的纹理信息很少，所以导致效果不好。本文从结果中还发现，CNN 特征学习的方法对 blur 的情况比较敏感。咋解释？？

竖直线后面的表示本文提出的方法分别在 Liberty，Notredame，Yosemite 和 HPatches 上训练，在 Oxford 测试的性能结果。从结果可以看出，在 HPatches 数据集上训练的网络泛化性能更好。

HPatches

关于 HPatches 数据集的评测结果，具体查看 [2016 DescrWorkshop][http://icvl.ee.ic.ac.uk/DescrWorkshop/]，L2-Net 方法在 HPatches 上三个任务上都是第一。

实用指南

compactness 的重要性

本文实验过在训练过程不加 $E_2$，结果导致训练不收敛。文中给的解释是，如果没有 $E_2$ 的限制会导致 overfitting 比较严重，然后特征向量维度直接的关联性也比较大。

相对 distance 的优势

本文使用的 $E_1$ 和 之前的 hinge loss 有很大的区别， patch pair 和 triplet 的 hinge loss 如下：

$$\begin{array}{l}{E}_{pair}={\delta }_{ij}\max \left(0,{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }_2-t_p\right)+\left(1-{\delta }_{ij}\right)\max \left(0,t_n-{\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\Vert }_2\right)\\ E_{triplet}=\max \left(0,1-\frac{{\Vert {\mathbf{y}}_i-{\mathbf{y}}_i^{-}\Vert }_2}{{\Vert {\mathbf{y}}_i-{\mathbf{y}}_i^{+}\Vert }_2+t}\right)\end{array}$$

其中 ${\delta }_{ij}=1$，如果 $y_i$ 和 $y_j$ 匹配上，反之 ${\delta }_{ij}=0$。

其中 $t_p$，$t_n$ 和 $t$ 都是阈值参数。

这两个公式比较好理解，这里就不详细解释了，该 loss 主要的缺点是由于阈值导致的不稳定的梯度。而且不能确定一个 training batch 里面多少样本对整体梯度起作用，这样不稳定的梯度很可能导致优化到坏的局部最小。所以后面很多工作希望用 hard sample mining 来解决这个问题，但也会带来一个更严格的采样阈值。而使用相对 distance 不涉及到绝对的 distance，所以不会引入阈值。

DIF 的有效性

第一种测试，在实际训练中移除 $E_3$ 来验证 DIF 的有效性；第二种测试，在实际训练的每个 BN 层后面都加入 DIF 测试性能。比较结果如下图所示：

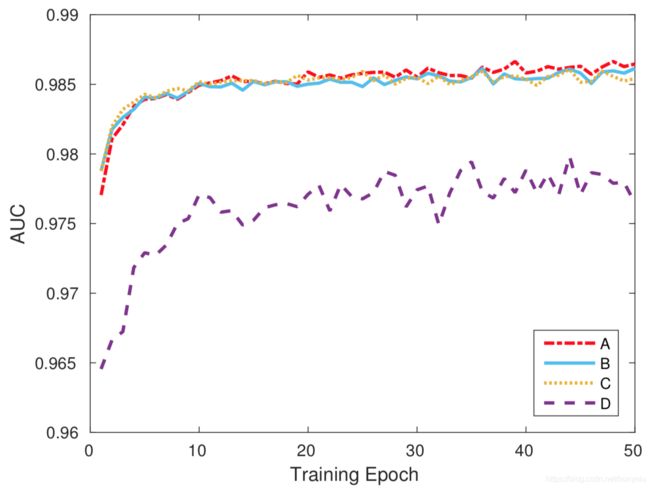
其中 AUC 具体含义参考：ROC曲线和AUC值

其中这里显示的是 L2-Net 是在 Hpatches 数据集上然后在 Brown 数据集上测试的结果（三个子集的平均值）。

其中 Curve A 表示默认配置，Curve B表示不加 DIF，即不加 $E_3$ ，Curve C 表示设置 BN 层参数为可学习的（用于验证 BN 不同条件下的效果），Curve D 表示每个 BN 层后面都加入 DIF 测试性能。

从上面结果可以看出，加上 DIF 确实比不加效果要好一点。 但感觉作用没有那么大？？？ 而且加多了明显效果会变差，文中解释说是限制了网络的解空间。。。

BN 层

在上面一节中 Curve A 和 Curve C 的对比，发现性能变化不大。

假设 $a\sim N\left({\mu }_1,{\sigma }_1\right)$ 和 $b\sim N\left({\mu }_2,{\sigma }_2\right)$ 为两个随机的服从高斯分布的变量。如果要区分这两个变量，最简单的方法就是增加 $\left|{\mu }_1-{\mu }_2\right|$ 以及减少 $\left|{\sigma }_1\right|$ 和 $ \left| \sigma _ { 2 } \right|$，其实就是增加两个高斯的 bias，减少分布的不同。同理学习 BN 的两个参数就会导致学习到的描述符非常 sharp 而且都是非零分布，这样破坏了描述符的性能。而固定则表示每个 patch 的 feature maps 都是独立分布的，这样网络就会学习分布的不同，而不是 bias的不同。

Binary 描述符

虽然说 binary 描述符是从 float 描述符简单的生成的，但这里也想给出一些说明。从不同的 3D 点中随机选取 $100K$ 个 patches 去探索生成的描述符中值的分布情况。分布结果如下图所示：

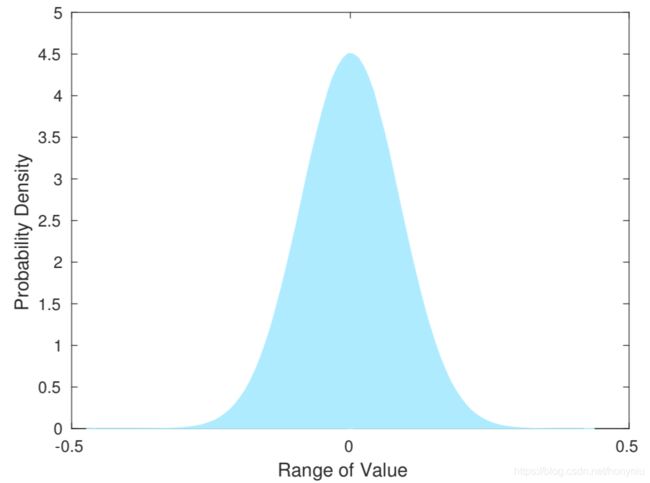
可以看出描述符的值服从 mean 为 0 的高斯分布。

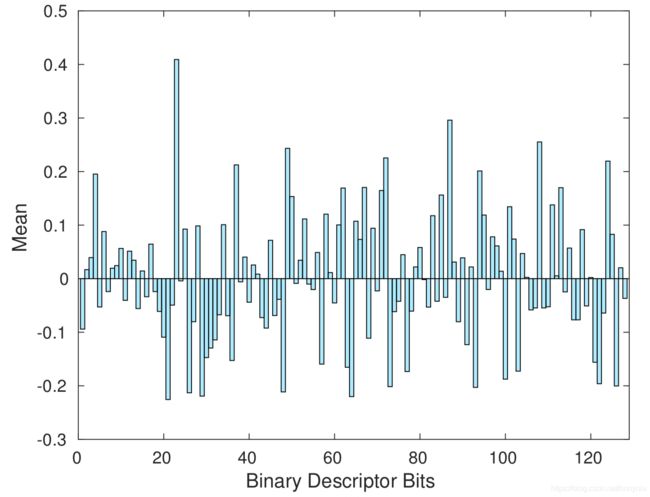
Binary 描述符每个 bit 在大量 patches 上的均值非常靠近 0，这是一个好的 binary 描述符具有的属性。具体结果如下图所示：

训练和提取速度

训练速度参考论文，提取速度为 $21.3Kpatch/sec$，在 GTX 970 GPU 上。