1. 什么是树状数组
顾名思义,就是用数组来模拟树形结构呗。那么衍生出一个问题,为什么不直接建树?答案是没必要,因为树状数组能处理的问题就没必要建树。和Trie树的构造方式有类似之处。
2. 树状数据解决什么问题
树状数据解决大部分基于区间上的更新以及求和问题.
3. 树状数组和线段树区别在哪里
树状数组可以解决的问题都可以用线段树解决,这两者的区别在哪里呢?树状数组的系数要少很多,就比如字符串模拟大数可以解决大数问题,也可以解决1+1的问题,但没人会在1+1的问题上用大数模拟。
4. 树状数组的优点和缺点
修改和查询的复杂度都是O(logN),而且相比线段树系数要少很多,比传统数组要快,而且容易写。
缺点是遇到复杂的区间问题还是不能解决,功能还是有限。
5. 树状数组介绍
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
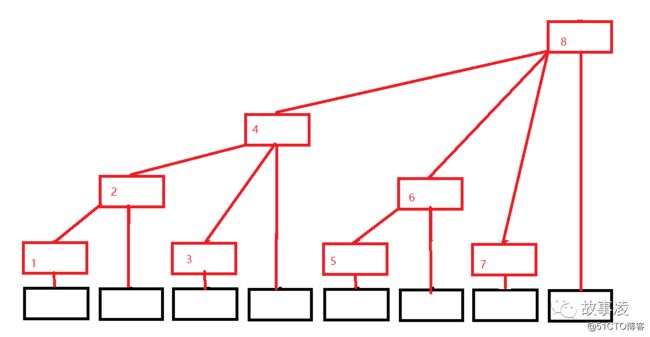
好了, 百度给了一个这么牛逼的概念, 那我们如何理解呢? 要不然你看着这一堆字就头疼, 好吧, 我来帮你解决吧, 其实就是一个数组A[i], 而我自己又重新创建一个数组C[i], 用来记录A[i]数组对应的下标的和, 如果只是简单的下标求和, 那就太简单了, 还搞什么树状数组, 下面就来看看这个骚操作吧, 大概就是长这个样子的.
黑色数组代表: A[i]
红色数组代表: C[i]
但是, C[i]和A[i]之间是有一定关系的, 后面我们会介绍, 你先知道树状数组, 其实也没什么难的, 就是这个套路就好了!
6. 我们通过例子来分析
这里通过一个简单的题目展开介绍,先输入一个长度为n的数组,然后我们有如下两种操作:
-
输入一个数m,输出数组中下标1~m的前缀和
- 对某个指定下标的数进行值的修改
多次执行上述两种操作
6.1 寻常方法
对于一个的数组,如果需要求1~m的前缀和我们可以将其从下标1开始对m个数进行求和,对于n次操作,时间复杂度是O(n^2),对于值的修改,我们可以直接通过下标找到要修改的数,n次操作时间复杂度为O(n),在数组n开得比较大的时候,求前缀和的效率显得低了.
6.2 简单的优化
初始我们用一个数组A的保存每个位置的初始值,然后用一个辅助数组B存放的是下标为i的时候A数组的前i个的和(前缀和),那么当我们需要查询m个数的前缀和的时候只要直接使用下标对B数组进行查询即可,n次查询,时间复杂度为O(n),而此时,对于单点更新值的维护消耗,由原来的O(n)变成了O(n^2),因为每一次与更新单点值都会对后面的已经计算好的B数组前缀和的值造成影响,需要不断更新B数组的值,n次更新维护的消耗自然就变成了O(n^2),更新的效率变得低下
7. 树状数组来解题
如上图,对于一个长度为n的数组,A数组存放的是数组的初始值,引入一个辅助数组C(我们通过C数组建立树状数组
C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8为什么要有这样的计算方法呢? 别急, 我先来告诉大家一个方法:
我们首先, 先把i 换算成二进制的运算模式, k为i的二进制的末尾0的个数
i = 1 二进制: 0, k = 0
i = 2 二进制: 10, k = 1
i = 3 二进制: 11, k = 0
i = 4 二进制: 100, k=2
i = 5 二进制: 101, k=0
i = 6 二进制: 110, k=1
i = 7 二进制: 111, k=0
i = 8 二进制: 1000, k=3
7.1 C[i]和A[i]的对应关系是什么呢?
我们称C[i]的值为下标为i的数所管辖的数的和,C[8]存放的就是被编号8所管辖的那些数的和(有8个)
下标为i的数所管辖的元素的个数则为2^k个(k为i的二进制的末尾0的个数)
举两个例子查询下标:
m==8和m==5所管辖的数的和
8 = 1000,末尾3个0,故k == 3,所管辖的个数为2^3 == 8,C8是8个数的和
5 = 0101,末尾没有0,故k == 0,所管辖的个数为2^0 == 1,C5是一个数的和(它本身A5)7.2 求m前缀和
而对于输入的数m,我们要求编号为m的数的前缀和A1~Am(这里假设树状数组已经建立,即C1~C8的值已经求出,别着急,在本文的最下方会做出建立树状数组的过程讲解,因为现在是在求前缀和,就假设C数组已经可用了吧)
举两个例子m==7和m==6(sum(i)表示求编号为i的前缀和)
m==7
sum(7) = C7 + C6 + C4那么我们是怎么得到编号7是由哪几个C[i]求和得到呢(C4, C6, C7怎么得到的?
这里有介绍一种巧妙的方法:对于查询的m,将它转换成二进制后,不断对末尾的1的位置进行-1的操作,直到全部为0停止
- 7的二进制为0111(C7得到)
- 那么先对0111的末尾1的位置-1,得到0110 == 6(C6得到)
- 再对0110末尾1位置-1,得到0100 == 4(C4得到)
- 最后对0100末尾1位置-1后得到0000(结束信号),计算停止
- 至此C7,C6,C4全部得到,求和后就是m == 7时它的前缀和
如果还没有看懂, 我们再来看一个例子:
m==6
sum(6) = C6 + C4-
m == 6时也是一样,先转成2进制等于0110,
-
经过一次变换后为0100(C4)
-
在经过一次变化后0000(结束信号)
- 那么求和后同样也得到了sum(6) = C6 + C4
7.2.1 使用位操作高效计算
这里要介绍一个高效的方法,lowbit(int m),这是一个函数,它的作用是求出m的二进制表示的末尾1的位置,对于要查询m的前缀和,m = m - lowbit(m)代表不断对二进制末尾1进行-1操作,不断执行直到m == 0结束,就能得到前缀和由哪几个Cm构成,十分巧妙,lowbit也是树状数组的核心
int lowbit(int m){
return m&(-m);
}关于m&(-m)很多童鞋可能感到困惑,那么就不得不提及一下负数在计算机内存中的存储形式,负数在计算机中是以补码的形式存储的.
例如: 我们来拿13做个例子
- 13的二进制表示为1101,末尾没有0, 即他本省C[13].
- 那么-13的二进制而将13二进制按位取反,然后末尾+1,即0010 + 0001 = 0011,那么1101 & 0011== 0001,很显然得到m == 13二进制末尾1的位置是2的0次方位,将13 - 0001 == 12, 即C[12]
- 再对12执行lowbit操作,1100 & 0100 == 0100,也很轻易得到了m == 12时二进制末尾1的位置是2的2次方位,将12 - 0100 == 8,即C[8]
- 再对8执行lowbit操作,0100 & 1100 == 0100,得到m == 8时二进制位是2的2次方位,8 - 0100 == 0(结束操作)
- 通过循环得到的13,12,8,则sum(13) == C13 + C12 + C8
求前缀和的代码
int ans = 0;
int getSum(int m){
while(m > 0){
ans += C[m];
m -= lowbit(m);
}
}对于n次前缀和的查询,时间复杂度为O(nlogn)
7.3 单点更新值
对于输入编号为x的值,要求为它的值附加一个value值(所以有他的局限性),我们把图再一次拿下来
现在我们需要把A[2]更改值加上5: 即: A[2] = A[2] + 5, 那我们同时, 是不是也需要更新C[n]的一些列操作呢?那应该如何做呢?
- 首先我们先找到A[2]的位置,通过观察上面计算的结算结果我们得知,如果修改了A[2]的值,那么管辖A[2]的C[2],C[4],C[8]的前缀和都要加上value(所有的祖先节点),
- 那么和查询类似,我们如何得到C2的所有祖先节点呢(因为C2和A2的下标相同所以更新时查询从C[x]开始),依旧是上述的巧妙的方法,但是我们把它倒过来对于要更新x位置的值,我们把x转换成二进制,不断对二进制最后一个1的位置+1,直到达到数组下标的最大值n结束
- 对于给出的例子x==2,假设数组下标上限n==8,x转换成二进制后等于0010(C2),对末尾1的位置进行+1,得到0100(C4),对末尾的1的位置进行+1,得到1000(C8),循环结束,对C2,C4,C8的前缀和都要加上value,当然不能忘记对A[2]的值+value,单点更新值过程结束
给出代码
void update(int x, int value){
A[x] += value; //不能忘了对A数组进行维护,尽善尽美嘛
while(x <= n){
C[x] += value;
x += lowbit(x);
}
}对于n次更新操作,时间复杂度同样为O(nlogn)
这里有一个注意事项,我们对于求前缀和与单点更新时,树状数组C是拿来直接使用的,那么问题来了,树什么时候建立好的,我怎么不知道??
7.4 如何创建树状数组
事实上,对于一个输入的数组A,我们一次读取的过程,就可以想成是一个不断更新值的过程(把A1~An从0更新成我们输入的A[i]),所以一边读入A[i],一边将C[i]涉及到的祖先节点值更新,完成输入后树状数组C也就建立成功了
- 完整代码如下:
#include
#include
int a[10005];
int c[10005];
int n;
int lowbit(int x){
return x&(-x);
}
int getSum(int x){
int ans = 0;
while(x > 0){
ans += c[x];
x -= lowbit(x);
}
return ans;
}
void update(int x, int value){
a[x] += value;
while(x <= n){
c[x] += value;
x += lowbit(x);
}
}
int main(){
while(scanf("%d", &n)!=EOF){ //用于测试n == 8
memset(a, 0, sizeof(a));
memset(c, 0, sizeof(c));
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]); //a[i]的值根据具体题目自己安排测试可以1,2,3,4,5,6,7,8
update(i, a[i]); //输入的过程就是更新的过程
}
int ans = getSum(n-1); //用于测试输出n-1的前缀和 输出28
printf("%d\n", ans);
}
return 0;
} 故事凌
明天能否加个鸡腿!
稀罕作者