M序列与加扰器

（一）m序列

码分多址系统需要具有良好自相关性的二进制数序列作为码，即要求码与其本身的平移正交。为了减少噪声和其他码对一个码的自相关运算的干扰，我们要求码看上去最好是随机的。二进制数随机序列能满足这一个条件，但是由于它不能复制而很难在实际中加以利用。伪随机噪声码（PRN）简称伪随机码或者伪码，它不但是一种能预先确定的、有周期性的二进制数序列，而且又具有接近于二进制数随机序列的良好自相关特性。

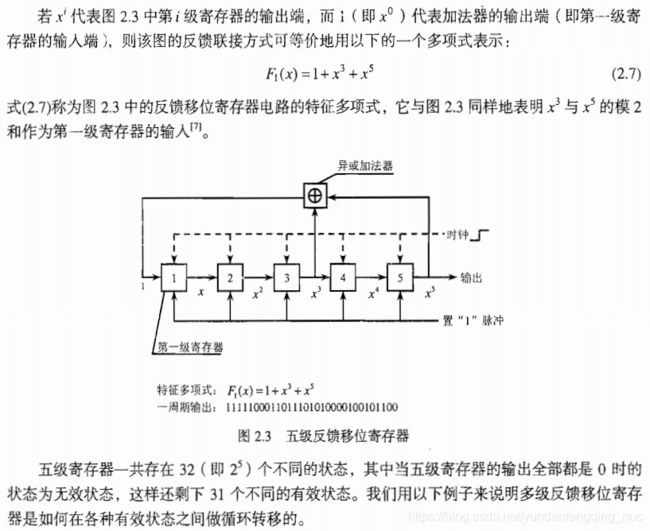
这种周期性的伪随机码可由一个多级反馈移位寄存器产生。图2.3所示是一个五级反馈移位寄存器电路，其中第一级寄存器位于电路的最左边，而第三级和第五级寄存器输出值的异或相加结果反馈作为第一级寄存器的输入。通常，最后一级寄存器的输出端用做整个多级反馈移位寄存器的伪随机码输出端。

M序列的输出为：最后一级寄存器的输出端（x^5）作为整个电路的输出端。

(二) 扰码原理

扰码器的输出为：S(x)^输入数据。

这里和M序列的输出不一样。

M序列matlab仿真：

clc;
clear all;
close all;
%%初始化
m(1,1) = 1;
m(1,2) = 1;
m(1,3) = 1;
m(1,4) = 1;
m(1,5) = 1;
for i = 1:1:31 
    b(1,i) = m(1,5);
    a(1,i) = mod((m(1,5) + m(1,3)+m(1,2)+m(1,1)),2);
    m(1,5) = m(1,4);
    m(1,4) = m(1,3);
    m(1,3) = m(1,2);
    m(1,2) = m(1,1);
    m(1,1) = a(1,i);
    m
end
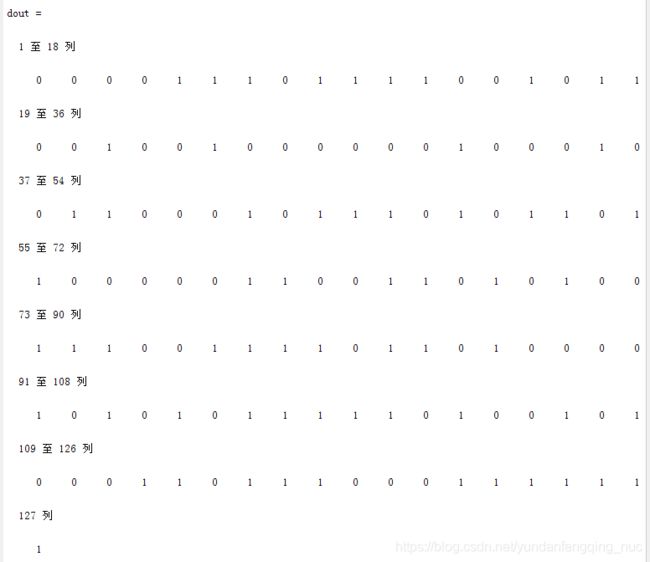
dout = b

加扰器matlab仿真：

clc;
clear all;
close all;
d(1,1) = 1;
d(1,2) = 1;
d(1,3) = 1;
d(1,4) = 1;
d(1,5) = 1;
d(1,6) = 1;
d(1,7) = 1;
for i = 1:1:127 
    a(1,i) = mod((d(1,7) + d(1,4)),2);
    d(1,7) = d(1,6);
    d(1,6) = d(1,5);
    d(1,5) = d(1,4);
    d(1,4) = d(1,3);
    d(1,3) = d(1,2);
    d(1,2) = d(1,1);
    d(1,1) = a(1,i);
    d;
end
dout = a