离散数学基础——（1）排列组合

阶乘

       阶乘是基斯顿·卡曼（Christian Kramp，1760～1826）于 1808 年发明的运算符号，表示一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积。

例如1的阶乘为1，3的阶乘为6，并且0的阶乘为1。

自然数n的阶乘写作n!，n!=1×2×3×...×(n-1)×n。

阶乘以递归方式定义，即：

                0!=1；

                n!=(n-1)!×n；

加法原理

        加法原理是分类计数原理，常用于排列组合中，具体是指：做一件事情，完成它有n类方式，第一类方式有M1种方法，第二类方式有 M2 种方法，……，第n类方式有Mn种方法，那么完成这件事情共有 M1+M2+…+Mi+…+Mn 种方法。

可能理论有些晦涩难懂，举个例子：

        从小明家到学校有3种交通方式，走路、骑车、坐公交，在这其中，他只走1条路径，骑车也只走最近的路（1条），但坐公交有2路车。

        容易得，小明从家到学校有 (1+1+2)=4 种。

乘法原理

      做一件事，完成它需要分成n个步骤，做第一 步有 M1 种不同的方法，做第二步有 M2 种不同的方法，……，做第n步有Mn种不同的方法。那么完成这件事共有 M1×M2×M3×…×Mn 种不同的方法。乘法原理和加法原理是数学概率方面的基本原理。

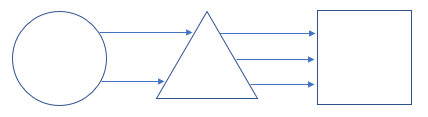
        如上图，从圆出发到正方形共有 2 个步骤，即 圆→三角形→正方形 ，从圆到三角形共有 2 条路径，从三角形到正方形有 3 条路径。

        容易得，从圆出发到正方形共有 (2×3)=6 种。

排列

        已知，现有 54 名学生排队，老师要求从中选取 10 人排队，请问排队的结果有多少种？

由题意可知：

        对于队列中的第 1 个位置，有 54 个人选；

        对于队列中的第 2 个位置，有 53 个人选；

        对于队列中的第 3 个位置，有 52 个人选；

        ......

        对于队列中的第 10 个位置，有 45 个人选。

所以，对于此题，排队的结果共有 (54×53×52×...×45)=86,839,771,951,296,000 种。

        

        已知，现有 n 名学生排队，老师要求从中选取 k 人排队，请问排队的结果有多少种？

由题意可知：

        对于队列中的第 1 个位置，有 n 个人选；

        对于队列中的第 2 个位置，有 (n-1) 个人选；

        对于队列中的第 3 个位置，有 (n-2) 个人选；

        ......

        对于队列中的第 k 个位置，有 (n-k+1) 个人选。

所以，对于此题，排队的结果共有 [n×(n-1)×(n-2)×...×(n-k+1)] 种。

上述结果实在太长，不便书写，此时我们可使 结果的分子、分母 同时乘 [(n-k)×(n-k-1)×...×1] ，即 (n-k)! ，也可得出正确结果。

在数学中，我们将它称为排列，用下列式子表示。

（注：当k=n时，我们称之为全排列）

组合

         已知，现有 n 名学生排队，老师要求从中选取 k 人作为辩手参加辩论赛，请问最终人选有多少种？

与排列相比，组合同样是从大部分中选出小部分，但却无需分出被选人之间的位置关系。

根据乘法原理，我们可以将组合记作 C ，用式子表示为：

由上述式子，我们还可以得出组合的两个性质：

性质 1 证明：

证明方法1：

       

证明方法2：

       考虑实际意义，显然， "从 n 个 人中选择 k 个人出来" 等价于 "从 n 个 人中选择 (n-k) 个人不出来"

所以 性质 1 成立。

性质 2 证明：

证明方法1：

证明方法2：

       考虑实际意义，显然，对于 1 个人只有选或不选两种可能，选的话只需从 (n-1) 个人中再选出 (k-1) 个人，不选的话只需从 (n-1) 个人中再选出 k 个人。

       根据加法原理，可得

所以 性质 2 成立。