排序算法总结(三)
一、前言
本篇博客属于对排序算法的复习,主要是基于《算法》一书。本文将要介绍的是堆排序以及基于二叉堆的优先队列的实现
注: 本文中所有的图片均为《算法》一书的辅助图片,代码实现也源自该书。
本文只是对其要点的提炼,想要详细的学习这些算法请自行观看相关书籍。
二、正文
本篇文章将要复习的知识点为堆排序,在此之前我们要先学习堆排序所依赖的一个很重要的抽象数据类型——优先队列,然后再学习基于优先队列的堆排序。
1. 优先队列
优先队列是一种抽象数据类型,表示了一组值和对这些值的操作,以最大优先队列为例,它最重要的两个操作就是 删除最大元素 和 插入元素,它的 API 如下表所示:

1.1 思想
在本文中我们的优先队列是基于二叉堆实现的,二叉堆能够很好地实现优先队列的基本操作。在二叉堆的数组中,每个元素都要大于等于另外两个特定位置的元素。而如果我们将二叉堆画成一棵二叉树,那么当二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序,下图即为一棵堆有序的完全二叉树图:
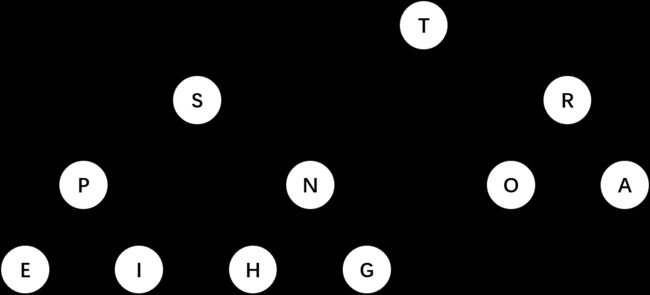
在我们的实现中,将采用数组的方式来实现二叉堆。在一个二叉堆中,位置 k \ k k 的结点的父结点的位置为 ⌊ k / 2 ⌋ \ \lfloor k/2 \rfloor ⌊k/2⌋,而它的两个子结点的位置则为 2 k \ 2k 2k 和 2 k + 1 \ 2k+1 2k+1。这样我们就只需要通过计算数组的下标就可以在树中上下移动:从 a[k] 向上一层就令 k \ k k 等于 k / 2 \ k/2 k/2,向下一层则令 k \ k k 等于 2 k \ 2k 2k 或 2 k + 1 \ 2k+1 2k+1。
并且我们规定数组中的位置 0 不存放元素,如上图中我们将 T 的下标定为 1,那么 S 的下标即为 2,R 的下标即为 3,依次类推,如下图所示:
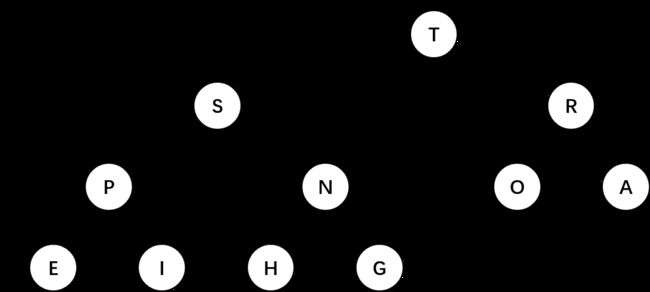
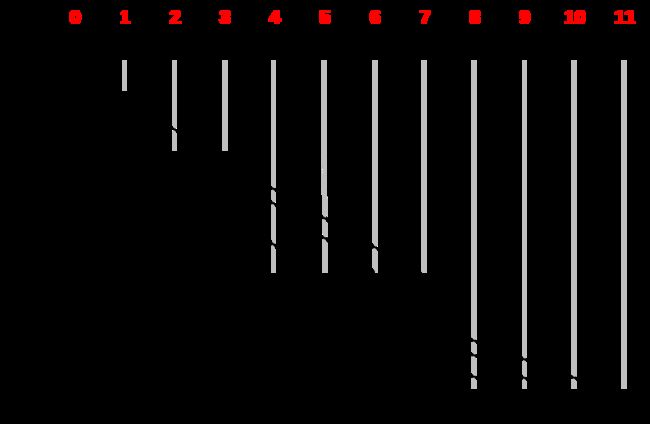
从上述图形中我们可以看出当 N \ N N 达到 2 的幂时书的高度会加 1,由此我们可以得出一个结论:一棵大小为N的二叉树高度为 ⌊ l g N ⌋ \ \lfloor lgN \rfloor ⌊lgN⌋。
1.2 代码实现
由于我们是采用数组的方式构造二叉堆的,所以在二叉堆的数据结构中我们就只需维护一个大小为 N + 1 \ N+1 N+1 的数组 pq[ ] 即可(位置0不会被使用,所以需要加1)。
1.2.1 恢复堆有序
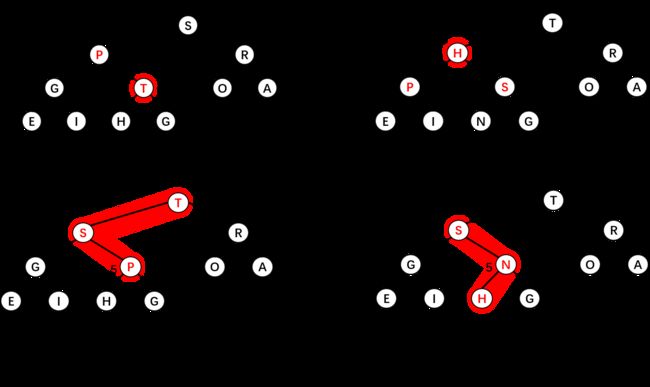
接下来需要考虑的就是堆有序的问题。当某个结点优先级上升时,例如插入一个新元素,一般情况下我们会先将该元素插入至数组尾部,上图中插入一个字母 Z 的话,它此时位于数组下标 12 的位置上,此时的堆不是有序的,我们需要由下至上恢复堆的顺序。
而当某个结点优先级下降时,例如根节点(即下标为1的结点)替换为一个较小的元素时,此时的堆也不是有序的,我们就需要由上至下恢复堆的顺序。
由下至上的操作我们称之为上浮(swim),而上至下的操作我们称之为下沉(sink),它们的代码如下所示:
// 上浮
private void swim(int k){
while (k > 1 && less(k/2, k)){
exch(k/2, k);
k = k/2;
}
}
// 下沉
private void sink(int k){
while (2*k <= n){
int j = k*2;
// 从左右子结点中挑出较大的元素和k进行比较
if (j < n && less(j, j+1))
j++;
// 如果此时 pq[k] >= pq[j],那么该堆有序,操作终止
if (!less(k, j))
break;
exch(k, j);
k = j;
}
}
private boolean less(int i, int j){
return comparator == null ? ((Comparable<E>)pq[i]).compareTo(pq[j]) < 0
: comparator.compare(pq[i], pq[j]) < 0;
}
private void exch(int i, int j){
E temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
1.2.2 插入和删除最大元素
有了上面提供的上浮和下沉操作,插入和删除最大元素的操作将会变的非常简单。
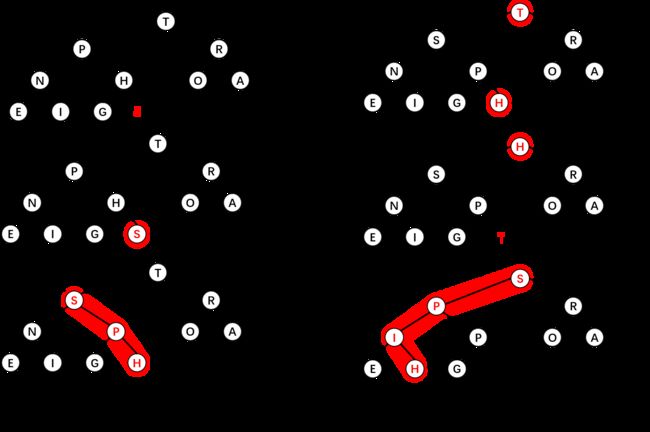
插入元素时,我们将新元素插入到数组末尾,然后让这个新元素上浮到合适的位置即可。由于我们采用的是数组存储元素,因此还需要考虑数组的扩容问题,即动态数组。
删除最大元素时,我们的做法是直接将数组的最后一个元素放到顶端,减少堆的大小并让这个元素下沉到合适的位置。
插入和删除最大元素的代码实现如下:
// 插入
public void insert(E e){
// 当数组已满时将数组大小扩充为原来的2倍
if (n == pq.length - 1){
resize(2*pq.length);
}
pq[++n] = e;
swim(n);
}
// 删除最大元素
public E delMax(){
E max = pq[1]; // 从根结点获得最大元素
exch(1, n--); // 将其与最后一个元素交换
pq[n+1] = null; // 便于GC
sink(1); // 下沉
return max;
}
// 扩容
private void resize(int capacity){
E[] newPq = (E[]) new Object[capacity];
for (int i = 1; i < pq.length; i++){
newPq[i] = pq[i];
}
pq = newPq;
}
1.2.3 完整的代码实现
基于堆的最大优先队列代码如下所示:
public class MaxPQ<E> {
private E[] pq; // 基于堆的完全二叉树
private int n; // 存储于pq[1...n]中,pq[0]没有使用
private Comparator<E> comparator; // 自定义比较器
public MaxPQ(int initCapacity){
pq = (E[]) new Object[initCapacity+1];
n = 0;
}
public MaxPQ(){
this(1);
}
public MaxPQ(int initCapacity, Comparator<E> comparator){
pq = (E[]) new Object[initCapacity];
n = 0;
this.comparator = comparator;
}
public MaxPQ(Comparator<E> comparator){
this(1, comparator);
}
public void insert(E e){
if (n == pq.length - 1)
resize(2*pq.length);
pq[++n] = e;
swim(n);
}
public E delMax(){
E max = pq[1];
exch(1, n--);
pq[n+1] = null;
sink(1);
return max;
}
public E max(){
if (isEmpty())
throw new NoSuchElementException("Priority Queue is underflow");
return pq[1];
}
public boolean isEmpty(){
return n == 0;
}
public int size(){
return n;
}
private void resize(int capacity){
E[] newPq = (E[]) new Object[capacity];
for (int i = 1; i < pq.length; i++){
newPq[i] = pq[i];
}
pq = newPq;
}
private boolean less(int i, int j){
return comparator == null ? ((Comparable<E>)pq[i]).compareTo(pq[j]) < 0
: comparator.compare(pq[i], pq[j]) < 0;
}
private void exch(int i, int j){
E temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
private void swim(int k){
while (k > 1 && less(k/2, k)){
exch(k/2, k);
k = k/2;
}
}
private void sink(int k){
while (2*k <= n){
int j = k*2;
// 从左右子结点中挑出较大的元素和k进行比较
if (j < n && less(j, j+1))
j++;
// 如果此时 pq[k] >= pq[j],那么该堆有序,操作终止
if (!less(k, j))
break;
exch(k, j);
k = j;
}
}
}
1.3 复杂度分析
对于一个含有 N \ N N 个元素的基于堆优先队列,插入元素操作只需不超过 ( l g N + 1 ) \ (lgN+1) (lgN+1) 次比较,删除最大元素的操作需要不超过 2 l g N \ 2lgN 2lgN 次比较。
证明。插入操作和删除最大元素的操作都需要在根结点和堆底之间移动元素,而路径长度不超过 l g N \ lgN lgN。对于路径上的点,删除最大元素操作需要两次比较(除了堆底元素),一次用来找出较大的子结点,一次用于确定该子结点是否需要上浮。
1.4 优先队列的经典应用
优先队列的最典型应用就是解决 TopM 问题。
输入 N \ N N 个字符串,每个字符串都对应着一个整数,从中找出最大的(或是最小的) M \ M M 个整数。
这个问题最简单的思路就是先将这些数据进行排序,然后再从排好序的数组中输出前 M \ M M 个数即为我们想要的结果。但是在 N ≫ M \ N \gg M N≫M 的情况下(例如 N = 100000 , M = 10 \ N=100000, M=10 N=100000,M=10),这种做法的代价会非常高昂,因为我们并不是需要整个数组有序。这就是典型的 TopM 问题。
在这种情况下,我们就可以考虑使用优先队列来处理这个问题,我们这里输出的是最小的 M \ M M 个整数,代码如下所示:
public class TopM {
public static void main(String[] args) throws FileNotFoundException {
int M =10; // 打印输入流中最小的M个单词
MaxPQ<String> pq = new MaxPQ<>(M+1);
Scanner scanner = new Scanner(new File("src/com/marck/sort/tale.txt"));
while (scanner.hasNext()){
String word = scanner.next();
pq.insert(word);
if (pq.size() > M){
pq.delMax(); // 如果优先队列中存在M+1个元素就删除其中最大的元素
}
} // while执行完毕之后最小的M个元素就都留在优先队列中了
while (!pq.isEmpty()){
System.out.print(pq.delMax() + " ");
}
}
}
在这段代码中,我们通过构造一个大小为 M + 1 \ M+1 M+1 的最大优先队列,每当优先队列中的元素个数到达 M + 1 \ M+1 M+1 时,我们就删除最大的元素,这样在数据流读取完毕之后,在优先队列中存储的 M \ M M 个元素即为最小的,下面附上排序算法和优先队列在处理 TopM 问题上的增长数量级:

而对于从数据流中找出最大的 M \ M M 个元素的问题,我们就可以采用最小优先队列来实现了。最小优先队列 MinPQ 和 MaxPQ 的代码几乎一致,唯一的区别仅在于 MinPQ 比较所采用的是 greater() 方法而不是 less() 方法,greater() 方法在第一个元素大于第二个元素时返回 true,其他情况返回 false。只要将 MaxPQ 中所有用到 less() 方法的地方替换成 greater() 方法,我们很容易地就能得到一个最小优先队列了。
2. 堆排序
2.1 思想
堆排序是一种基于优先队列的排序方式,它可分为两个阶段:
- 堆构造阶段。将原始数组进行相关操作,从而使得原始数组堆有序。
- 下沉排序阶段。从堆中按递减顺序取出所有元素并得到排序结果。
对于堆的构造来说,只需从左到右遍历数组,用 swim() 保证扫描指针左侧的所有元素已经是一棵堆有序的完全树即可,就像连续向优先队列中插入元素一样,这种方式所花时间和 N l o g N \ NlogN NlogN 成正比。
一种更高效的方式是从右至左用 sink() 方法构造子堆。数组的每个位置都已经是一个子堆的根结点了,如果一个结点的两个子堆都已经是堆了,那么在该结点上调用 sink() 可以将它们变为一个堆。所以开始时我们只需扫描数组中一半的元素,因为我们可以跳过大小为 1 的子堆,然后逐步往上构造堆,直到最后在位置 1 上调用 sink() 方法时,扫描结束,此时堆也构造完成了。
2.2 代码实现
基于上述思想,我们可以得到如下代码实现:
public class HeapSort {
public static void sort(Comparable[] a){
int n = a.length;
// 1.堆的构造
for (int k = n/2; k >= 1; k--){
sink(a, k, n);
}
// 2.下沉排序
while (n > 1){
exch(a, 1, n--);
sink(a, 1, n);
}
}
private static void sink(Comparable[] a, int k, int n){
while (2*k <= n){
int j = 2*k;
if (j < n && less(a, j, j+1))
j++;
if (!less(a, k, j))
break;
exch(a, k, j);
k = j;
}
}
private static boolean less(Comparable[] a, int i, int j){
return a[i-1].compareTo(a[j-1]) < 0;
}
}
在这段代码中,sink()、exch() 和 less() 方法均被改造过 ,sink() 方法用将 a[1] 到 a[n] 的元素排序,exch() 和 less() 的实现中的索引减 1 即可得到和其他排序算法一致的实现(将a[0]至a[n-1]排序)。
我们以对数组 [ S O R T E X A M P L E ] 进行排序为例展示堆排序的运行轨迹,如下图所示:

2.3 复杂度分析
用下沉操作由 N \ N N 个元素构造堆只需要少于 2 N \ 2N 2N 次比较以及少于 N \ N N 次交换。
证明。例如构造一个63个元素的堆,我们会处理16个大小为3的堆,8个大小为7的堆,4个大小为的堆,2个大小为31的堆和1个大小为63的堆,因此最坏情况下需要 16 × 1 + 8 × 2 + 4 × 3 + 2 × 4 + 1 × 5 = 57 \ 16\times1+8\times2+4\times3+2\times4+1\times5=57 16×1+8×2+4×3+2×4+1×5=57 次交换(以及两倍的比较)。
将 N \ N N 个元素排序,堆排序只需要少于 ( 2 N l g N + 2 N ) \ (2NlgN+2N) (2NlgN+2N) 次比较(以及一半次数的交换)。
2 N \ 2N 2N 项来自于堆的构造。 2 N l g N \ 2NlgN 2NlgN 项来自于每次下沉操作最大可能需要 2 l g N \ 2lgN 2lgN次比较。
2.4 堆排序的特点
堆排序是我们所知的唯一能够同时最优化地利用空间和时间的方法,在最坏的情况下它也能保证用 ∼ 2 N l g N \ \sim 2NlgN ∼2NlgN 次比较和恒定的额外空间。当空间时分紧张时(例如在嵌入式系统中)它很流行,因为它只用简短的几行就能实现较好的性能。
三、参考
- 《算法4th》
- 第2章 排序
- 2.4 优先队列
- 第2章 排序