高等数学上:微分中值定理,洛必达法则
此讲包括的内容很多,有闭区间上连续函数的零点存在定理,介值定理,还有微分中值定理中的费马定理,罗尔中值定理,拉格朗日中值定理,柯西中值定理
首先讲讲最基本的,零点存在定理和介值定理以及最值定理
最值定理:
内容:若一个函数f(x)在闭区间[a, b]上连续,那么它一定在区间[a, b]上存在最大值M和最小值m。
这个定理比较直观
介值定理:
内容:若一个函数f(x)在闭区间[a, b]上连续,那么对于任意[a, b]之间的一个点e,都有m <= f(e) <= M;其中m, M是区间[a, b]上的最小值和最大值。
这个定理是建立在最值定理之上的。也很显然。
通俗来讲,某一个区间内的函数值,肯定大于等于该区间内的最小值,肯定小于等于该区间内的最大值。
这两个定理虽然感觉是显而易见的,但要证明却不是很好证,涉及到实数的完整性,我们这里就不证了。
零点存在定理:
内容:设函数f(x)在闭区间[a, b]上连续,如果有f(a) * f(b) <0,那么在[a, b]之间一定存在一点k,使得f(k) = 0。
很容易发现,这个定理就是介值定理的一个特殊情况。
简单证明一下:
因为有介值定理
所以f(x)在闭区间[a, b]上一定存在最大值M和最小值m;
那么因为此时有f(a) * f(b) <0
假设f(a) < 0, f(b) > 0;
那么最大值M >= f(b);最小值m <= f(a);
又因为 f(b)为正,f(a)为负
所以M必定为正,m必定为负!
因此,根据介值定理,闭区间内任意一点e,满足m <= f(e) <= M
即f(e)介于一个正数和一个负数之间,又因为函数连续
所以必定存在一点k,有f(k) = 0;
好,那么到此第一部分闭区间上连续函数的几个性质就讲完了,现在进入微分中值定理:
在介绍费马定理之前,我们先介绍一下极大值和极小值的概念:
极大值与极小值:
定义:如果函数f(x)在x0点处,存在一个邻域U(x0, e),使得在这个邻域内的所有x对应的函数值f(x) >= f(x0),那么我们就把函数f(x0)称为函数在x0处的极小值,x0就是极小值点。如果这个邻域内的所有x对应的函数值f(x) <= f(x0),那么我们就把函数f(x0)称为函数在x0处的极大值,x0就是极大值点。
这个定义十分严谨,好好理解之后我们就可以辨别如下容易混淆的问题了
比如:
函数y = 1在[0, 2]上有没有极大值呀?
答案是:有! 因为根据定义,因为根据极值的定义,大于等于和小于等于即可,所以常函数上面一定是有极大值和极小值的!
再注意一点:只要存在一个邻域就可以了,如果是对于所有的邻域都有大于等于或小于等于关系,那很明显,就成了最大值或最小值了!
因此,由极值的定义,我们可以得出,最值也是极值,但极值不一定是最值。
费马定理:
内容:若函数f(x)在x0处可导,并且x0是函数f(x)的一个极值点,那么f(x)在x0处的导数一定为0。
几何意义:
极值点的切线是水平的。
定理证明:(根据左右导数和导数的定义)
对于一个极值点,不妨假设x0是极大值点(极小值证明完全一样)
那么,根据导数的定义:x0处的左导数为 = [ f(x) - f(x0) ] / [x - x0];
因为是左导数,所以此时的x小于x0,又因为f(x0)极大值
分母一定是负数,分子也是负数,最后的结果是一个非负数
结论1:x0处左导数为非负数
同理:x0处的右导数一样通过导数的定义算出,右导数是非正数!
由题目条件,函数在x0处可导,因此左右导数必然都相等
所以,左导和右导肯定都为0!
因此,x0处的导数为0!
罗尔中值定理:(重要)
我觉得它是三大微分中值定理中最重要的,是推导拉格朗日和柯西定理的基础
内容:若函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,并且满足f(a) = f(b),那么在区间(a, b)内必然存在一点k,使得f(x)在k这一点的导数为0。
几何意义:
如果满足条件,那么区间内肯定存在一点的切线水平。

证明:(运用费马定理)
首先关键条件f(a) = f(b);
那么说明,这个函数f(x)只可能有两种情况:
1.水平直线,常函数。2。有起伏的连续光滑曲线
如果是情况1:很明显,里面每一个点,都有导数为0,因为每一个点都可以做极值
因此每一个点都是满足费马定理的。
重点是情况2:
因为函数是闭区间上的连续函数,所以满足最值定理,即一定存在最大值M与最小值m
且M≠m,并且最大值和最小值至少有一个不在a, b取。否则就变成情况1了
因此,最大值M与最小值m都是极值点,即此时函数内部存在至少一个极值点
根据费马定理,得出结论,那个极值点的位置,导数为0。
所以,综上所述,罗尔定理是正确的。
接下来,我们看看罗尔中值定理的推广,拉格朗日中值定理
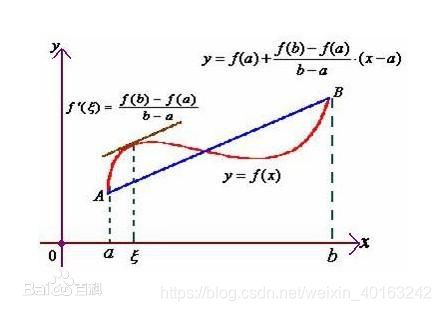
拉格朗日中值定理:
罗尔定理有三个条件,这里拉格朗日没有第三个必须f(a) = f(b)。只要满足前两个即可存在,所以也被称为罗尔中值定理的推广。
内容:若函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,那么区间(a, b)内一定存在一点k, 使得f '(k) = [f(b) - f(a)] / (b - a);
几何意义:
如果满足条件,那么区间内肯定有一点的切线斜率等于ab连线的斜率
定理证明:(运用罗尔中值定理)
运用罗尔定理证明的一般方法,因为式子里面出现了导数,我们就可以构造一个函数
F'(x) = f'(x) - [f(b) - f(a)] / (b - a);
∴F(x) = f(x) - [f(b) - f(a)] * x / (b - a);
将x = a与x = b带入,我们发现F(a) = F(b);
因此F(x)满足了罗尔中值定理
所以至少存在一点F'(k) = f'(k) - [f(b) - f(a)] / (b - a) = 0;
所以至少存在一点:f '(k) = [f(b) - f(a)] / (b - a);
即,拉格朗日定理是正确的。
柯西中值定理:
内容:若函数f(x), g(x)都是闭区间[a, b]的连续函数,且为开区间(a, b)可导,并且对于任意的x∈(a, b)都有g’(x) != 0,那么则有:f'(k) / g'(k) = f(b) - f(a) / g(b) - g(a);
定理证明:(还是根据罗尔中值定理)
因为涉及到导函数,所以还是想到用罗尔定理
将原式改写成:
我们即证这个等式成立即可
f'(x)[g(b) - g(a)] - g'(x)[f(b) - f(a)] = 0;
那么我们构造一个函数F'(x) = f'(x)[g(b) - g(a)] - g'(x)[f(b) - f(a)] ;
又因为带入数值有:F(a) = F(b)(可以代入自行验证)
那么就说明F(x)满足罗尔中值定理
因此F'(x) = 0;即f'(x)[g(b) - g(a)] - g'(x)[f(b) - f(a)] = 0;等式成立
那么现在证明还没完,我还要证g'(x)与[g(b) - g(a)]不等于0,那么我才能放到分母
因为g'(x) != 0是题目条件
然后我们再对g(x)函数用罗尔中值定理,因为它每一点的g'(x) != 0
因此,g(a) != g(b)不满足罗尔定理条件
所以,综上所述,g'(x)与[g(b) - g(a)]是可以放到分母位置的
再变形即为柯西中值定理了!
以上就是微分中值定理的基本内容了,接下来简要谈谈洛必达法则。
洛必达法则:
#主要内容:
若一个极限的形式为不定型极限,那么它的极限等于 (分子求导) / (分母求导)的极限。 但若(分子求导) / (分母求导)的极限不存在,原极限也可能存在。
洛必达法则是一种很方便的求不定型极限的一种方法。如果待求极限属于0/0型或∞/∞型,那么我们就可以用洛必达法则来求极限。
比如lim x->0 tanx / x这个就是一个典型的0 / 0型极限。它是可以用洛必达法则解的,极限应该为1。这里用等价无穷小可能更方便。
洛必达法则的证明这里就不证了,用到柯西中值定理。我们主要掌握其用法即可。
洛必达法则使用三项注意:
1.非不定型的极限不可使用该法则。
2.洛必达法则的条件是一个充分条件,非必要。即,如果我们求出上导/下导的极限不存在
那么也不能说明原极限不存在!这是很容易误解的一个点。此时洛必达法则是失效的
3.运用过程中可以结合讲过的等价无穷小替换等方法综合解题。
但实际情况中我们可能会碰到一些其他不定型:(基本思路,转换为基本不定型)
一、0 * ∞型:
可以将0写成1 / ∞ 或将∞写成1 / 0,进而就化为基本不定型
二、∞ - ∞型:
直接通分即可化为0 / 0型
三、0^0
指数类型:
那么一般考虑的是取对数,将指数化成乘积形式:
原理公式:a^b = e^(lna^b) = e^(b*lna);
然后指数就可以化为基本不定型了。