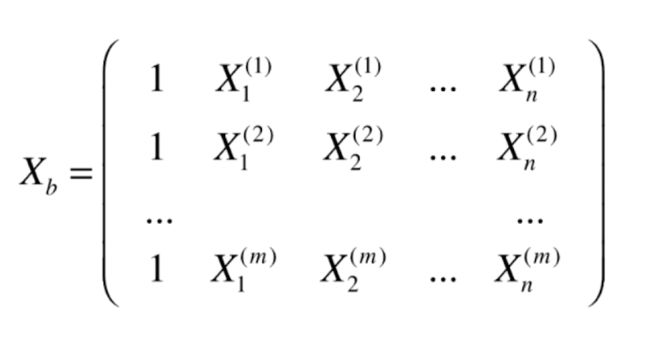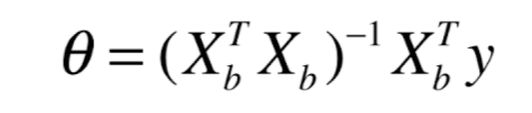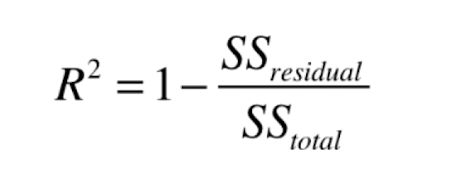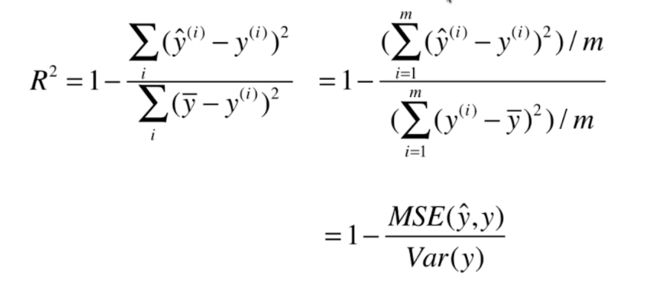线性回归算法

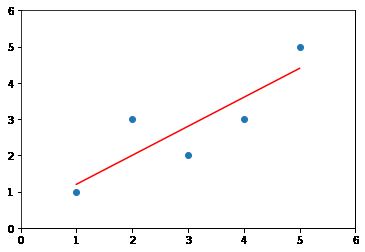
线性回归算法是寻找一条直线，最大程度的“拟合”样本与特征与样本输出标记之间的关系

线性回归算法特点：

• 解决回归问题
• 思想简单，容易实现
• 是许多强大的非线性回归模型的基础
• 结果具有良好的可解释性

实现一个简单的线性回归算法

模型的最终结果应该是对给定的数据进行拟合，形成一条直线：

y_hat⁽ⁱ⁾ = ax⁽ⁱ⁾+b

要想使得 y_hat⁽ⁱ⁾ - y⁽ⁱ⁾ 的平方和最小，经过最小二乘法计算就有：

接下来就可以通过给的数据集得出简单线性模型了。
将拟合和预测的过程进行封装：

class SimpleLinearRepression:

    def __init__(self):
        # 初始化 Simple Linear Repression 模型
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        assert x_train.ndim == 1, " Simple Linear Repression can only solve simple feature training data "
        assert len(x_train) == len(y_train), " the size of x_train must be equal to y_train "

        x_mean = x_train.mean()
        y_mean = y_train.mean()

        num = (x_train-x_mean).dot(y_train-y_mean)
        d = (x_train-x_mean).dot(x_train-x_mean)
        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self

    def predict(self, x_predict):
        # 根据给定的 x_predict 向量预测出 y_predict 向量
        assert x_predict.ndim == 1, \
            'Simple Linear Repression can only solve simple feature training data'
        assert self.a_ is not None and self.b_ is not None, \
            'must fit before predict'
        return np.array(x_predict * self.a_ + self.b_)

    def __repr__(self):
        return "SimpleLinearRepression()"

在 jupyter notebook 中使用：

x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

from python.SimpleLinearRepression import SimpleLinearRepression

slr2 = SimpleLinearRepression()

slr2.fit(x, y)

SimpleLinearRepression()

x_predict = slr2.predict(x)
x_predict

array([1.2, 2. , 2.8, 3.6, 4.4])

plt.scatter(x,y)
plt.plot(x, x_predict, color='r')
plt.axis([0,6,0,6])

这样就得到一个简单的线性模型。

多元线性回归算法

和简单的线性回归算法一样，我们应该通过拟合具有多个特征的数据得到一条直线：

然后求出theta 使得 y_hat⁽ⁱ⁾-y⁽ⁱ⁾的平方和最小。于是令：

这样就有：

最后经过矩阵运算得到（化简过程网上都有） ：

这就是多元线性回归的正规方程解（normal Equation）

• 问题：时间复杂度高
• 优点：不需要对数据进行归一化处理

实现多元线性回归模型

将算法进行封装：

import numpy as np
from sklearn.metrics import r2_score


class LinearRepression:
    def __init__(self):
        # 初始化 LinearRepression 模型
        self.interception_ = None  # 截距
        self.coef_ = None  # 系数
        self._theta = None

    def fit_normal(self, X_train, y_train):
        # 根据训练集 x_train, y_train 训练 linearRepression 模型
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def predict(self, X_predict):
        assert X_predict.shape[1] == len(self.coef_), \
            'the length of coef_ must be equal to the column of X_predict'
        assert self.coef_ is not None and self.interception_ is not None, \
            "coef_ and interception cant' be None"
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        y_predict = self.predict(X_test)
        return r2_score(y_predict, y_test)

    def __repr__(self):
        return "LinearRepression()"

在 jupyter notebook 中使用：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()

X = boston.data

y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

from python.LinearRepression import LinearRepression
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=100)

reg = LinearRepression()

reg.fit_normal(X_train, y_train)

LinearRepression()

reg.coef_

array([-1.00287922e-01,  3.26543388e-02, -4.68509409e-02,  1.02921936e+00,
       -1.15927300e+01,  3.59511341e+00, -2.53657709e-02, -1.16387369e+00,
        2.22080674e-01, -1.21981663e-02, -8.16231253e-01,  7.16938620e-03,
       -3.50243874e-01])

reg.interception_

32.20511321044348

reg.score(X_test, y_test)

0.7819244293617029

衡量线性回归算法的指标：MSE RMSE MAE 和 R Squared

其中MSE 和 RMSE 就是量纲上的差距，而 MAE 就是衡量预测值与真实值之间的平均绝对误差，思想比较简单但也很实用。
最好的线性回归评价指标 R Squared:

• R² <= 1
• R² 的值越大越好，当我们的模型不犯任何错误时得到最大值 1。
• 当我们的模型等于基准模型时， R² 取得 0。
• 如果 R² 的值 < 0 ,说明我们的模型还不如基准模型，此时很有可能我们的数据并不是线性关系。

然后让分数的分子分母同时 /m 就得到如下公式：

其中 Var(y) 就是样本数据的方差，接下来我们就来实现这些评价标准。

MSE

mse_test = np.sum((y_predict-y_test)**2) / len(y_test)
mse_test

24.156602134387438

RMSE

from math import sqrt

rmse_test = sqrt(mse_test)
rmse_test

4.914936635846635

MAE

mae_test = np.sum(np.absolute(y_predict-y_test))/len(y_test)
mae_test

3.5430974409463873

sklearn 中的MSE 和 MAE

from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error

mean_squared_error(y_test, y_predict)

24.156602134387438

mean_absolute_error(y_test, y_predict)

3.5430974409463873

R Squared

1-mean_squared_error(y_test, y_predict) / np.var(y_test)

0.6129316803937322

from sklearn.metrics import r2_score

r2_score(y_test, y_predict)

0.6129316803937324

ヾ(￣▽￣)Bye~~Bye~

个人博客：线性回归算法