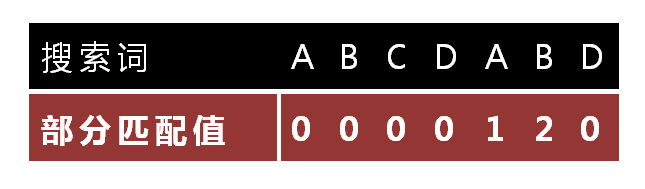KMP算法及python实现

算法思路

Knuth-Morris-Pratt（KMP）算法是解决字符串匹配问题的经典算法，下面通过一个例子来演示一下：

给定字符串"BBC ABCDAB ABCDABCDABDE"，检查里面是否包含另一个字符串"ABCDABD"。

1. 从头开始依次匹配字符，如果不匹配就跳到下一个字符

2. 直到发现匹配字符，然后经过一个内循环严查字符串是否匹配

3. 发现最后一个D不匹配，下面就该思考应该把字符串向右移动多少个位置呢？传统做法可能是移动一格，KMP算法就创新在这里。KMP算法通过查询一个Partial Match Table（表内存有字符串信息），然后计算出需要移动的步数，这个表后面会介绍怎么来的。

这里我们看到D前面是B，查表得到第二个B对应的是2，所以 移动数 = 已匹配字符数 - 查表所得数 也就是 6 - 2 = 4， 需要向右移动四格。

下面也是重复这个步骤

直到发现匹配或者字符长度超出（未发现匹配）。

Partial Match Table

那么这个查询的表是怎么来的呢？仍然以"ABCDABD"为例

－　"A"的前缀和后缀都为空集，共有元素的长度为0；

－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

python实现

def partial_table(p):
    '''''partial_table("ABCDABD") -> [0, 0, 0, 0, 1, 2, 0]'''
    prefix = set()
    res = [0]
    for i in range(1, len(p)):
        prefix.add(p[:i])
        postfix = {p[j:i + 1] for j in range(1, i + 1)}
        #print(p[:i+1],prefix,postfix,prefix & postfix or {''})
        res.append(len((prefix & postfix or {''}).pop()))
    return res

def kmp_match(s, p):
    m = len(s);
    n = len(p)
    cur = 0  # 起始指针cur
    table = partial_table(p)
    while cur <= m - n:     #只去匹配前m-n个
        for i in range(n):
            if s[i + cur] != p[i]:
                cur += max(i - table[i - 1], 1)  # 有了部分匹配表,我们不只是单纯的1位1位往右移,可以一次移动多位
                break
        else:       
            return True  # loop从 break 中退出时，else 部分不执行。
    return False

print partial_table1("ABCDABD")
print kmp_match("BBC ABCDAB ABCDABCDABDE", "ABCDABD")