冈萨雷斯Matlab版第四章(频域处理)知识点要点记录
4.1 二维离散傅里叶变换
令f(x, y)表示一幅大小为M * N的图像,其中x = 0, 1, 2, ···, M -1, y = 0, 1, 2, ···, N - 1。
- f的二维离散傅里叶变换可表示为
F(u, v),如下:

其中u = 0, 1, 2, ···, M -1, v = 0, 1, 2, ···, N - 1。频域系统时由F(u, v所张成的坐标系,其中u、v用做(频率)变量,由u = 0, 1, 2, ···, M -1, v = 0, 1, 2, ···, N - 1定义的M * N矩阵区域称为频率矩形。 - 离散傅里叶变换的逆变换为:

其中x = 0, 1, 2, ···, M -1, y = 0, 1, 2, ···, N - 1,F(u, v)的值有时称为傅里叶系数。 - 傅里叶频谱(即
F(u, v)的幅度)定义为:
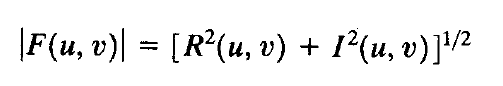
其中,R(u, v)和I(u, v)分别表示F(u, v)的实部和虚部。 - 变换的相位角定义为:

其中,R(u, v)和I(u, v)分别表示F(u, v)的实部和虚部。 - 此时,
F(u, v)又可以用复数的极坐标表示为
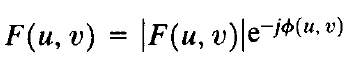
- 功率谱定义为幅度的平方,所以

- 若
f(x, y)是实数,则其傅里叶变换关于原点共轭对称,即
F(u, v) = F*(-u, -v)
其傅里叶频谱也关于原点对称
|F(u, v)| = |F(-u, -v)|
代入到F(u, v)的等式中可得
F(u, v) = F(u + M, v) = F(u, v + N) = F(u + M, v + N)
即, DFT在u和v方向上都是周期无穷的,周期由M和N决定,周期性也是DFT逆变换的一个重要属性:
f(x, y) = f(x + M, y) = f(x, y + N) = f(x + M, y + N)
即,傅里叶逆变换得到图像也是周期无穷的,DFT实现仅计算一个周期,所以我们可处理大小为M * N 的数组。
4.2 在MATLAB中计算并可视化二维DFT
-
fft2函数
一个大小为M* N的图像数组f可以通过工具箱中的函数fft2得到,简单语法为:
F = fft2(f)
该函数返回一个大小为M * N的傅里叶变换。
使用傅里叶变换进行滤波时,需要对输入数据进行零填充,此时有:
F = fft2(f, P, Q)
将所要求的0的个数对输入图像进行填充,以便结果函数的大小为P * Q。 -
abs函数
求傅里叶频谱,其语法为:
S = abs(F)
该函数计算数组的每一个元素的幅度(实部和虚部平方和的平方根)。 -
fftshift函数
将变换的原点移动到频率矩形的中心,其语法为:
Fc = fftshift(F)
其中,F是用fft2计算得到的变换,Fc是已居中的变换。函数fftshift通过变换F的象限来操作,变换计算后使用fftshift的结果与在计算变换之前将输入图像乘以(-1)x+y所得到的结果相同。注意这两种方法不能互换顺序。 -
ifftshift函数
用于颠倒这种居中,语法为:
F = ifftshift(Fc)
该函数也可以用于将最初位于矩形中心的函数变换为中心位于矩形左上角的函数。 -
floor函数
为了准确得到频率矩形的中心点位置,使用函数floor,且原点位于(1, 1)处,则MATLAB计算的频率矩形的中心点位于
[floor(M / 2) + 1, floor(N / 2) + 1]
此时,不管M和N是奇数还是偶数,计算结果总是准确的。 -
ifft函数
傅里叶逆变换函数,基本语法是:
f = ifft2(F)
其中, F是傅里叶变换,f是结果图像。由于浮点计算的舍入误差导致ifft2的输出实际上会有很小的虚数分量,所以最好在计算逆变换后提取结果的实部,以便获得仅由实数值组成的图像,语法为:
f = real(ifft2(F)); -
Tips:如果得到的频谱中值的动态范围与8比特显示(即中心处的明亮值占支配地位)相比要大得多,我们可以使用对数变换来处理,如得到频谱

此时对其做对数变换得到
S2 = log(1 + abs(Fc));

4.3 频域滤波
4.3.1 基本概念
- 空间滤波器的傅里叶变换
空间域和频域线性滤波的基础都是卷积定理,该定理可以写成:

其中,*表示两个函数的卷积,双箭头两边的表达式组成了傅里叶变换对。
第一个表达式表明,两个空间函数的卷积可以通过计算两个傅里叶变换函数的乘积的逆变换得到;相反地,两个空间函数的卷积的傅里叶变换可以由两个函数的傅里叶变换的乘积得到。
类似有第二个表达式,两个傅里叶变换函数的卷积可以通过两个空间函数的乘积的傅里叶变换得到。
对于滤波问题,我们更关注第一个表达式。空间域中的滤波由图像f(x, y)与滤波掩模h(x, y)组成,根据卷积定理,我们可以在频域中通过F(u, v) * H(u, v)得到,通常把H(u, v)称为滤波传递函数。 - 折叠误差的干扰
若周期关于函数的非零部分的持续时间很靠近,则对周期函数执行卷积运算会导致相邻周期之间的干扰,即折叠误差的干扰,可以通过补零来避免。
假设函数f(x, y)和h(x, y)的大小分别是A * B 和 C * D 。通过对f和g补零,我们构造两个大小均为P * Q的扩充的函数,可以看出,通过选择
P ≥ A + C -1
Q ≥ B + D -1
就可以避免折叠误差。 - paddedsize函数
用于计算满足前述等式的P和Q的最小偶数值。它同样提供一个选项来填充输入图像,以便形成的方形图像的大小等于最接近的2的整数次幂。FFT算法的执行时间大致取决于P和Q中的素因子的数量,在P和Q为2的整数次幂时,执行速度比Q和Q为素数时快。因此建议使用方形图像和滤波器,以便使得两个方形的滤波相同。
源码见:【MATLAB】图像处理相关函数paddedsize函数
通过使用函数paddedsize计算的PQ,我们可以使用函数fft2来计算经零填充后的FFT:
F = fft2(f, PQ(1), PQ(2));
该函数对f填充足够多的0,以便使结果图像的大小为PQ(1) * PQ(2),然后计算FFT,注意,在频域中使用填充时,滤波器的大小必须为PQ(1) * PQ(2)。
4.3.2 DFT滤波的基本步骤
若f是待滤波处理的图像,g为处理结果,同时假设滤波函数H(u, v)大小与填充后的图像的大小相等。
-
- 使用函数
paddedsize(size(f))获得填充参数
PQ = padedsize(size(f));
- 使用函数
-
- 得到使用填充的傅里叶变换:
F = fft2(f, PQ(1), PQ(2));
- 得到使用填充的傅里叶变换:
-
- 生成一个大小为PQ(1) * PQ(2)的滤波函数H。该滤波函数的格式必须是没有经过居中变换的,否则应该令
H = ifftshift(H);:
- 生成一个大小为PQ(1) * PQ(2)的滤波函数H。该滤波函数的格式必须是没有经过居中变换的,否则应该令
-
- 将该变换乘以滤波函数:
G = H .* F
- 将该变换乘以滤波函数:
-
- 获得G的傅里叶逆变换的实部:
g = real(ifft2(G));
- 获得G的傅里叶逆变换的实部:
-
- 将左上部的矩形修剪为原始大小:
g = g(1 : size(f, 1), 1 : size(f, 2));
- 将左上部的矩形修剪为原始大小:
4.3.3 用于频域滤波的M函数
- dftfilt函数
该函数可接受输入图像和一个滤波函数,可处理所有的滤波细节并输出经滤波和剪切后的图像。源码见【MATLAB】图像处理相关函数dftfilt函数
4.4 从空间滤波器获取频域滤波器
应用举例
clc
% 从空间滤波器获得频域滤波器
% FFT 傅里叶变换得到频谱
f = imread('6.png');
f = rgb2gray(f);
F = fft2(f);
S = fftshift(log(1 + abs(F)));
S = gscale(S);
figure('name', 'S'), imshow(S)
% filter 空间域的滤波器
h = fspecial('sobel')';
% figure('name', 'freqz2(h)'), freqz2(h)
% 转化为频域滤波器
PQ = paddedsize(size(f)); % 填充0之后的尺寸
H = freqz2(h, PQ(1), PQ(2)); % 频域滤波器
H1 = ifftshift(H); % dftfilt的频域滤波器是非中心化的,进行转换
% figure('name', 'abs(H)'), imshow(abs(H), [])
% figure('name', 'abs(H1)'), imshow(abs(H1), [])
% 空域滤波
gs = imfilter(double(f), h);
figure, imshow(abs(gs), [])
% 频域滤波
gf = dftfilt(f, H1);
figure, imshow(abs(gf), [])
figure, imshow(gf, [])
% creating the binary image to see the margin clearly
% 创建二值图像可以更清晰的看到边缘
figure, imshow(abs(gs) > 0.2 * abs(max(gs(:))))
figure, imshow(abs(gf) > 0.2 * abs(max(gf(:))))
4.5 在频域中直接生成滤波器
主要关注对称滤波器,即那些指定为至变换的原点的距离的各种函数的滤波器,下面我们将实现几个著名的平滑滤波器,然后介绍如何用MATLAB的线框图和表面图来可视化滤波器。
4.5.1 建立用于实现频域滤波器的网络数组
函数的核心是需要在频率矩形中计算任意点到指定点的距离函数。在MATLAB中,由于FFT的计算假设变换的原点在频率矩形的左上角,所以我们的距离计算也要用到那个点。
- dftuv函数提供距离计算及其类型应用所需要的网络数组。由函数
dftuv生成的网络数组已满足使用fft2的ifft2的处理的需要,因而无须重排数据。
源码见【MATLAB】图像处理相关函数lpfilter、dftuv函数
4.5.2 低通频域滤波器
理想低通滤波器(ILPF)具有传递函数:

其中,D0为指定的非负数,D(u,v)为点(u,v)到滤波器中心的距离。D(u,v) = D0的点的轨迹为一个圆。注意,若滤波器H乘以一幅图像的傅里叶变换,则我们会发现理想低通滤波器切断了圆外F的所有分量,而圆上和院内的点不变。
- n阶巴特沃兹低通滤波器(BLPF)(在距离原点D0处出现截止频率)的传递函数为:
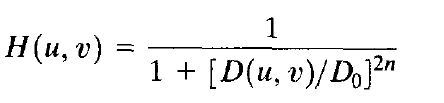
我们通常要定义一个截止频率,在该点处H(u,v)会降低为最大值的某个给定比例,当D(u, v) = D0时,H(u, v) = 0.5降为其最大值1的50%。 - 高斯低通滤波器(GLPF)的传递函数为:

其中σ为标准差,令σ = D0,我们可以根据截止参数D0得到表达式

当D(u ,v) = D0时,滤波器由最大值1降为0.607.
实现上述低通滤波器源码见【MATLAB】图像处理相关函数lpfilter、dftuv函数
4.5.3 线框图与表面图
-
mesh函数绘制线框图
语法为:mesh(H)
该函数绘制一个x = 1 : M, y = 1 : N的线框图,其中[M, N] = size(H)。若M和N很大,则线框图的密码会大到不可接受,在这种情况下,我们可以使用语法:
mesh(H(1 : k : end, 1 : k : end))
来绘制第k个点。经验表明,沿每个轴40~60个细分可在外观和分辨率之间提供较好的平衡。
MATLAB默认使用彩色绘制网线,命令
colormap([ 0 0 0])
可将线框设置为黑色。
grid on / off添加或关闭网格
axis on / off添加或关闭坐标轴
view(az, el)观察者位置为方向角az,仰角el,默认az = -37.5, e; = 30
[az, el] = view得到当前视图的几何结构
view(3)将查看点设置为默认值 -
surf函数绘制表面图
语法为:surf(H)
除了网格中的四边形用彩色填充(称为小面描影)外,该函数产生的图形与函数mesh产生的图形相同。
colormap(gray)将彩色转换为灰色
axis\grai\view与前面mesh函数用法相同
shading interp进行插值,可平滑小面描影并删除网格线 -
meshgrid函数
若目标是绘制两个变量的解析函数,则可以使用函数meshgrid函数产生坐标值,并由这些坐标值产生在mesh或surf中使用的离散矩阵。
例:绘制函数f(x, y) = x * exp(-x^2 - y^2)
[Y, X] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = X .* exp(-X .^ 2 - Y .^ 2);
mesh(Z) % Or surf(Z)
4.6 锐化频域滤波器
高通滤波通过削弱傅里叶变换的低频而保持高频相对不变,会使得图像变得更加清晰(锐化)。
4.6.1 基本高通滤波器
- hpfilter函数
给定一个低通滤波器的传递函数Hlp(u, v),通过以下语句得到高通滤波器的传递函数:
Hhp(u, v) = 1 - Hlp(u, v)
所以对函数lpfilter稍加改进就可以得到hpfilter==
源码见==【MATLAB】图像处理相关函数hpfilter函数
4.6.2 高频强调滤波
- 高频强调滤波
由于高通滤波器偏离了直流项,从而把图像的平均值降低到了零,若偏移量与将滤波器乘以一个大于1的常数结合起来,这种方法称为高频强调滤波,因为该常量乘数突出了高频部分。这个乘数也增加了低频部分的幅度,但是只要偏移量与乘数相比较小,低频增强就弱于高频增强。高频强调滤波器的传递函数为:
Hhfe(u, v) = a + b Hhp(u, v)
其中,a是偏移量,b是乘数,Hhp(u, v)是高通滤波器的传递函数。
小结
亮度变换常用于亮度缩放,空间域滤波广泛用于图像复原、彩色处理、图像分割和图像描绘子提取。