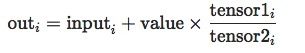PyTorch学习笔记-1.PyTorch基础概念

1.PyTorch基础概念

1.1.PyTorch简介与安装

1.1.1.PyTorch简介

2017年1月，FAIR（Facebook AI Research）发布PyTorch

PyTorch 是在Torch基础上用python语言重新打造的一款深度学习框架

Torch是采用Lua语言为接口的机器学习框架，但因Lua语言较为小众，导致Torch知名度不高

PyTorch 发展

• 2017年1月正式发布PyTorch

• 2018年4月更新0.4.0版，支持W indows系统，caffe2正式并入PyTorch

• 2018年11月更新1.0稳定版，已GitHub 增长第二快的开源项目

• 2019年5月更新1.1.0版，支持TensorBoard，增强可视化功能

• 2019年8月更新1.2.0版，更新torchvision，torchaudio 和torchtext，增加更多功能

 

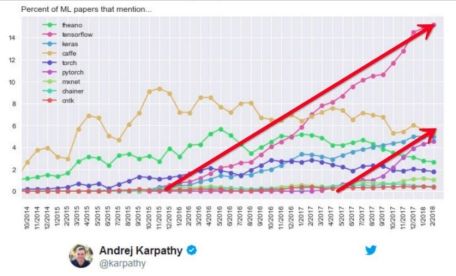
2014年1 0月至 2018年0 2月arXiv论文中深度学习框架提及次数统计，PyTorch的增长速度与TensorFlow一致

2019年3月各深度学习框架在GitHub上的Start，Forks，Watchers和Contributors数量对比

PyTorch优点

• 上手快：掌握Numpy和基本深度学习概念即可上手

• 代码简洁灵活：用nn.module封装使网络搭建更方便；基于动态图机制，更灵活

• Debug方便：调试PyTorch就像调试Python代码一样简单

• 文档规范：https://pytorch.org/docs/可查各版本文档

• 资源多：arXiv中的新算法大多有PyTorch实现

• 开发者多：GitHub上贡献者(Contributors)已超过1100+

• 背靠大树：FaceBook维护开发

•  ......

适合人群

• 深度学习初学者：模型算法实现容易，加深深度学习概念认识

• 机器学习爱好者：数十行代码便可实现人脸识别，目标检测，图像生成等有趣实验

• 算法研究员：最新arXiv论文算法快速复现

 

1.1.2.Anaconda安装

Anaconda是为方便使用python而建立的一个软件包，其包含常用的250多个工具包，多版本python解释器和强大的虚拟环境管理工具，所以Anaconda得名python全家桶

Anaconda可以使安装、运行和升级环境变得更简单，因此推荐安装使用

下载地址：https://www.anaconda.com/download/

双击下载好的安装包

选Just Me和All Users都可以

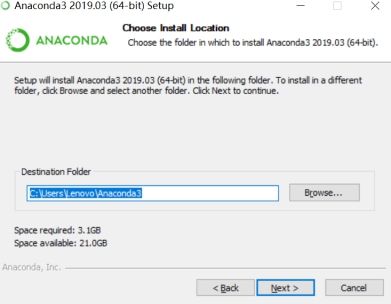
安装路径可以是默认路径，可以修改路径，只要能配置好环境即可。且路径中不要出现中文字符。

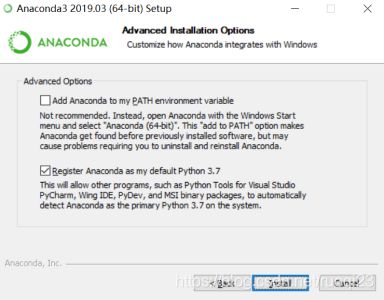
在这一步最好勾选第一个选项配置环境，也可以后续自己配置环境

验证安装成功，打开cmd，输入conda，回车

1.1.3.Pycharm安装

PyCharm 是一款功能强大的 Python 编辑器，而且可以跨平台，在macos和windows下面都可以用，这点比较好。是python现在最好用的编辑器。

PyCharm官网下载：https://www.jetbrains.com/pycharm/download/#section=windows

双击exe，进入“欢迎安装”界面，直接下一步 

2、进入“选择安装路径”界面，我一般不喜欢安装在系统盘，而是直接安装在软件下载文件夹中 ，选择好路径以后，下一步

3、 进入“安装选项”界面，按自己需求选择，全选，下一步

一直下一步，直到安装完成。

1.1.4.PyTorch安装

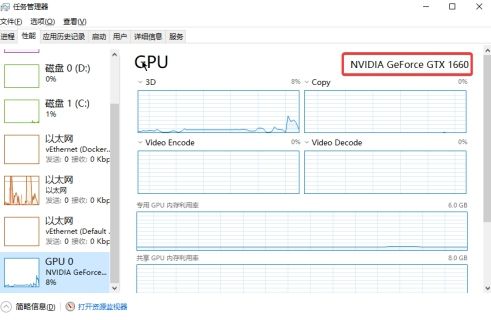
显卡配置（无 Nvidia 显卡的略过）

打开任务管理器，在GPU那里看到 NVIDIA 显卡即可。说明你的硬件驱动，已安装。

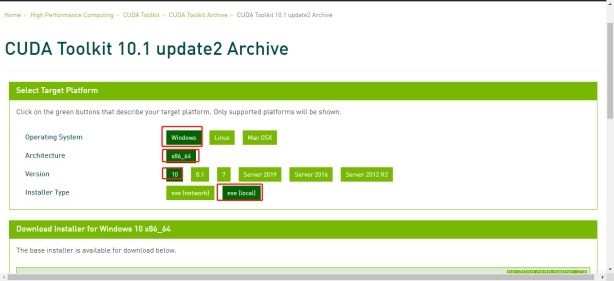
下载Cuda

官网：https://developer.nvidia.com/cuda-10.1-download-archive-update2

在https://docs.nvidia.com/cuda/cuda-toolkit-release-notes/index.html 这里可以查询到我们应该下载哪个版本

下载CuDNN 

官网 https://developer.nvidia.com/rdp/cudnn-download

安装Cuda

1.与安装其他的软件类似

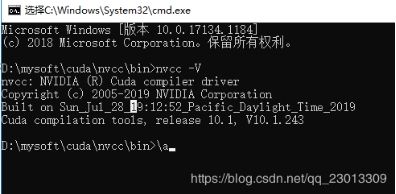
2.安装结束后将  ~/nvcc/bin(因为版本的不同可能在不同的地方) 目录添加到环境变量

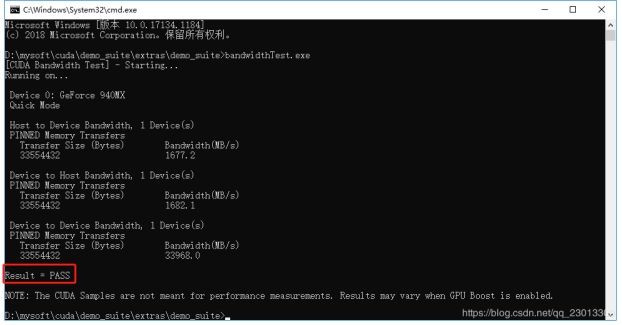
3.在命令行下输入 nvcc -V, 出现下列信息说明Cuda安装成功

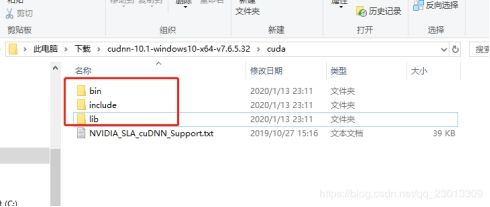
4.将CuDNN压缩包解压后，下面的三个文件夹复制到Cuda的安装目录下

5.然后执行Demo, 如果Demo中显示PASS则说明安装成功

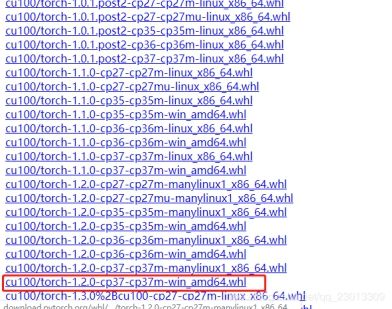
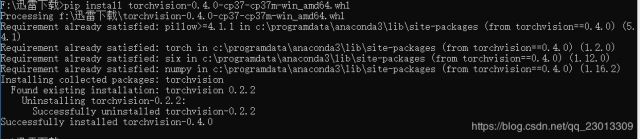
安装Pytorch

官网 https://download.pytorch.org/whl/torch_stable.html 选择合适的版本

torch/torchvision 都需要安装

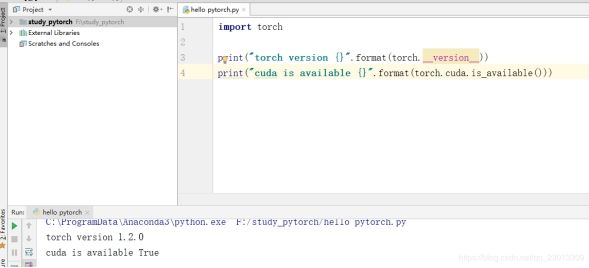
验证Pytorch

1.2.Tensor（张量）

1.2.1.张量概念 

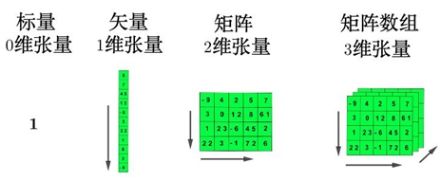
张量是一个多维数组，它是标量、向量、矩阵的高维拓展

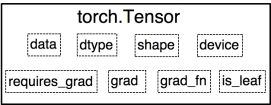
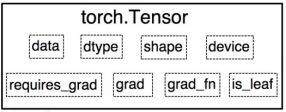
Variable是torch.autograd中的数据类型，主要用于封装Tensor，进行自动求导，其中包含的五个属性：
data:被包装的Tensor
grad:data的梯度
grad_fn:创建Tensor的Function，是自动求导的关键
requires_grad:指示是否需要梯度
is_leaf:指示是否是叶子结点（张量）

PyTorch0.4.0版开始，Variable并入Tensor
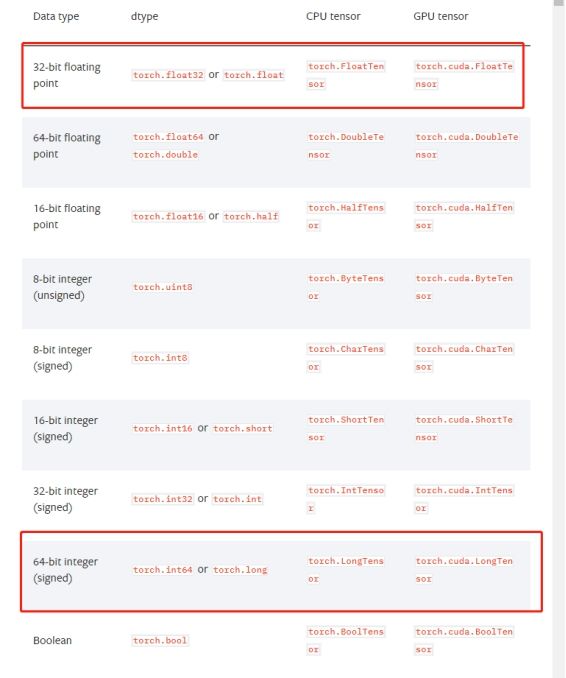
dtype:张量的数据类型，如torch.FloatTensor, torch.cuda.FloatTensor
shape:张量的形状，如(64, 3, 224, 224)
device:张量所在设备，GPU/CPU，是加速的关

PyTorch的数据类型总共有9种，常用的是float32和int64

1.2.2.直接创建张量

1.torch.tensor()：功能：从data创建tensor
• data: 数据, 可以是list, numpy
• dtype : 数据类型，默认与data的一致
• device : 所在设备, cuda/cpu
• requires_grad：是否需要梯度
• pin_memory：是否存于锁页内存，通常设置为false

torch.tensor(
data,
dtype=None,
device=None,
requires_grad=False,
pin_memory=False) 

代码实现：

# -*- coding:utf-8 -*-
import torch
import numpy as np
# 通过torch.tensor创建张量
arr = np.ones((3, 3))
print("ndarray的数据类型：", arr.dtype)
t = torch.tensor(arr, device='cuda')
# t = torch.tensor(arr)
print(t)

ndarray的数据类型： float64 tensor([[1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.]], device='cuda:0', dtype=torch.float64)

 

2.torch.from_numpy(ndarray)
功能：从numpy创建tensor
注意事项：从torch.from_numpy创建的tensor于原ndarray共享内存，当修
改其中一个的数据，另外一个也将会被改动

代码实现：

# 通过torch.from_numpy创建张量
arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)
arr[0, 0] = 0
print("numpy array: ", arr)
print("tensor : ", t)

t[0, 0] = -1
print("numpy array: ", arr)
print("tensor : ", t)

numpy array:  [[0 2 3]  [4 5 6]] tensor :  tensor([[0, 2, 3],         [4, 5, 6]], dtype=torch.int32)   修改tensor numpy array:  [[-1  2  3]  [ 4  5  6]] tensor :  tensor([[-1,  2,  3],         [ 4,  5,  6]], dtype=torch.int32)

 

1.2.3.依据数值创建张量

1 torch.zeros()
功能：依size创建全0张量
• size: 张量的形状, 如(3, 3)、(3, 224,224)
• out : 输出的张量
• layout : 内存中布局形式, 有strided,sparse_coo等
• device : 所在设备, gpu/cpu
• requires_grad：是否需要梯度

torch.zeros(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

代码实现:

# 通过torch.zeros创建张量
out_t = torch.tensor([1])

t = torch.zeros((3, 3), out=out_t)

print(t, '\n', out_t)
print(id(t), id(out_t), id(t) == id(out_t))

tensor([[0, 0, 0],         [0, 0, 0],         [0, 0, 0]])  tensor([[0, 0, 0],         [0, 0, 0],         [0, 0, 0]]) 1672654932392 1672654932392 True

 

2 torch.zeros_like()
功能：依input形状创建全0张量
• intput: 创建与input同形状的全0张量
• dtype : 数据类型
• layout : 内存中布局形式

torch.zeros_like(input,
dtype=None,
layout=None,
device=None,
requires_grad=False) 

3 torch.ones()
4 torch.ones_like()
功能：依input形状创建全1张量
• size: 张量的形状, 如(3, 3)、 (3, 224,224)
• dtype : 数据类型
• layout : 内存中布局形式
• device : 所在设备, gpu/cpu
• requires_grad：是否需要梯度

torch.ones(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False
torch.ones_like(input,
dtype=None,
layout=None,
device=None,
requires_grad=False) 

5 torch.full()
6 torch.full_like()
功能：依input形状创建全0张量
• size: 张量的形状, 如(3, 3)
• fill_value : 张量的值

torch.full(size,
fill_value,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

代码实现：

# 通过torch.full创建全1张量
t = torch.full((3, 3), 6)
print(t)

tensor([[6., 6., 6.],         [6., 6., 6.],         [6., 6., 6.]])

 

7 torch.arange()
功能：创建等差的1维张量
注意事项：数值区间为[start, end)
• start: 数列起始值
• end : 数列“结束值”
• step: 数列公差，默认为1

torch.arange(start=0,
end,
step=1,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

代码实现：

# 通过torch.arange创建等差数列张量
t = torch.arange(2, 10, 2)
print(t)

tensor([2, 4, 6, 8])

 

8 torch.linspace()
功能：创建均分的1维张量
注意事项：数值区间为[start, end]
• start: 数列起始值
• end : 数列结束值
• steps: 数列长度

torch.linspace(start,
end,
steps=100,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

代码实现：

# 通过torch.linspace创建均分数列张量
# t = torch.linspace(2, 10, 5)
t = torch.linspace(2, 10, 6)
print(t)

tensor([ 2.0000,  3.6000,  5.2000,  6.8000,  8.4000, 10.0000])

 

9 torch.logspace()
功能：创建对数均分的1维张量
注意事项：长度为steps, 底为base
• start: 数列起始值
• end : 数列结束值
• steps: 数列长度
• base : 对数函数的底，默认为10

torch.logspace(start,
end,
steps=100,
base=10.0,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

10 torch.eye()
功能：创建单位对角矩阵（ 2维张量）
注意事项：默认为方阵
• n: 矩阵行数
• m : 矩阵列数

torch.eye(n,
m=None,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

1.2.4.依概率分布创建张量

1 torch.normal()
功能：生成正态分布（高斯分布）
• mean : 均值
• std : 标准差

四种模式：
mean为标量， std为标量
mean为标量， std为张量
mean为张量， std为标量
mean为张量， std为张量

torch.normal(mean,
std,
out=None) 

代码实现：

# 通过torch.normal创建正态分布张量
# mean：张量 std: 张量
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

# mean：标量 std: 标量
t_normal = torch.normal(0., 1., size=(4,))
print(t_normal)

# mean：张量 std: 标量
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

mean:tensor([1., 2., 3., 4.]) std:tensor([1., 2., 3., 4.]) tensor([1.6614, 2.5338, 3.1850, 6.4853]) tensor([-0.4519, -0.1661, -1.5228,  0.3817]) mean:tensor([1., 2., 3., 4.]) std:1 tensor([-0.0276,  1.4369,  2.1077,  3.9417])

 

2 torch.randn()
3 torch.randn_like()
功能：生成标准正态分布
• size : 张量的形状

torch.randn(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

4 torch.rand()
5 torch.rand_like()
功能：在区间[0, 1)上，生成均匀分布

torch.rand(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

6 torch.randint()
7 torch.randint_like()
功能：区间[low, high)生成整数均匀分布
• size : 张量的形状

torch.randint(low=0,
high,
size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False) 

8 torch.randperm()
功能：生成从0到n-1的随机排列
• n : 张量的长度

torch.randperm(n,
out=None,
dtype=torch.int64,
layout=torch.strided,
device=None,
requires_grad=False) 

9 torch.bernoulli()
功能：以input为概率，生成伯努力分布（0-1分布，两点分布）
• input : 概率值

torch.bernoulli(input,
*,
generator=None,
out=None) 

1.3.张量操作与线性回归

1.3.1.张量的操作：拼接、切分、索引和变换

1.张量拼接与切分

1.1 torch.cat()
功能：将张量按维度dim进行拼接
• tensors: 张量序列
• dim : 要拼接的维度

torch.cat(tensors,
dim=0,
out=None) 

代码实现：

# -*- coding:utf-8 -*-

import torch
torch.manual_seed(1)

# torch.cat
t = torch.ones((2, 3))

t_0 = torch.cat([t, t], dim=0)
t_1 = torch.cat([t, t, t], dim=1)

print("t_0:{} shape:{}\nt_1:{} shape:{}".format(t_0, t_0.shape, t_1, t_1.shape))

t_0:tensor([[1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.]]) shape:torch.Size([4, 3]) t_1:tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],         [1., 1., 1., 1., 1., 1., 1., 1., 1.]]) shape:torch.Size([2, 9])

 

1.2 torch.stack()
功能：在新创建的维度dim上进行拼接
• tensors:张量序列
• dim :要拼接的维度

torch.stack(tensors,
dim=0,
out=None)

 代码实现：

# torch.stack
t = torch.ones((2, 3))

t_stack = torch.stack([t, t, t], dim=0)

print("\nt_stack:{} shape:{}".format(t_stack, t_stack.shape))

t_stack:tensor([[[1., 1., 1.],          [1., 1., 1.]],           [[1., 1., 1.],          [1., 1., 1.]],           [[1., 1., 1.],          [1., 1., 1.]]]) shape:torch.Size([3, 2, 3])

 

1.3 torch.chunk()
功能：将张量按维度dim进行平均切分
返回值：张量列表
注意事项：若不能整除，最后一份张量小于其他张量
• input: 要切分的张量
• chunks : 要切分的份数
• dim : 要切分的维度

torch.chunk(input,
chunks,
dim=0) 

代码实现：

# torch.chunk
a = torch.ones((2, 7))  # 7
list_of_tensors = torch.chunk(a, dim=1, chunks=3)   # 3

for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

第1个张量：tensor([[1., 1., 1.],         [1., 1., 1.]]), shape is torch.Size([2, 3]) 第2个张量：tensor([[1., 1., 1.],         [1., 1., 1.]]), shape is torch.Size([2, 3]) 第3个张量：tensor([[1.],         [1.]]), shape is torch.Size([2, 1])

 

1.4 torch.split()
功能：将张量按维度dim进行切分
返回值：张量列表
• tensor: 要切分的张量
• split_size_or_sections : 为int时，表示每一份的长度；为list时，按list 元素切分
• dim : 要切分的维度

torch.split(tensor,
split_size_or_sections,
dim=0) 

代码实现：

# torch.split
t = torch.ones((2, 5))

list_of_tensors = torch.split(t, [2, 1, 2], dim=1)  # 2
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t, t.shape))

第1个张量：tensor([[1., 1.],         [1., 1.]]), shape is torch.Size([2, 2]) 第2个张量：tensor([[1.],         [1.]]), shape is torch.Size([2, 1]) 第3个张量：tensor([[1., 1.],         [1., 1.]]), shape is torch.Size([2, 2])

 

2.张量索引

2.1 torch.index_select()
功能：在维度dim上，按index索引数据
返回值：依index索引数据拼接的张量
• input: 要索引的张量
• dim: 要索引的维度
• index : 要索引数据的序号

torch.index_select(input,
dim,
index,
out=None) 

代码实现：

# torch.index_select
t = torch.randint(0, 9, size=(3, 3))
idx = torch.tensor([0, 2], dtype=torch.long)    # float
t_select = torch.index_select(t, dim=0, index=idx)
print("t:\n{}\nt_select:\n{}".format(t, t_select))

t: tensor([[4, 5, 0],         [5, 7, 1],         [2, 5, 8]]) t_select: tensor([[4, 5, 0],         [2, 5, 8]])

 

2.2 torch.masked_select()
功能：按mask中的True进行索引
返回值：一维张量
• input: 要索引的张量
• mask: 与input同形状的布尔类型张量

torch.masked_select(input,
mask,
out=None) 

代码实现：

# torch.masked_select
t = torch.randint(0, 9, size=(3, 3))
mask = t.le(5)  # ge is mean greater than or equal/   gt: greater than  le  lt
t_select = torch.masked_select(t, mask)
print("t:\n{}\nmask:\n{}\nt_select:\n{} ".format(t, mask, t_select))

t: tensor([[4, 5, 0],         [5, 7, 1],         [2, 5, 8]]) mask: tensor([[ True,  True,  True],         [ True, False,  True],         [ True,  True, False]]) t_select: tensor([4, 5, 0, 5, 1, 2, 5])

 

3.张量变换

3.1 torch.reshape()
功能：变换张量形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存
• input: 要变换的张量
• shape: 新张量的形状

torch.reshape(input,
shape) 

代码实现：

# torch.reshape
t = torch.randperm(8)
t_reshape = torch.reshape(t, (-1, 2, 2))    # -1
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))

t[0] = 1024
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
print("t.data 内存地址:{}".format(id(t.data)))
print("t_reshape.data 内存地址:{}".format(id(t_reshape.data)))

t:tensor([5, 4, 2, 6, 7, 3, 1, 0]) t_reshape: tensor([[[5, 4],          [2, 6]],           [[7, 3],          [1, 0]]]) t:tensor([1024,    4,    2,    6,    7,    3,    1,    0]) t_reshape: tensor([[[1024,    4],          [   2,    6]],           [[   7,    3],          [   1,    0]]]) t.data 内存地址:1809503205640 t_reshape.data 内存地址:1809503205640

 

3.2 torch.transpose()
功能：交换张量的两个维度
• input: 要变换的张量
• dim0: 要交换的维度
• dim1: 要交换的维度

torch.transpose(input,
dim0,
dim1) 

代码实现：

# torch.transpose
t = torch.rand((2, 3, 4))
t_transpose = torch.transpose(t, dim0=1, dim1=2)    # c*h*w     h*w*c
print("t shape:{}\nt_transpose shape: {}".format(t.shape, t_transpose.shape))

t shape:torch.Size([2, 3, 4]) t_transpose shape: torch.Size([2, 4, 3])

3.3 torch.t()
功能： 2维张量转置，对矩阵而言，等价于torch.transpose(input, 0, 1)

torch.t(input) 

3.4 torch.squeeze()
功能： 压缩长度为1的维度（轴）
• dim: 若为None，移除所有长度为1的轴；若指定维度，当且仅当该轴长度为1 时，可以被移除；

torch.squeeze(input,
dim=None,
out=None) 

代码实现：

# torch.squeeze
t = torch.rand((1, 2, 3, 1))
t_sq = torch.squeeze(t)
t_0 = torch.squeeze(t, dim=0)
t_1 = torch.squeeze(t, dim=1)
print(t.shape)
print(t_sq.shape)
print(t_0.shape)
print(t_1.shape)

torch.Size([1, 2, 3, 1]) torch.Size([2, 3]) torch.Size([2, 3, 1]) torch.Size([1, 2, 3, 1])

 

3.5 torch.unsqueeze()
功能：依据dim扩展维度
• dim: 扩展的维度

torch.usqueeze(input,
dim,
out=None) 

1.3.2.张量数学运算

1.加减乘除

torch.add()
torch.addcdiv()
torch.addcmul()
torch.sub()
torch.div()
torch.mul() 

torch.add()
功能：逐元素计算 input+alpha×other
• input: 第一个张量
• alpha: 乘项因子
• other: 第二个张量

torch.add(input,
alpha=1,
other,
out=None) 

torch.addcdiv()

torch.addcmul()

torch.addcmul(input,
value=1,
tensor1,
tensor2,
out=None) 

代码实现：

# torch.add
t_0 = torch.randn((3, 3))
t_1 = torch.ones_like(t_0)
t_add = torch.add(t_0, 10, t_1)

print("t_0:\n{}\nt_1:\n{}\nt_add_10:\n{}".format(t_0, t_1, t_add))

t_0: tensor([[ 0.6614,  0.2669,  0.0617],         [ 0.6213, -0.4519, -0.1661],         [-1.5228,  0.3817, -1.0276]]) t_1: tensor([[1., 1., 1.],         [1., 1., 1.],         [1., 1., 1.]]) t_add_10: tensor([[10.6614, 10.2669, 10.0617],         [10.6213,  9.5481,  9.8339],         [ 8.4772, 10.3817,  8.9724]])

 

2.对数，指数，幂函数

torch.log(input, out=None)
torch.log10(input, out=None)
torch.log2(input, out=None)
torch.exp(input, out=None)
torch.pow() 

3.三角函数

torch.abs(input, out=None)
torch.acos(input, out=None)
torch.cosh(input, out=None)
torch.cos(input, out=None)
torch.asin(input, out=None)
torch.atan(input, out=None)
torch.atan2(input, other, out=None) 

1.3.3.线性回归

线性回归是分析一个变量与另外一（多）个变量之间关系的方法
因变量： y

自变量： x

关系：线性 y = wx + b
分析：求解w， b

求解步骤：
1. 确定模型 y = wx + b
2. 选择损失函数 MSE： 
3. 求解梯度并更新w,b w = w – LR * w.grad b = b – LR * w.grad

代码实现：

# -*- coding:utf-8 -*-
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)

lr = 0.05  # 学习率

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)

# 构建线性回归参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)

for iteration in range(1000):
    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

    # 清零张量的梯度
    w.grad.zero_()
    b.grad.zero_()

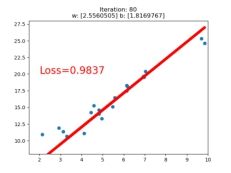
    # 绘图
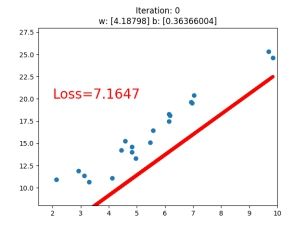
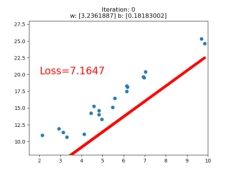
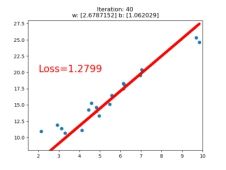
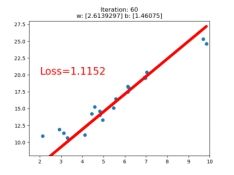
    if iteration % 20 == 0:
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)

        if loss.data.numpy() < 1:
            break

 

 

1.4.计算图与动态图机制

1.4.1.计算图

计算图是用来描述运算的有向无环图

计算图有两个主要元素： 结点（ Node）和边（ Edge）

结点表示数据，如向量，矩阵，张量
边表示运算，如加减乘除卷积等

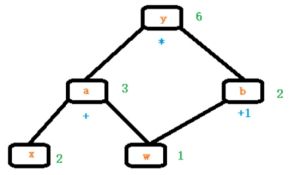
用计算图表示： y = (x+ w) * (w+1)
a = x + w b = w + 1 y = a * b

计算图与梯度求导：计算y对w的导数

=

叶子结点：用户创建的结点称为叶子结点，如X 与 W
is_leaf: 指示张量是否为叶子结点

grad_fn: 记录创建该张量时所用的方法（函数）
y.grad_fn =
a.grad_fn =
b.grad_fn =

代码实现：

# -*- coding:utf-8 -*-
import torch

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
# a.retain_grad()     # 保存a的梯度
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward()
print(w.grad)

# 查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

# 查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

# 查看 grad_fn
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

tensor([5.]) is_leaf:  True True False False False gradient:  tensor([5.]) tensor([2.]) None None None grad_fn:  None None

 

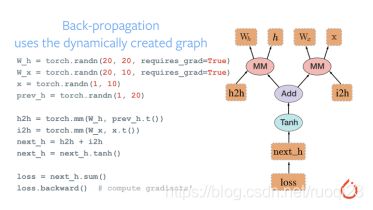
1.4.2.动态图

动态图vs 静态图

动态图 Dynamic Graph：运算与搭建同时进行，灵活，易调节  ---PyTorch

静态图：先搭建图，后运算，高效，不灵活  ---tensorflow（2.0版本之前）

1.5.自动求导与逻辑回归

1.5.1.自动求导

autograd—自动求导系统

torch.autograd.backward

功能：自动求取梯度
• tensors: 用于求导的张量，如 loss
• retain_graph : 保存计算图
• create_graph : 创建导数计算图，用于高阶求导
• grad_tensors：多梯度权重

torch.autograd.backward(tensors,
grad_tensors=None,
retain_graph=None,
create_graph=False) 

代码实现：

# -*- coding: utf-8 -*-
import torch
torch.manual_seed(10)

#retain_graph

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward(retain_graph=True)   #如果不保存，后面再次反向求导会报错
print(w.grad)
y.backward()

tensor([5.])

 

# grad_tensors
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)     # retain_grad()
b = torch.add(w, 1)

y0 = torch.mul(a, b)    # y0 = (x+w) * (w+1)
y1 = torch.add(a, b)    # y1 = (x+w) + (w+1)    dy1/dw = 2

loss = torch.cat([y0, y1], dim=0)       # [y0, y1]
grad_tensors = torch.tensor([1., 2.]) # 为y0和y1的梯度设置权重

loss.backward(gradient=grad_tensors)    # gradient 传入 torch.autograd.backward()中的grad_tensors

print(w.grad)

tensor([9.])

 

torch.autograd.grad

功能：求取梯度
• outputs: 用于求导的张量，如 loss
• inputs : 需要梯度的张量
• create_graph : 创建导数计算图，用于高阶求导
• retain_graph : 保存计算图
• grad_outputs：多梯度权重

torch.autograd.grad(outputs,
inputs,
grad_outputs=None,
retain_graph=None,
create_graph=False) 

代码实现：

# autograd.gard
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)     # y = x**2

grad_1 = torch.autograd.grad(y, x, create_graph=True)   # grad_1 = dy/dx = 2x = 2 * 3 = 6
print(grad_1)

grad_2 = torch.autograd.grad(grad_1[0], x)          # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
print(grad_2)

(tensor([6.], grad_fn=),) (tensor([2.]),)

 

autograd注意事项：
1. 梯度不自动清零

代码示例：

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b)

    y.backward()
    print(w.grad)

    w.grad.zero_()

tensor([5.]) tensor([5.]) tensor([5.]) tensor([5.])

2. 依赖于叶子结点的结点， requires_grad默认为True

代码示例：

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

print(a.requires_grad, b.requires_grad, y.requires_grad)

True True True

3. 叶子结点不可执行in-place

代码示例：

# in-place操作

a = torch.ones((1, ))
print(id(a), a)

a = a + torch.ones((1, ))
print(id(a), a)

a += torch.ones((1, ))
print(id(a), a)

1380195580808 tensor([1.]) 1380196952968 tensor([2.]) 1380196952968 tensor([3.])

 

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

w.add_(1)

y.backward()

w.add_(1) RuntimeError: a leaf Variable that requires grad has been used in an in-place operation.

 

原因是反向求导时找的是数据的地址，由于正向计算时数据是原始数据，反向求导时如果数据改变，会造成求导结果的变换，所以不允许数据的改变

1.5.2.逻辑回归

逻辑回归是线性的二分类模型
模型表达式：

称为Sigmoid函数，也称为Logistic函数，图形如下：

线性回归是分析自变量x与因变量y(标量)之间关系的方法：
逻辑回归是分析自变量x与因变量y(概率)之间关系的方法

逻辑回归也称为对数几率回归：

代码实现：

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)

# step 1/5 生成数据
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias      # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums)                         # 类别0 标签 shape=(100, 1)
x1 = torch.normal(-mean_value * n_data, 1) + bias     # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums)                          # 类别1 标签 shape=(100, 1)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)

# step 2/5 选择模型
class LR(nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x

lr_net = LR()   # 实例化逻辑回归模型

# step 3/5 选择损失函数
loss_fn = nn.BCELoss()

# step 4/5 选择优化器
lr = 0.01  # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)

# step 5/5 模型训练
for iteration in range(1000):
    # 前向传播
    y_pred = lr_net(train_x)
    # 计算 loss
    loss = loss_fn(y_pred.squeeze(), train_y)
    # 反向传播
    loss.backward()
    # 更新参数
    optimizer.step()
    # 清空梯度
    optimizer.zero_grad()
    # 绘图
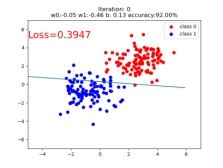
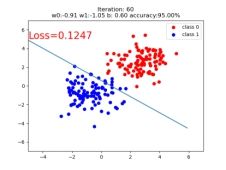
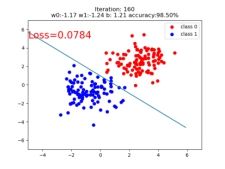
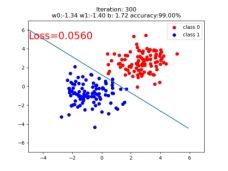
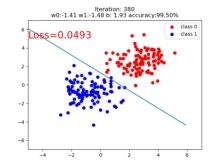
    if iteration % 20 == 0:

        mask = y_pred.ge(0.5).float().squeeze()  # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率

        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')

        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1

        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)

        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
        plt.legend()

        plt.show()
        plt.pause(0.5)

        if acc > 0.99:
            break