MATLAB的Symbolic Math Toolbox详解

---

入门

创建符号数字，变量和表达式

      下面将展示如何创建符号数字，变量和表达式。

    创建符号数字

      你可以使用sym创建符号数字。符号数字用精确的有理数表示。
      通过sym创建符号数字并与相同的浮点数对比

sym(1/3)
1/3

ans =
1/3
ans = 
	0.333

      符号结果不缩进，数值结果缩进。
      符号计算的结果是精确的，而数值计算的结果是近似的。

sin(sym(pi))
sin(pi)

ans =
0
ans =
    1.2246e-16

    创建符号变量

      你有两种方法创建符号变量，分别是syms和sym。syms是sym的简写。
      分别使用syms和sym创建符号变量x和y

syms x
y = sym('y')

      第一条命令创建了一个值为x的符号变量x。第二条命令创建了一个值为y的符号变量y。
      你可以使用syms在一条命令中创建多个变量

syms a b c

      你也可以使用sym在一条命令中创建多个变量

A = sym('a', [1 20])

A =
[a1, a2, a3, a4, a5, a6, a7, a8, a9, a10,...
a11, a12, a13, a14, a15, a16, a17, a18, a19, a20]

      当你所创建的符号变量的变量名和变量值不相同时，或者要创建符号数字时，则要使用sym。

    创建符号表达式

      黄金比例
$$\frac{1+\sqrt{5}}{2}$$
      使用下面这条命令即可用符号变量表示黄金比例

phi = (1 + sqrt(sym(5)))/2;

      你可以对phi执行各种数学运算。例如

f = phi^2 - phi - 1

f =
(5^(1/2)/2 + 1/2)^2 - 5^(1/2)/2 - 3/2

      要创建符号表达式f = phi^2 - phi - 1，首先要创建符号变量a, b, c, 和 x:

syms a b c x

      然后把表达式赋给f:

f = a*x^2 + b*x + c;

    重复使用符号对象名

      如果你设置了一个变量等于一个符号表达式，例如

syms a b
f = a + b

f = 
a + b

      接着输入

syms f

f = 
f

      MATLAB则会清除符号表达式f的值a + b。
      所以你可以使用syms命令清除原先赋给变量的值。

创建符号函数

使用syms创建自变量为x和y的函数f。创建符号函数f的同时会自动创建符号变量x和y

syms f(x,y)

把一个数学表达式赋给f

f(x,y) = x^2*y

f(x, y) =
x^2*y

找到函数f在点(3,2)的值

f(3,2)

ans =
18

符号函数同时也接受数组作为输入

xVal = 1:5;
yVal = 3:7;
f(xVal,yVal)

ans =
[ 3, 16, 45, 96, 175]

你可以对符号函数进行微分，积分，化简，用自变量本身作为输入值，和其他数学运算。例如函数f对x求导

dfx = diff(f, x)

dfx(x,y) =
2*x*y

dfx也是一个符号函数
计算df(x,y)在点x = y + 1处的值

df(y+1,y)

ans =
2*y*(y + 1)

如果你想创建常函数，比如f(x,y) = 1，你可以首先创建f(x,y)，然后再进行赋值

syms f(x,y)
f(x,y) = 1

f(x, y) =
1

如果不先创建符号函数f(x,y) 就直接进行赋值 f(x,y) = 1，则会抛出错误。

创建符号矩阵

    使用存在的符号变量

      创建一个其元素为a, b, c的循环矩阵

syms a b c
A = [a b c; c a b; b c a]

A =
[ a, b, c]
[ c, a, b]
[ b, c, a]

      计算矩阵第一行元素的和

sum(A(1, : ))

ans =
a + b + c

      使用isAlways函数，验证第一行元素之和等于第二列元素之和

isAlways(sum(A(1, : )) == sum(A( : , 2)))

ans =
  logical
   1

    创建矩阵的同时生成元素

      sym函数使你在创建符号矩阵或向量时无需提前定义元素。sym函数在创建符号矩阵的元素的同时创建矩阵。创建一个元
      素为A1_1, …, A2_4的2×4符号矩阵:

A = sym('A', [2 4])

A =
[ A1_1, A1_2, A1_3, A1_4]
[ A2_1, A2_2, A2_3, A2_4]

      可以在第一个参数中使用%d来控制矩阵元素的名字格式:

A = sym('A%d%d', [2 4])

A =
[ A11, A12, A13, A14]
[ A21, A22, A23, A24]

    创建元素为符号数字的矩阵

      sym函数的一个特别有用的功能是把数值矩阵转换为符号矩阵。
      产生一个3×3希尔伯特矩阵

A = hilb(3)

A =
    1.0000    0.5000    0.3333
    0.5000    0.3333    0.2500
    0.3333    0.2500    0.2000

      函数sym作用于A后，可得到一个精确的3×3希尔伯特符号矩阵

A = sym(A)

A =
[   1, 1/2, 1/3]
[ 1/2, 1/3, 1/4]
[ 1/3, 1/4, 1/5]

符号计算

    符号表达式的微分

      1. 单变量表达式求导
      使用函数diff对符号表达式求导:

syms x
f = sin(x)^2;
diff(f)

ans =
2*cos(x)*sin(x)

      2. 偏导数
      对于多变量符号表达式，你可以指定对哪个变量进行求导。如果你没有指定任何变量，MATLAB将选
      择距离字母x最近的变量进行求导:

syms x y
f = sin(x)^2 + cos(y)^2;

ans =
2*cos(x)*sin(x)

      符号表达式f对变量y的偏导数:

syms x y
f = sin(x)^2 + cos(y)^2;
diff(f, y)

ans =
-2*cos(y)*sin(y)

      3. 二阶偏导数和混合求导
      符号表达式f对变量y的二阶偏导数:

syms x y
f = sin(x)^2 + cos(y)^2
diff(f, y, 2)

ans =
2*sin(y)^2 - 2*cos(y)^2

      执行 diff(diff(f, y)) 可以得到相同的结果。
      混合求导:

syms x y
f = sin(x)^2 + cos(y)^2;
diff(diff(f, y), x)

ans =
0

    符号表达式的积分

      1. 单变量符号表达式的不定积分

syms x
f = sin(x)^2;
int(f)

ans =
x/2 - sin(2*x)/4

      2. 多变量符号表达式的不定积分

syms x y n
f = x^n + y^n;
int(f)

ans =
x*y^n + (x*x^n)/(n + 1)

      符号表达式f也可以对变量y进行积分:

syms x y n
f = x^n + y^n;
int(f, y)

ans =
x^n*y + (y*y^n)/(n + 1)

同理，f对变量n进行积分

syms x y n
f = x^n + y^n;
int(f, n)

ans =
x^n/log(x) + y^n/log(y)

      3. 定积分
      函数int的最后两个参数用于指定积分上下限(倒数第二个参数指定积分下限，最后一个参数指定积分
      上限)

syms x y n
f = x^n + y^n;
int(f, 1, 10)

ans =
piecewise(n == -1, log(10) + 9/y, n ~= -1,...
 (10*10^n - 1)/(n + 1) + 9*y^n)

      3. 如果MATLAB无法找到积分的闭合形式
      如果函数int无法计算出积分，它将返回一个未经处理的积分

syms x
int(sin(sinh(x)))

ans =
int(sin(sinh(x)), x)

    解方程

      1. 解一元方程
      用 == 定义一个方程

syms x
solve(x^3 - 6*x^2 == 6 - 11*x)

ans =
1
2
3

      如果不指定方程右半部分，函数solve将假定它为0:

syms x
solve(x^3 - 6*x^2 + 11*x - 6)

ans =
1
2
3

      2. 解包含多个元的方程

syms x y
solve(6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0, y)

ans =
    1
    2*x
   -3*x

如果你不指定任何变量，MATLAB将选择距离字母x最近的变量。
      3. 解方程组

syms x y z
[x, y, z] = solve(z == 4*x, x == y, z == x^2 + y^2)

x =
 0
 2
 
y =
 0
 2

z =
 0
 8

    化简符号表达式

      符号数学工具箱提供了一套化简函数供你去操作符号表达式。

phi = (1 + sqrt(sym(5)))/2;
f = phi^2 - phi - 1

f =
(5^(1/2)/2 + 1/2)^2 - 5^(1/2)/2 - 3/2

      你可以通过函数simplify化简这个答案

simplify(f)

ans =
0

      注：本小节未完待续

    符号表达式中的替换

      注：本小节未完待续

    绘制符号函数

      符号数学工具箱提供的绘图函数:
      - fplot用来在二维笛卡尔坐标系上绘制符号表达式，方程或者函数。
      - fplot3用来绘制3D图形
      - fsurf用来绘制曲面图

      1. 绘制显函数

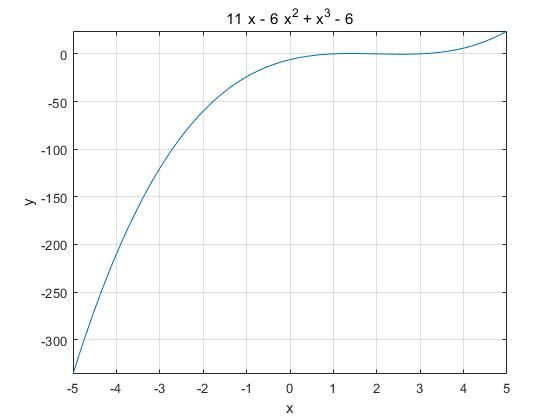
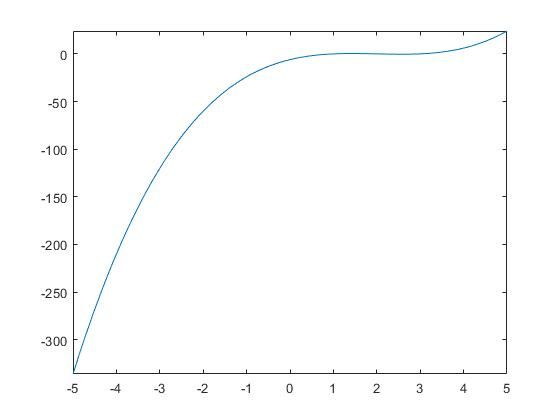
      使用fplot在二维坐标系上绘制表达式x³-6x²+11x-6

syms x
f = x^3 - 6*x^2 + 11*x - 6;
fplot(f)

      给x轴和y轴添加标签。使用texlabel(f)生成标题。使用grid on显示网格。

xlabel('x')
ylabel('y')
title(texlabel(f))
grid on

      2. 绘制隐函数

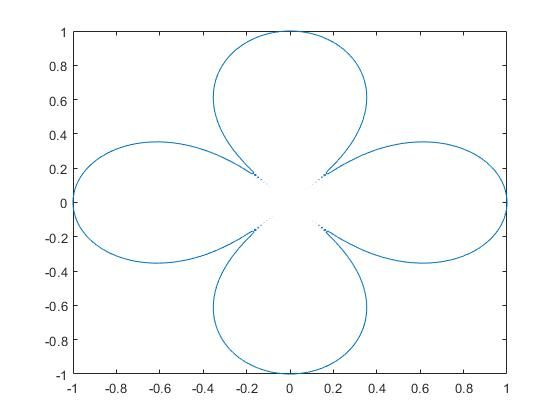
      使用fimplicit绘制方程和隐函数。
      绘制方程(x²+y²)⁴=(x²-y²)²，其中-1

syms x y
eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2;
fimplicit(eqn, [-1 1])

      3. 3D绘制
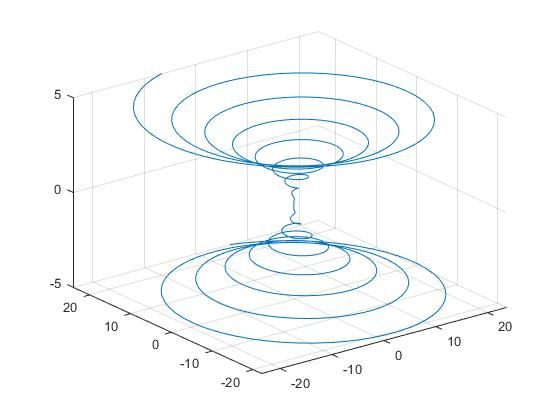
      使用fplot3绘制3D参数线。
      绘制参数线
            x = t²sin(10t)
            y = t²cos(10t)
            z = t

syms t
fplot3(t^2*sin(10*t), t^2*cos(10*t), t)

      4. 绘制曲面图
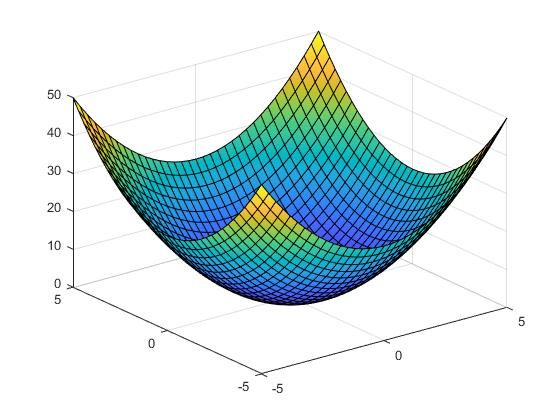
      使用fsurf绘制3D曲面图。
      绘制抛物面z = x² + y²。

syms x y
fsurf(x^2 + y^2)