- 【二分】阶乘0的数量
lamentropetion
数学数据结构
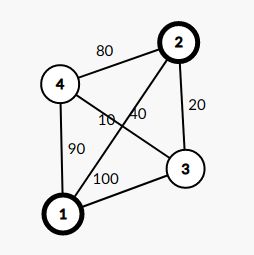
一发过!题目-阶乘0的数量V2(51nod.com)题意:思路:首先是个常识:一个数结尾0的个数取决于(2,5)这一对的个数,即5这个因子的个数然后注意特殊性,1e9个0,说明不能算出来然后n越大,阶乘里的0的个数就越多,所以满足二段性,所以可以二分统计阶乘中因子p的个数可以这样算:n/p的个数,n/(p*p)的个数....这样加起来就好了Code:#include#defineintlonglo
- 51Nod1011 最大公约数GCD(C语言)
BuffaloBit
算法训练01-大学训练ACMc语言
输入2个正整数A,B,求A与B的最大公约数。Input2个数A,B,中间用空格隔开。(1intgcd(inta,intb){return(b>0)?gcd(b,a%b):a;}intmain(){inta,b;while(scanf("%d%d",&a,&b)!=EOF)printf("%d\n",gcd(a,b));return0;}最大公约数就是最大公因数,指两个或多个整数中共有的因数中最大的
- 51nod 冲刺题
Alaso_shuang
OJ选择OI新手入门刷题c++算法蓝桥杯
进阶习题:http://www.51nod.com/Question/Index.html#questionId=1481数数字http://www.51nod.com/Challenge/Problem.html#problemId=2151队列复原https://www.51nod.com/Challenge/Problem.html#problemId=3593小明的数字表vector-ST
- K8s初次入门
城市的五彩
k8s
初步:搭建k8s集群k8s集群主机清单主机名ip地址master1.50node-00011.51node-00021.52node-00031.53node-00041.54node-00051.55harbor1.30事先准备所有的k8s集群主机卸载防火墙和禁用swap交换空间(docker、k8s建议禁用swap)安装工具dnfinstall-ykubeadmkubeletkubectlco
- [51Nod]1013 3的幂的和
闭门造折
很有代表性的一道题,用到了快速幂和逆元题干求:3^0+3^1+...+3^(N)mod1000000007快速幂参考资料《基础算法—快速幂详解》快速幂的原理是,计算m^k次方的时候,通过k的二进制值将k拆分成2^i+2^j+...,通过不断地平方运算快速计算m的k次方逆元这个真是个奇妙的东西以1013题为例,整个证明过程如下:原式=[1-3^(n+1)]/(1-3)=[3^(n+1)-1]/2[1
- dfs_全排列 51Nod - 1384
Cherish_lii
dfsdfs全排列51Nod-1384
题目:给出一个字符串S(可能有重复的字符),按照字典序从小到大,输出S包括的字符组成的所有排列。例如:S="1312",输出为:112311321213123113121321211321312311311231213211Input输入一个字符串S(S的长度#include#includeusingnamespacestd;charin[300],b[300],out[300];//输入标记输出
- 51nod 1241:特殊的排序
2997ms
好玩51nod
1241特殊的排序题目来源:摩根斯坦利的比赛题基准时间限制:1秒空间限制:131072KB分值:80难度:5级算法题收藏关注一个数组的元素为1至N的整数,现在要对这个数组进行排序,在排序时只能将元素放在数组的头部或尾部,问至少需要移动多少个数字,才能完成整个排序过程?例如:25341将1移到头部=>12534将5移到尾部=>12345这样就排好了,移动了2个元素。给出一个1-N的排列,输出完成排序
- 最长公共子序列(LCS)
亦往沧劫
最长公共子序列LCS最长公共子序列
来源:https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1006一些概念:(1)子序列:一个序列A=a1,a2,……an,中任意删除若干项,剩余的序列叫做A的一个子序列。也可以认为是从序列A按原顺序保留任意若干项得到的序列。例如:对序列1,3,5,4,2,6,8,7来说,序列3,4,8,7是它的一个子序列。对于一个长度为n
- 51Nod 2152 数字组合 c/c++题解
东瓜lqd
#51Nod51Nod算法题解dfs
题目描述现在小瓜有1到n这n个整数,他想知道用这n个整数组成一个长度为n的数字序列的所有方法(每个整数可以重复使用)。你能帮助他吗?输入一行一个整数n(1#include#include#include#include#include#include#include#include#include#include#include#include#include#include#include#in
- 【51nod】二进制统计【位运算】
VL——MOESR
题解题解c++51nod位运算
思路:直接lowbit判断即可codecodecode#include#includeusingnamespacestd;intt;inta[32];intmain(){scanf("%d",&t);while(t--){intx,tot=0;scanf("%d",&x);x=x&(-x);x>>=1;while(x){x>>=1;tot++;}a[tot]++;}for(inti=0;i<=31
- 51nod 1629 B君的圆锥
纯真zwj
小学几何题
1629B君的圆锥基准时间限制:1秒空间限制:131072KB分值:10难度:2级算法题收藏关注B君要用一个表面积为S的圆锥将白山云包起来。B君希望包住的白山云体积尽量大,B君想知道体积最大可以是多少。注意圆锥的表面积包括底面和侧面。Input一行一个整数,表示表面积S。(1 #include#include#includeusingnamespacestd;constdoublepi=4.0*a
- 51Nod - 1629 B君的圆锥
メイ
51Nod-1629B君的圆锥B君要用一个表面积为S的圆锥将白山云包起来。B君希望包住的白山云体积尽量大,B君想知道体积最大可以是多少。注意圆锥的表面积包括底面和侧面。Input一行一个整数,表示表面积S。(1 #include#includeusingnamespacestd;constdoublePI=3.14159265358979;inlinedoublefun(doublex,const
- 51Nod 1629 B君的圆锥 c/c++题解
东瓜lqd
#51Nod51Nod算法题解计算几何简单数学
题目描述:B君要用一个表面积为S的圆锥将白山云包起来。B君希望包住的白山云体积尽量大,B君想知道体积最大可以是多少。注意圆锥的表面积包括底面和侧面。输入一行一个整数,表示表面积S。(1#include#include#include#include#include#include#include#include#include#include#include#include#include#inc
- 【三分】51nod 1629 B君的圆锥
CN_swords
搜索
51nod1629B君的圆锥(三分)/*time:2016/12/2write:Swords题意:给你一个圆锥的表面积大小,让你求这样表面积的圆锥体积最大是多少题解:三分法根据选半径确定最大体积,r的范围不大于10^5(因为S不大于10^9)。*/#include#include#include#definePI3.1415926535898#defineeps1e-7usingnamespace
- 51Nod-1629-B君的圆锥
f_zyj
计算几何数学相关51Nod-题解集锦计算几何
ACM模版描述题解已知圆锥的面积S,求最大体积V的公式为:V=S*sqrt(S/(72*Pi))。代码#include#include#include#definePI3.1415926usingnamespacestd;intmain(){ints;cin>>s;doubleres=s*sqrt(s/(72.0*PI));printf("%f\n",res);return0;}参考《计算几何相关
- linux cont配置svn,idea右键没有svn选项
weixin_42399342
linuxcont配置svn
StackPanel在增加控件的问题今天遇到这样一个问题,就是我做了一个自定义控件.然后加到StackPanel中,[51nod1685]第k大区间Description定义一个长度为奇数的区间的值为其所包含的的元素的中位数.现给出$n$个数,求将所有长度为奇数的区间的值排序后,第$k$大的值为多少.Input第一行两个数$n$和$k$....hdu_3555
- 51Nod 1092 回文字符串 c/c++题解
东瓜lqd
#51Nod51Nod算法题解区间DPLCS
题目描述回文串是指aba、abba、cccbccc、aaaa这种左右对称的字符串。每个字符串都可以通过向中间添加一些字符,使之变为回文字符串。例如:abbc添加2个字符可以变为acbbca,也可以添加3个变为abbcbba。方案1只需要添加2个字符,是所有方案中添加字符数量最少的。输入输入一个字符串Str,Str的长度#include#include#include#include#include
- 各大刷题网站OJ
没头脑特高兴
刷题链接http://poj.org/pojhttp://www.spoj.com/spojhttp://acm.hdu.edu.cn/hduhttps://cn.vjudge.net/vj(包含大部分网站的题库)http://www.51nod.com51Nod(算法较强,过了能看别人的代码)http://acm.zju.edu.cnzojhttp://acm.csu.edu.cn/Online
- NOIP刷题网站系统noipoj
区块in
杂事
刷题链接http://noipoj.cnNOIPOJ在线评测系统http://poj.org/pojhttp://www.spoj.com/spojhttp://acm.hdu.edu.cn/hduhttps://cn.vjudge.net/vj(包含大部分网站的题库)http://www.51nod.com51Nod(算法较强,过了能看别人的代码)http://acm.zju.edu.cnzoj
- 刷题链接
weixin_30699463
php
刷题链接http://poj.org/pojhttp://acm.hdu.edu.cn/hduhttp://acm.hust.edu.cn/vjudgevj(基本包含其它网站的题库)http://www.51nod.com51Nod(算法较强)http://acm.zju.edu.cnzojhttp://acm.csu.edu.cn/OnlineJudge/csuhttp://acm.hrbust
- 各大刷题站点
qupeng110
随笔
刷题链接http://poj.org/pojhttp://www.spoj.com/spojhttp://acm.hdu.edu.cn/hduhttps://cn.vjudge.net/vj(包含大部分网站的题库)http://www.51nod.com51Nod(算法较强,过了能看别人的代码)http://acm.zju.edu.cnzojhttp://acm.csu.edu.cn/Online
- 51nod1287 加农炮 构造顺序序列 二分查找
克莱蛙
二分
说出来你可能不信,今天又被秀了。1287加农炮题目来源:Codility一个长度为M的正整数数组A,表示从左向右的地形高度。测试一种加农炮,炮弹平行于地面从左向右飞行,高度为H,如果某处地形的高度大于等于炮弹飞行的高度H(A[i]>=H),炮弹会被挡住并落在i-1处,则A[i-1]+1。如果H所有的A[i],这个炮弹也无效。现在给定N个整数的数组B代表炮弹高度,计算出最后地形的样子。例如:地形高度
- 图论 —— 环与块
Alex_McAvoy
——————图论——————#图论——环与块
【概述】在图论中,环与块的问题十分常见,包括求最小环、判负环、DAG图判定、求图中是否存在环、求连通块等最小环:点击这里负权环:点击这里连通块的计数:点击这里DAG图判定:点击这里【例题】Wormholes(POJ-3259)(Ford判负环):点击这里CurrencyExchange(POJ-1860)(Ford求递增环):点击这里DAG图判定(51Nod-2143)(DAG图判定):点击这里两
- WC2018 游记
weixin_33894640
数据结构与算法
第一次写游记。。。[day0]第一次去长沙,可能也是最后一次,5h火车坐的真难受,更难受的是还要去什么荒郊野岭比赛,一副离wc三连跪不远的节奏。接站大巴上讨论了一波51nod的E,听说现在出了一种新的筛法,常数吊打洲鸽筛,我两天前才学的洲鸽筛。。。进了宿舍发现宿舍没有网(其实是宿舍玻璃太nb,把信号全屏蔽了),不过外面的wifi信号还是蛮好评(毕竟能容纳600多人,网速还有100+k)。去了一趟家
- 路径记录(很久之前)
weixin_33681778
数据结构与算法c/c++
已弃坑。12.22【BZOJ】2243[SDOI2011]染色树链剖分+线段树【BZOJ】1724[Usaco2006Nov]FenceRepair切割木板手写堆【BZOJ】1455罗马游戏左偏树【BZOJ】1202:[HNOI2005]狡猾的商人【BZOJ】1270[BeijingWc2008]雷涛的小猫1.18【51NOD】1201整数划分动态规划(经典)【51NOD】1096距离之和最小数学
- 贪心算法之区间相关小结
风之旅人c
选择不相交问题问题描述:数轴上有n个开区间(ai,bi),尽量选择多个区间,是的这些区间两两之间没有共同点。例题51Nod1133https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1133题目分析将所有的线段按照终点升序,起点降序的顺序进行排列。贪心策略是:选择第一个线段,之后每次选择不相交的线段,凡是相交或者是覆盖的线段
- 公开游戏、基于有向图的游戏
csuzhucong
chrome前端
目录〇,背景一,公开游戏、策梅洛定理1,公开游戏2,策梅洛定理二,有向图游戏1,狭义有向图游戏2,广义有向图游戏3,狭义有向图游戏的SG数4,BashGame力扣292.Nim游戏(正向Bash)51Nod1066Bash游戏(正向Bash)51Nod1067Bash游戏V2(正向拓展Bash)51Nod1068Bash游戏V3(正向拓展Bash)三,公平游戏、公平组合游戏、Sprague-Gru
- 【欧拉函数】最大公约数之和
lamentropetion
数学算法c++数据结构
感觉就是欧拉函数裸题啊ez捏问题-最大公约数之和(51nod.com)题意:思路:枚举i肯定超时考虑枚举gcd那就是去枚举n的因子p然后根据题意推一推式子就出来了!Code:#include#defineintlonglongusingnamespacestd;intn;intphi(intx){vector>v;intres=x;for(inti=2;i1)v.push_back({x,1});
- 51nod1040&poj 2480(欧拉函数-最大公约数)1-n同n的最大公约数之和
阿启呀
数论数论欧拉函数最大公约数
题目给出一个n,求1-n这n个整数,同n的最大公约数的和。比如:n=6;1,2,3,4,5,6同6的最大公约数分别为1,2,3,2,1,6,加在一起=15。输入1个整数N(N#includeusingnamespacestd;#definelllonglonglleuler(llx){llres=x;for(inti=2;i*i1)res=res/x*(x-1);returnres;}intmai
- CentOS 7部署k8s集群(v1.19.16)
一般等价物(污妖王)
k8skubernetescentoslinux
一、安装k8s1.1、安装环境dockerv19.03.15Centos8安装docker_centos8安装docker_一般等价物(污妖王)的博客-CSDN博客节点IP主机名master192.168.110.251test251node1192.168.110.252test252node2192.168.110.253test253--------------------以下步骤所有机器都
- Dom
周华华
JavaScripthtml
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- 【Spark九十六】RDD API之combineByKey
bit1129
spark
1. combineByKey函数的运行机制
RDD提供了很多针对元素类型为(K,V)的API,这些API封装在PairRDDFunctions类中,通过Scala隐式转换使用。这些API实现上是借助于combineByKey实现的。combineByKey函数本身也是RDD开放给Spark开发人员使用的API之一
首先看一下combineByKey的方法说明:
- msyql设置密码报错:ERROR 1372 (HY000): 解决方法详解
daizj
mysql设置密码
MySql给用户设置权限同时指定访问密码时,会提示如下错误:
ERROR 1372 (HY000): Password hash should be a 41-digit hexadecimal number;
问题原因:你输入的密码是明文。不允许这么输入。
解决办法:用select password('你想输入的密码');查询出你的密码对应的字符串,
然后
- 路漫漫其修远兮 吾将上下而求索
周凡杨
学习 思索
王国维在他的《人间词话》中曾经概括了为学的三种境界古今之成大事业、大学问者,罔不经过三种之境界。“昨夜西风凋碧树。独上高楼,望尽天涯路。”此第一境界也。“衣带渐宽终不悔,为伊消得人憔悴。”此第二境界也。“众里寻他千百度,蓦然回首,那人却在灯火阑珊处。”此第三境界也。学习技术,这也是你必须经历的三种境界。第一层境界是说,学习的路是漫漫的,你必须做好充分的思想准备,如果半途而废还不如不要开始。这里,注
- Hadoop(二)对话单的操作
朱辉辉33
hadoop
Debug:
1、
A = LOAD '/user/hue/task.txt' USING PigStorage(' ')
AS (col1,col2,col3);
DUMP A;
//输出结果前几行示例:
(>ggsnPDPRecord(21),,)
(-->recordType(0),,)
(-->networkInitiation(1),,)
- web报表工具FineReport常用函数的用法总结(日期和时间函数)
老A不折腾
finereport报表工具web开发
web报表工具FineReport常用函数的用法总结(日期和时间函数)
说明:凡函数中以日期作为参数因子的,其中日期的形式都必须是yy/mm/dd。而且必须用英文环境下双引号(" ")引用。
DATE
DATE(year,month,day):返回一个表示某一特定日期的系列数。
Year:代表年,可为一到四位数。
Month:代表月份。
- c++ 宏定义中的##操作符
墙头上一根草
C++
#与##在宏定义中的--宏展开 #include <stdio.h> #define f(a,b) a##b #define g(a) #a #define h(a) g(a) int main() { &nbs
- 分析Spring源代码之,DI的实现
aijuans
springDI现源代码
(转)
分析Spring源代码之,DI的实现
2012/1/3 by tony
接着上次的讲,以下这个sample
[java]
view plain
copy
print
- for循环的进化
alxw4616
JavaScript
// for循环的进化
// 菜鸟
for (var i = 0; i < Things.length ; i++) {
// Things[i]
}
// 老鸟
for (var i = 0, len = Things.length; i < len; i++) {
// Things[i]
}
// 大师
for (var i = Things.le
- 网络编程Socket和ServerSocket简单的使用
百合不是茶
网络编程基础IP地址端口
网络编程;TCP/IP协议
网络:实现计算机之间的信息共享,数据资源的交换
协议:数据交换需要遵守的一种协议,按照约定的数据格式等写出去
端口:用于计算机之间的通信
每运行一个程序,系统会分配一个编号给该程序,作为和外界交换数据的唯一标识
0~65535
查看被使用的
- JDK1.5 生产消费者
bijian1013
javathread生产消费者java多线程
ArrayBlockingQueue:
一个由数组支持的有界阻塞队列。此队列按 FIFO(先进先出)原则对元素进行排序。队列的头部 是在队列中存在时间最长的元素。队列的尾部 是在队列中存在时间最短的元素。新元素插入到队列的尾部,队列检索操作则是从队列头部开始获得元素。
ArrayBlockingQueue的常用方法:
- JAVA版身份证获取性别、出生日期及年龄
bijian1013
java性别出生日期年龄
工作中需要根据身份证获取性别、出生日期及年龄,且要还要支持15位长度的身份证号码,网上搜索了一下,经过测试好像多少存在点问题,干脆自已写一个。
CertificateNo.java
package com.bijian.study;
import java.util.Calendar;
import
- 【Java范型六】范型与枚举
bit1129
java
首先,枚举类型的定义不能带有类型参数,所以,不能把枚举类型定义为范型枚举类,例如下面的枚举类定义是有编译错的
public enum EnumGenerics<T> { //编译错,提示枚举不能带有范型参数
OK, ERROR;
public <T> T get(T type) {
return null;
- 【Nginx五】Nginx常用日志格式含义
bit1129
nginx
1. log_format
1.1 log_format指令用于指定日志的格式,格式:
log_format name(格式名称) type(格式样式)
1.2 如下是一个常用的Nginx日志格式:
log_format main '[$time_local]|$request_time|$status|$body_bytes
- Lua 语言 15 分钟快速入门
ronin47
lua 基础
-
-
单行注释
-
-
[[
[多行注释]
-
-
]]
-
-
-
-
-
-
-
-
-
-
-
1.
变量 & 控制流
-
-
-
-
-
-
-
-
-
-
num
=
23
-
-
数字都是双精度
str
=
'aspythonstring'
- java-35.求一个矩阵中最大的二维矩阵 ( 元素和最大 )
bylijinnan
java
the idea is from:
http://blog.csdn.net/zhanxinhang/article/details/6731134
public class MaxSubMatrix {
/**see http://blog.csdn.net/zhanxinhang/article/details/6731134
* Q35
求一个矩阵中最大的二维
- mongoDB文档型数据库特点
开窍的石头
mongoDB文档型数据库特点
MongoDD: 文档型数据库存储的是Bson文档-->json的二进制
特点:内部是执行引擎是js解释器,把文档转成Bson结构,在查询时转换成js对象。
mongoDB传统型数据库对比
传统类型数据库:结构化数据,定好了表结构后每一个内容符合表结构的。也就是说每一行每一列的数据都是一样的
文档型数据库:不用定好数据结构,
- [毕业季节]欢迎广大毕业生加入JAVA程序员的行列
comsci
java
一年一度的毕业季来临了。。。。。。。。
正在投简历的学弟学妹们。。。如果觉得学校推荐的单位和公司不适合自己的兴趣和专业,可以考虑来我们软件行业,做一名职业程序员。。。
软件行业的开发工具中,对初学者最友好的就是JAVA语言了,网络上不仅仅有大量的
- PHP操作Excel – PHPExcel 基本用法详解
cuiyadll
PHPExcel
导出excel属性设置//Include classrequire_once('Classes/PHPExcel.php');require_once('Classes/PHPExcel/Writer/Excel2007.php');$objPHPExcel = new PHPExcel();//Set properties 设置文件属性$objPHPExcel->getProperties
- IBM Webshpere MQ Client User Issue (MCAUSER)
darrenzhu
IBMjmsuserMQMCAUSER
IBM MQ JMS Client去连接远端MQ Server的时候,需要提供User和Password吗?
答案是根据情况而定,取决于所定义的Channel里面的属性Message channel agent user identifier (MCAUSER)的设置。
http://stackoverflow.com/questions/20209429/how-mca-user-i
- 网线的接法
dcj3sjt126com
一、PC连HUB (直连线)A端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 二、PC连PC (交叉线)A端:(568A): 白绿,绿,白橙,蓝,白蓝,橙,白棕,棕; B端:(标准568B):白橙,橙,白绿,蓝,白蓝,绿,白棕,棕。 三、HUB连HUB&nb
- Vimium插件让键盘党像操作Vim一样操作Chrome
dcj3sjt126com
chromevim
什么是键盘党?
键盘党是指尽可能将所有电脑操作用键盘来完成,而不去动鼠标的人。鼠标应该说是新手们的最爱,很直观,指哪点哪,很听话!不过常常使用电脑的人,如果一直使用鼠标的话,手会发酸,因为操作鼠标的时候,手臂不是在一个自然的状态,臂肌会处于绷紧状态。而使用键盘则双手是放松状态,只有手指在动。而且尽量少的从鼠标移动到键盘来回操作,也省不少事。
在chrome里安装 vimium 插件
- MongoDB查询(2)——数组查询[六]
eksliang
mongodbMongoDB查询数组
MongoDB查询数组
转载请出自出处:http://eksliang.iteye.com/blog/2177292 一、概述
MongoDB查询数组与查询标量值是一样的,例如,有一个水果列表,如下所示:
> db.food.find()
{ "_id" : "001", "fruits" : [ "苹
- cordova读写文件(1)
gundumw100
JavaScriptCordova
使用cordova可以很方便的在手机sdcard中读写文件。
首先需要安装cordova插件:file
命令为:
cordova plugin add org.apache.cordova.file
然后就可以读写文件了,这里我先是写入一个文件,具体的JS代码为:
var datas=null;//datas need write
var directory=&
- HTML5 FormData 进行文件jquery ajax 上传 到又拍云
ileson
jqueryAjaxhtml5FormData
html5 新东西:FormData 可以提交二进制数据。
页面test.html
<!DOCTYPE>
<html>
<head>
<title> formdata file jquery ajax upload</title>
</head>
<body>
<
- swift appearanceWhenContainedIn:(version1.2 xcode6.4)
啸笑天
version
swift1.2中没有oc中对应的方法:
+ (instancetype)appearanceWhenContainedIn:(Class <UIAppearanceContainer>)ContainerClass, ... NS_REQUIRES_NIL_TERMINATION;
解决方法:
在swift项目中新建oc类如下:
#import &
- java实现SMTP邮件服务器
macroli
java编程
电子邮件传递可以由多种协议来实现。目前,在Internet 网上最流行的三种电子邮件协议是SMTP、POP3 和 IMAP,下面分别简单介绍。
◆ SMTP 协议
简单邮件传输协议(Simple Mail Transfer Protocol,SMTP)是一个运行在TCP/IP之上的协议,用它发送和接收电子邮件。SMTP 服务器在默认端口25上监听。SMTP客户使用一组简单的、基于文本的
- mongodb group by having where 查询sql
qiaolevip
每天进步一点点学习永无止境mongo纵观千象
SELECT cust_id,
SUM(price) as total
FROM orders
WHERE status = 'A'
GROUP BY cust_id
HAVING total > 250
db.orders.aggregate( [
{ $match: { status: 'A' } },
{
$group: {
- Struts2 Pojo(六)
Luob.
POJOstrust2
注意:附件中有完整案例
1.采用POJO对象的方法进行赋值和传值
2.web配置
<?xml version="1.0" encoding="UTF-8"?>
<web-app version="2.5"
xmlns="http://java.sun.com/xml/ns/javaee&q
- struts2步骤
wuai
struts
1、添加jar包
2、在web.xml中配置过滤器
<filter>
<filter-name>struts2</filter-name>
<filter-class>org.apache.st