论文阅读——椭圆检测算法 2015 A fast and robust ellipse detector based on top-down least-square fitting

    今天阅读了一个2015年的一篇论文，关于椭圆检测的，向作者发送邮件索取代码和原始数据也没回我- -||。所以只阅读文章思想并从算法上分析其性能。下面开始对文章进行分析。

〇 摘要部分

现存的算法通常使用一个自下而上的策略（bottom-up strategy）将边缘点或者椭圆弧段组合为椭圆，因此限制了其鲁棒性。作者提出了一个快速准确的椭圆检测算法，算法的主要思想是利用一种新的自上而下的拟合策略（top-down fitting strategy）来将边缘点组合为椭圆，并使用积分链（integral chain）来加速拟合过程。

阅读到这里，心里存了三个疑问，在后面的阅读中，带着这些疑问进行阅读：

① bottom-up strategy 是什么，是如何应用在椭圆检测中的；

② top-down fitting strategy 是什么，作者如何使用这个进行椭圆检测，它为什么比bottom-up strategy要好；

③ integral chain是什么，是如何进行加速拟合过程的，这个加速是有损加速还是无损加速。

一 介绍

（介绍部分我这里就不全部翻译了，只列出对写论文和了解其他算法有用的说明。）

    椭圆检测的应用：交通标志识别，汽车安全性的增强，广播体育视频的矫正（这里我理解为跟踪足球类运动），细胞检测与计数。

    下面是关于椭圆检测的发展：

    （1）基于霍夫变换（HT）的。标准HT算法最明显的问题就是因其5维参数，占用巨大的内存，为了克服这个问题，有两种可能的解决办法：

    一个可能的方法就是在投票过程中，使用边缘点的子集，不是使用全部边缘点。例如：随机霍夫变换（RHT），概率霍夫变换（PHT），模糊霍夫变换（FHT）均基于这个思想。

     另一个可能的方法就是将五维空间分解为具有较小维数的子空间来降低标准HT的时间和空间复杂度。例如：迭代随机霍夫变换（IRHT）使用五个1维加速器来替代原始5维的加速器。Chia等人在几何上计算4个参数，并使用一个1维加速器来计算最后一个参数。

    （2）基于启发式的。比如基于遗传算法（GA）和多群体遗传算法的（MPGA），这些算法可以得到比较好的结果，但是有找到次优解的可能。（个人认为，基于启发式的算法更像是将椭圆检测这个问题抽象出一个目标函数，使用这些工具进行自动求解。事实上，椭圆是一个具有多种几何性质的一个图形，如果想使用启发式的算法，可以结合深度学习考虑下。）

    （3）基于边缘连接的。上述的两类算法耗时严重，无法达到实时性。现在比较热门的且达到实时性的算法是基于这样的框架：先根据边缘点的几何性质构造椭圆弧段或者区域，然后使用拟合算法得到椭圆参数。典型的有三个算法进行说明（论文对这三个算法的总结我认为有点一般，所以下面是加入了自己的理解）：

     Prasad等人的椭圆检测算法（2012）：Canny边缘检测 → 使用直线段去逼近边缘段 → 使用曲率和凸性分割出椭圆弧段 → 构造弧段的搜索区域来组合可能属于同一个椭圆的弧段 → 拟合椭圆获得最后的结果。

    Patraucean等人的椭圆检测算法（2012）：算法名称叫ELSD，实际上是直线段和椭圆弧段检测算法，目的是检测出直线段和椭圆弧段，不能算是完整的椭圆检测算法，毕竟没有椭圆弧段合并过程。思想与Prasad的类似，只不过边缘检测实现的方式不一样，是基于Sobel+区域生长来获得的。然后根据几何性质分割出直线段和椭圆段，并使用NFA来剔除错误直线段和椭圆弧段（NFA我认为是个创新点）。

    Fornaciari等人的椭圆检测算法（2014）：这个文章是将边缘分割为4类弧段，每类弧段在一个象限内，然后在不同象限内进行组合。细节部分可以看文章，我认为这个作者是发现了椭圆检测的核心问题，椭圆弧段的组合，所以他得到了很好的结果。椭圆检测的精度直接受到组合算法的影响，而拟合算法间接的影响检测时间。

    介绍完椭圆检测的基本发展，下面对这个论文的算法进行进一步分析。

二 背景

    背景部分主要介绍椭圆的拟合方法和候选椭圆的选择。

    椭圆拟合是对下面这个公式进行拟合，在拟合之前对数据进行0均值处理，就是防止拟合时候4次方项对数据精度造成影响（一定要注意，很严重）。

    拟合之后采用下述的方法来判断是否是真实椭圆。pi是每个像素点的坐标，就是每个像素点带入拟合方程，如果拟合误差很大，这个像素被抛弃，最后统计有效像素点与全体像素点的比值，小于0.7则认为这个拟合出的椭圆是虚假椭圆，扔掉。

三 提出的算法

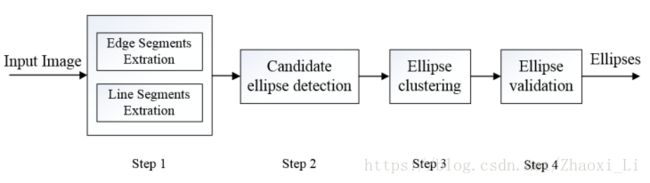
     算法的流程图如下图所示，是属于基于边缘链接的方法。下面对每个过程进行分析。

1 边缘段提取

    首先进行高斯模糊 → 计算自适应Canny阈值 → Canny边缘检测得到边缘图像。对于每个像素，如果其梯度大于计算出的高阈值，认为去是强边缘点（strong edge point），在高低阈值之间的叫做弱边缘点（weak edge point）。然后从边缘图中提取出一条条的边缘线，提取方法就是从强边缘点开始进行8邻域搜索，直到搜索不出可连接的点为止。然后重新选择一个强边缘点作为起点进行新的搜索。简而言之，边缘段提取就是提取出图像的边缘线。

2 直线段提取

    简单来说，就是从边缘段的尾部开始，计算尾部到直线的这段边缘段是否能够构成直线，如果不能就从尾部的前一个点开始一样的判定。说白了，就是使用一系列直线段去逼近这个边缘段。

3 使用top-down方案选择边缘段

    在这个小节，作者给出了bottom-up strategy的含义。

Bottom-up strategy iteratively fits line segments or arcs into ellipses from shorter ones to longer ones. 

    以直线段逼近为例，bottom-up是从第2个像素开始，如果其是直线，那么再从第三个点开始，直到其不满足直线条件，作者top-down就是完全反过来的过程。同理在这个小节中，在获得一组直线段之后，作者想从这里获得椭圆，思想很简单，以下图为例，先拟合直线段1~9，看其是否能够构成一个椭圆，如果不能，那么就从其中的一个子集进行拟合，直到有满足条件的椭圆拟合出来。拟合成功之后，剔除参与拟合的直线段。再对剩下的进行相同的操作。

-----------------------

到这里，前面的两个问题已经能够理解了，在进行直线段选择时候，如果选择bottom-up的思想，很容易提前终止，即椭圆的一部分参与拟合，过早结束。但我觉得无论是bottom-up还是top-down，都具有其特色，记住其思想，针对具体问题具体分析。

bottom-up 从小不断扩充到大，直到扩充的点不满足约束。

top-down 从大不断得到到小，直到选择的子集满足约束。

------------------------

4 使用积分链加速

    上述说的top-down方法非常耗时，这里使用积分图像技术中的1维情况（被称为integral chain）进行加速提出的椭圆检测算法。这个我觉得不是什么重点，算是个小创新。

    椭圆拟合时候涉及到大量重复计算，这个是针对其算法做的一个优化计算的方法。算是一种无损加速，这里不细分析了。

5 椭圆聚类

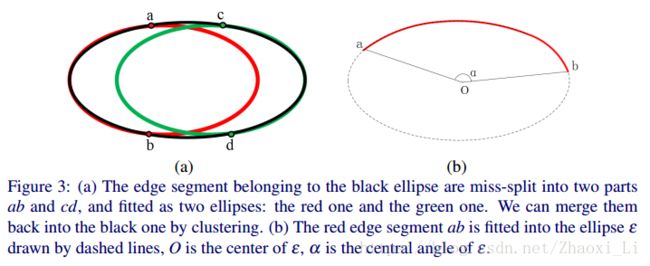
    一个完整的椭圆收到噪声影响会被分割成多个弧段，一个椭圆可能会产生两个候选椭圆。组合方式也很简单，计算每个椭圆的参与拟合的直线段对应的张角，然后进行排序，选择一个椭圆，然后在从剩下的中找到可能组合的椭圆，然后两个在一起拟合一次，如果拟合结果更好，则合并这两个椭圆。重复以上过程，最终得到一系列椭圆。

6 椭圆验证

    椭圆验证就是基于ELSD中的NFA剔除错误结果的思想的进一步改进。关于改进NFA思想是否有效的问题，我需要进一部分分析，从作者的改进说明上来看，其动机不是很明显。有机会我自己实现下分析其创新性。

    经过以上6步，算法最终会产生一组椭圆。这就是算法的全部。

四 实验部分

    作者采用的是Fornaciari和ELSD的算法进行对比（这两个对比算法作者已经提供了源代码，这个作者就不提供，我好气啊）。验证准则很好理解，阅读论文自然就能明白，这里不细说。椭圆的数据集都是公开的，3个数据集一个是Prasad的，一个是随机图像数据集，一个是手机拍出的序列图像数据集。都有ground-truth标记。下图是作者的结果。

下图是作者在这三个数据集整体的结果，有一定的进步。

    作者的创新点看似比较简单，我觉得其内部应该有很多细节没有注意到，有时间的话，我自己复现下作者的代码，验证下之前自己的想法。而且在阅读椭圆检测论文时候，同一个代码，同一个数据集，跑出的F-measure值都不一样，很奇怪，在后续研究中我得把这个问题想明白了。

    这篇文章没有源码，不明白的地方或者有独特见解的欢迎讨论。

British Machine Vision Conference