数学知识--Methods for Non-Linear Least Squares Problems（第二章）

Methods for Non-Linear Least Squares Problems 非线性最小二乘问题的方法
2nd Edition, April 2004
K. Madsen, H.B. Nielsen, O. Tingleff

2 Descent Methods
第二章 下降方法

非线性优化的所有方法都是 iterative：从一个起始点 x0 开始，算法生成一系列向量 x1 , x2 ,…, 这些点我们希望其收敛到一个 局部极小值点 x* 对于给定函数，大多数算法强加了一个 the descending condition

这就阻止了向局部极大值收敛，同时减少了向 saddle point 收敛的可能性。如果给定一个函数具有多个极小值解，那么结果将依赖于起始点位置。我们不知道哪个极小值解能够发找到，它和起始点的距离无关。

在大多数情况下，算法生成的向量在向局部极小值点收敛的过程存在两个完全不同的阶段。当起始点 x0 距离极小值很远的时候，我们希望算法通过迭代能够稳定向 局部极小值x移动。在这个“全局阶段”的每一步迭代，我们要求误差变小

在最后的迭代阶段，当xk 距离 x很近时，我们希望更快的收敛。常用的三种收敛定义如下：


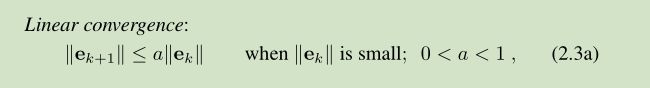
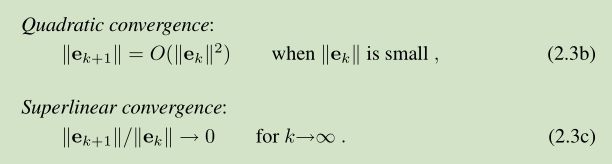
一个 descent method 每一步迭代过程主要包括两点：1）找到一个下降方向 hd （ descent direction hd ），2）寻找一个步长 step length ，可以是 函数值产生一个好的减少量。a good decrease in the F-value

假定 x 为 函数 F 上的一个点，还有一个半直线，起点为 x ,直线方向为 h。现在我们来分析一下 F 沿着这个半直线其函数值的变化情况。泰勒展开如下：

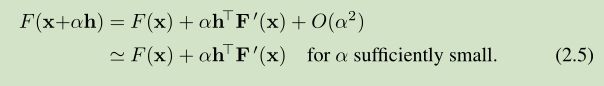
如果 F(x+αh) 在 α=0处 是一个关于 α 的下降函数，那么我们称 h 是一个 下降方向。

这里我们需要结合 descending condition 公式（2.1）的定义来看。
F(x+αh) - F(x) < 0

如果没有这样的 h 存在，那么 F’(x)=0，那么 x 就是一个 stationary。否则我们需要选择一个步长 α （我们沿着 hd 方向 走多远），这样我们就得到目标函数值得一个下降量。寻找步长的一种方法如下（一个近似）

这个过程叫 line search 线性搜索。 接下来我们首先介绍下降方向的两个方法。 two methods for computing a descent direction

2.1. The Steepest Descent method
根据公式（2.5）我们推导得到如下公式

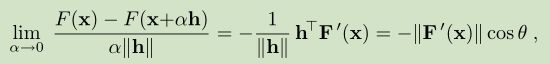
θ 是 向量 h 和 F’(x) 的夹角。
上面公式显示 当 θ=π 我们得到最大下降量，即我们使用最大下降方向 hsd = -F’(x)
基于 公式（2.8）的方法称之为 最大梯度下降方法 steepest descent method or gradient method。

最大梯度下降方法在 迭代初期收敛效果很好，但是在迭代后期因为 linear 所以 很慢。
如何解决这个问题了？使用组合算法，就是结合两个算法的优势。在初期使用 如 gradient method ，在后期使用另一种算法 如 Newton’s method。hybrid method 一个主要问题就是 两种算法在何时切换比较好。

2.2. Newton’s Method
下面我们来推导牛顿算法，假定 x* 是一个 stationary point，根据 Definition 1.6 ，它满足 F’(x)=0， 从泰勒展开看，这是一个非线性方程系统。


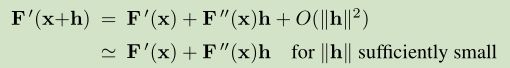
找到 一个 hn 作为公式（2.9a）的解。
假定 H 是正定矩阵，那么它是 非奇异的。对所有 非零 u，u’Hu>0 。 对（2.9a）两边同时乘以 hn 的转置

上面公式显示 hn 是一个下降方向：它满足 Definition 2.6 的条件。

当 x 距离 x* 很近时，Newton’s method 在迭代后期表现很好。我们可以发现（see Frandsen et al (2004)）当 在solution位置 的 Hessian 是正定的，当我们位于 x* 附近区域的某个位置，其 F’’(x) 是正定的，我们得到 quadratic convergence。

我们可以结合 Newton’s method and the steepest descent method 得到一个 hybrid method

但是上面的方法不实用，因为需要计算 F’’(x) ，这对于复杂系统是不现实的。我们可以使用 Quasi-Newton method 来逼近 H*= F’’(x*), 后面我们会介绍该方法。

2.3. Line Search
给定点 x, 一个下降方向 descent direction h，下一步迭代就是从 x 开始 沿着 h 前进一步。为了找到这一步有多大，我们分析在 x 和 h 邻域 给定函数值得变化

因为 h 是一个 descent direction，根据 Definition 2.6. Descent direction 所以满足

这就表明 当 α 足够小，我们满足（2.1）的 descending condition，也就是

通常在使用 Newton’s method，我们给 α 一个初始值如 α=1

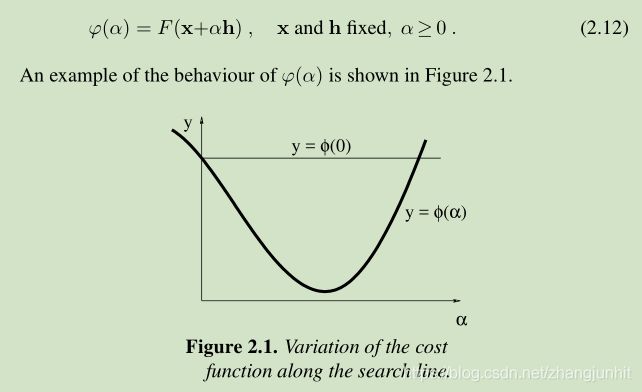
Figure 2.1 描述了三种不同的情形

ϕ(α)≥ϕ(0) 对应上图中的哪里了？ ϕ(0) 两个交点的右交点的右侧

exact line search 是一个迭代过程，产生一系列点 α1 ,α2 …。目标就是找到 公式（2.7）的 true minimizer αe， 当 αs 满足
where τ is a small, positive number
迭代过程中我们使用下面的计算值来近似 ϕ(α)的变化

exact line search 比较浪费时间：当 x 离 x较远时，搜索方向 h 可能离 x-x 很远， 这时就没必要很准确的计算出 ϕ 的最小真值。这也是提出 soft line search 的背景。我们接受一个 α-value，只要它不属于 上面列的第一种第二种情况就可以了。

If the starting guess on α satisfies both these criteria, then we accept it as αs

2.4. Trust Region and Damped Methods
假定我们用一个模型 L 来表示 函数 F 在 当前迭代位置 x 的邻域 的 behaviour

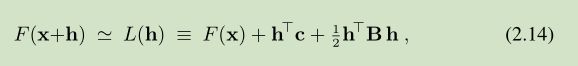
对于一个 trust region method 来说，我们假定知道一个 正数 ∆，这个模型 L 在 一个球内足够准确， ball with radius ∆, centered at x
determine the step as

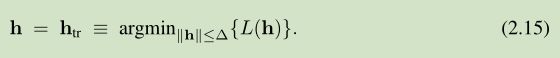
对于 damped method 来说， the step is determined as

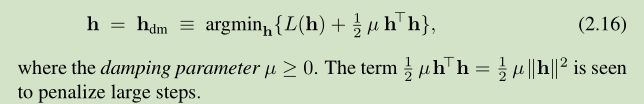
Algorithm 2.4 核心部分基于上面两种方法的实现形式如下：

当 h 足够小时， L(h) 被认为可以对 F(x+h) 进行很好的近似。步长计算失败的原因就是 h 太大，应该被减小。如果 一个步长被接受，在下一步迭代中我们应该用一个更大的步长，以便减少迭代步数尽快收敛到 x *。

这里我们定义一个 gain ratio 来评估 计算步长的模型的质量

对于一个 trust region method 我们通过控制半径 ∆ 的大小来监测 step length，下面的更新策略被广泛应用。

a damped method 一个 更新策略广泛应用如下所示：

还有一个比上面更好的更新策略

2.4.1. Computation of the step
对于一个 a damped method 来说，其 步长 step 的计算作为下面函数的一个 stationary point


a damped method and a trust region method ：the two classes of methods are closely related, but there is not a simple formula for the connection between the ∆- and µ-values that give the same step.

11