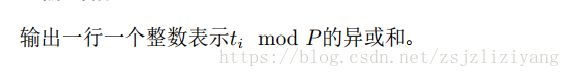100035. 【NOIP2017提高A组模拟7.10】区间

Description

Input

Output

Sample Input

sample1:
4 2 10
5 1 1 10
sample2:
1000 97 96998351
41 1668 505 2333

Sample Output

sample1:
4
sample2:
1749769

Data Constraint

Solution

对于20%的数据可以 n2 n 2 暴力，对于70%的数据可以用线段树维护区间的乘积。然后每次询问i~i+k-1的乘积，再求答案。

Code1

#include 
#include
#include
#include
#define N 2000010
#define ll long long
using namespace std;
int n,k,p,a,b,c,d;
ll s[N],tree[N*13],ans,st=1;
void build(int l,int r,int x){
    if(l==r){
        tree[x]=s[l];
        return;
    }
    int mid=(l+r)/2;
    build(l,mid,x*2);
    build(mid+1,r,x*2+1);
    tree[x]=(tree[x*2]*tree[x*2+1])%p;
}
void find(int s,int t,int l,int r,int x){
    if(s==l&&t==r){
        st=(st*tree[x])%p;
        return;
    }
    int mid=(l+r)/2;
    if(t<=mid) find(s,t,l,mid,x*2);
    else if(s>mid) find(s,t,mid+1,r,x*2+1);
    else{
        find(s,mid,l,mid,x*2);
        find(mid+1,t,mid+1,r,x*2+1);
    } 
}
int main(){
    freopen("range.in","r",stdin);
    freopen("range.out","w",stdout);
    scanf("%d%d%d",&n,&k,&p);
    scanf("%d%d%d%d",&a,&b,&c,&d);
    s[1]=a;
    for(int i=2;i<=n;i++) s[i]=(s[i-1]*b+c)%d;
    build(1,n,1);
    for(int i=1;i<=n-k+1;i++){
        find(i,i+k-1,1,n,1);
        ans=(ans xor st);
        st=1;
    }
    printf("%lld\n",ans);
    return 0;
}

对于100%的数据其实并没有用那么高级的数据结构，只是分块一下，k个一块，然后对于每一块维护前缀积和后缀积，每个长度为k的区间对应了一整块区间或者前一块的后缀和前一块的前缀，然后直接乘起来就好了。时间复杂度O(n)。

Code2

#include 
#include
#include
#define N 20000010
#define ll long long
using namespace std;
ll a,b,c,d,n,k,p;
int f[N],g[N],s[N],ans;
int main(){
    freopen("range.in","r",stdin);
    freopen("range.out","w",stdout);
    scanf("%lld%lld%lld",&n,&k,&p);
    scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
    s[1]=a;
    for(int i=2;i<=n;i++){
        ll x=((ll)s[i-1]*b+c)%d;
        s[i]=(int)x;
    }
    for(int i=1;i<=n;i++){
        if(i%k==1){
            ll x=(ll)s[i]%p;
            f[i]=(int)x;
        }
        else{
            ll x=((ll)f[i-1]*(ll)s[i])%p;
            f[i]=(int)x;
        }
    }
    for(int i=n;i>=1;i--){
        if(i%k==0){
            ll x=(ll)s[i]%p;
            g[i]=(int)x;
        }
        else{
            ll x=((ll)g[i+1]*(ll)s[i])%p; 
            g[i]=(int)x;
        }
    }
    for(int i=1;i<=n-k+1;i++){
        if(i%k==1){
            ll x=((ll)f[i+k-1])%p;
            ans^=(int)x;
        }
        else{
            ll x=((ll)g[i]*(ll)f[i+k-1])%p;
            ans^=(int)x;
        }
    }
    printf("%d\n",ans);
    return 0;
}

注意类型的转换，这里有点坑。

---

作者：zsjzliziyang
QQ:1634151125
转载及修改请注明
本文地址:https://blog.csdn.net/zsjzliziyang/article/details/81545176