走马观花之《视觉SLAM十四讲》

1. 视觉SLAM 系统概述

SLAM 是Simultaneous Localization and Mapping 的缩写，中文译作“同时定位与地图构建” 。它是指搭载特定传感器的主体，在没有环境先验信息的情况下，于运动过程中建立环境的模型，同时估计自己的运动。如果这里的传感器主要为相机，那就称为“视觉SLAM”。

视觉SLAM流程分为以下几步

• 传感器信息读取。在视觉SLAM 中主要为相机图像信息的读取和预处理。
• 视觉里程计。视觉里程计任务是估算相邻图像间相机的运动，以及局部地图的样子。
• 后端优化。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。
• 回环检测。回环检测判断机器人是否曾经到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。
• 建图。它根据估计的轨迹，建立与任务要求对应的地图。

2. 前端视觉里程计

视觉里程计根据相邻图像的信息，估计出粗略的相机运动，给后端提供较好的初始值。视觉里程计的算法主要分为两个大类：特征点法和直接法。基于特征点法的前端，长久以来（直到现在）被认为是视觉里程计的主流方法。它运行稳定，对光照、动态物体不敏感，是目前比较成熟的解决方案。
核心问题：如何根据图像估计相机运动。

2.1. 特征点法

特征点：由关键点和描述子两部分组成。关键点是指该特征点在图像里的位置，有些特征点还具有朝向、大小等信息。描述子通常是一个向量，按照某种人为设计的方式，描述了该关键点周围像素的信息。描述子是按照“外观相似的特征应该有相似的描述子”的原则设计的。

特征匹配：视觉SLAM 中极为关键的一步，特征匹配解决了SLAM 中的数据关联问题，即确定当前看到的路标与之前看到的路标之间的对应关系。通过对图像与图像，或者图像与地图之间的描述子进行准确的匹配，我们可以为后续的姿态估计，优化等操作减轻大量负担。匹配方法：暴力匹配等。

当相机为单目时，我们只知道2D 的像素坐标，因而问题是根据两组2D 点估计运动。该问题用对极几何来解决。

当相机为双目、RGB-D 时，或者我们通过某种方法得到了距离信息，那问题就是根据两组3D 点估计运动。该问题通常用ICP 来解决。

如果我们有3D 点和它们在相机的投影位置，也能估计相机的运动。该问题通过PnP求解。

2.1.1. 2D-2D: 对极几何

假设我们从两张图像中，得到了一对配对好的特征点，如果我们有若干对这样的匹配点，就可以通过这些二维图像点的对应关系，恢复出在两帧之间摄像机的运动。


八点法+奇异值分解即可求得旋转矩阵R和位移向量t。

2.1.2. 三角测量

在得到运动之后，下一步我们需要用相机的运动估计特征点的空间位置。在单目SLAM 中，仅通过单张图像无法获得像素的深度信息，我们需要通过三角测量（Triangulation）（或三角化）的方法来估计地图点的深度。

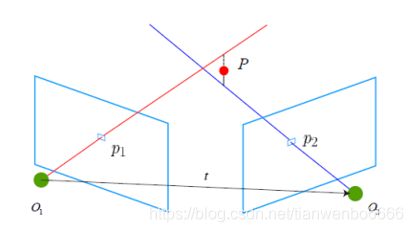
2.1.3. 3D-2D: PnP

PnP（Perspective-n-Point）是求解3D 到2D 点对运动的方法。它描述了当我们知道n 个3D 空间点以及它们的投影位置时，如何估计相机所在的位姿

如果两张图像中，其中一张特征点的3D 位置已知，那么最少只需三个点对（需要至少一个额外点验证结果）就可以估计相机运动

在双目或RGB-D 的视觉里程计中，我们可以直接使用PnP 估计相机运动。而在单目视觉里程计中，必须先进行初始化，然后才能使用PnP

PnP 问题有很多种求解方法，例如用三对点估计位姿的P3P，直接线性变换（DLT），非线性优化构建最小二乘问题并迭代求解

2.1.4. 3D-3D: ICP

假设一组配对好的3D 点（比如对两个RGB-D 图像进行了匹配）：

现在，找一个欧氏变换R; t，使得：

这个问题可以用迭代最近点（Iterative Closest Point, ICP）求解
ICP 的求解也分为两种方式：利用线性代数的求解（主要是SVD），以及利用非线性优化方式的求解（类似于Bundle Adjustment）。

2.1.5. 特征点法的缺陷

特征点法存在的问题：

• 关键点的提取与描述子的计算非常耗时
• 使用特征点时，忽略了除特征点以外的所有信息。一张图像有几十万个像素，而特征点只有几百个。只使用特征点丢弃了大部分可能有用的图像信息。
• 相机有时会运动到特征缺失的地方，往往这些地方没有明显的纹理信息。
  克服对策：
• 只计算关键点，不计算描述子。同时，使用光流法（Optical Flow）来跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间，而光流本身的计算时间要小于特征点的计算与匹配。
• 只计算关键点，不计算描述子。同时，使用直接法（Direct Method）来计算特征点在下一时刻图像的位置。这同样可以跳过描述子的计算过程，而且直接法的计算更加简单。

2.2. 光流法

光流法仍然使用特征点，只是把匹配描述子替换成了光流跟踪，估计相机运动时仍使用对极几何、PnP 或ICP 算法。

光流是一种描述像素随着时间，在图像之间运动的方法，计算部分像素运动的称为稀疏光流，计算所有像素的称为稠密光流。

LK光流是光流法的一种，它对观测量做了“灰度不变”假设和“某个窗口内的像素具有相同的运动”假设。因而能够从前后两幅图片中追踪到同一个点的位置移动。

在实际应用中，LK光流的作用就是跟踪特征点。与对每一帧提取特征点相比，使用LK光流只需要提取一次特征点，后续视频帧只需要跟踪就可以了，节约了许多特征提取时间。

2.3. 直接法

在直接法中，根据图像的像素灰度信息同时估计相机的运动和点的投影，不要求提取到的点必须为角点。


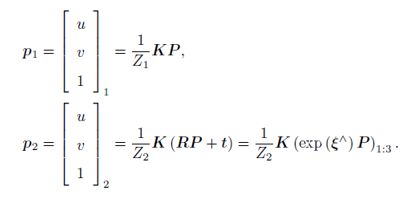
直接法的思路是根据当前相机的位姿估计值，来寻找p2 的位置。但若相机位姿不够好，p2 的外观和p1 会有明显差别。于是，为了减小这个差别，我们优化相机的位姿，来寻找与p1 更相似的p2。光度误差（Photometric Error），也就是P 的两个像的亮度误差：

优化目标为该误差的二范数

能够做这种优化的理由，仍是基于灰度不变假设。在直接法中，假设一个空间点在各个视角下，成像的灰度是不变的。有许多个（比如N 个）空间点Pi，那么，整个相机位姿估计问题变为：

然后使用G-N 或L-M 计算增量，迭代求解。

3. 后端优化

前端视觉里程计能给出一个短时间内的轨迹和地图，但由于不可避免的误差累积，这个地图在长时间内是不准确的。所以，在视觉里程计的基础上，我们还希望构建一个尺度、规模更大的优化问题，以考虑长时间内的最优轨迹和地图。

3.1. 线性系统和卡尔曼滤波KF

3.2. 非线性系统和扩展的卡尔曼滤波EKF

把卡尔曼滤波器的结果拓展到非线性系统中来，称为扩展卡尔曼滤波器（ExtendedKalman Filter，EKF）。通常的做法是，在某个点附近考虑运动方程以及观测方程的一阶泰勒展开，只保留一阶项，即线性的部分，然后按照线性系统进行推导。

先定义一个卡尔曼增益Kk：

在卡尔曼增益的基础上，后验概率的形式为：

3.3. 光束法平差BA

所谓的Bundle Adjustment，是指从视觉重建中提炼出最优的3D 模型和相机参数（内参数和外参数）。从每一个特征点反射出来的几束光线（bundles of light rays），在我们把相机姿态和特征点空间位置做出最优的调整(adjustment) 之后，最后收束到相机光心的这个过程，简称为BA。

左侧的p 是全局坐标系下的三维坐标点，右侧的us， vs 是该点在图像平面上的最终像素坐标。
系统的观测方程为：

z=h(T,p)

其中，T为相机的位姿变换矩阵,其对应的李代数为ξ。
则以最小二乘的角度考虑，可得此次观测的误差：

e=z-h(T,p)

然后，把其他时刻的观测量也考虑进来，我们可以给误差添加一个下标。设zij 为在位姿ξi 处观察路标pj 产生的数据，那么整体的代价函数（Cost Function）为：

对这个最小二乘进行求解，相当于对位姿和路标同时作了调整，也就是所谓的BA。

3.4. 位姿图优化

构建一个只有轨迹的图优化，而位姿节点之间的边，可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。一旦初始估计完成，我们就不再优化那些路标点的位置，而只关心所有的相机位姿之间的联系了。通过这种方式，我们省去了大量的特征点优化的计算，只保留了关键帧的轨迹，从而构建了所谓的位姿图

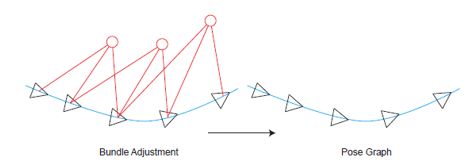
位姿图优化中的节点表示相机位姿，边表示两个节点之间相对运动的估计。
边可表示为

或按李群的写法：

然后构建误差eij：

所有的位姿顶点和位姿——位姿边构成了一个图优化，本质上是一个最小二乘问题，优化变量为各个顶点的位姿，边来自于位姿观测约束。记ε 为所有边的集合，那么总体目标函数为：

我们依然可以用Gauss-Newton、Levenberg-Marquardt 等方法求解此问题，除了用李代数表示优化位姿以外，别的都是相似的。

4. 回环检测

4.1. 概述

4.1.1. 回环检测的意义

前端提供特征点的提取和轨迹、地图的初值，而后端负责对这所有的数据进行优化。然而，如果像VO 那样仅考虑相邻时间上的关联，那么，之前产生的误差将不可避免地累计到下一个时刻，使得整个SLAM 会出现累积误差。长期估计的结果将不可靠，或者说，我们无法构建全局一致的轨迹和地图。

回环检测模块，能够给出除了相邻帧之外的，一些时隔更加久远的约束。回环检测的关键，就是如何有效地检测出相机经过同一个地方这件事。如果能够成功地检测这件事，就可以为后端的Pose Graph 提供更多的有效数据，使之得到更好的估计，特别是得到一个全局一致（Global Consistent）的估计。

4.1.2. 核心问题：

如何计算图像间的相似性

4.1.3. 准确率和召回率

准确率：算法提取的所有回环中，确实是真实回环的概率。
召回率：在所有真实回环中，被正确检测出来的概率。

为了评价算法的好坏，我们会测试它在各种配置下的P 和R 值，然后做出一条Precision-Recall 曲线。当用召回率为横轴，用准确率为纵轴时，我们会关心整条曲线偏向右上方的程度、100% 准确率下的召回率，或者50% 召回率时候的准确率，作为评价算法的指标。

值得一提的是，在SLAM 中，我们对准确率要求更高，而对召回率则相对宽容一些。由于假阳性的（检测结果是而实际不是的）回环将在后端的Pose Graph 中添加根本错误的边，有些时候会导致优化算法给出完全错误的结果。而相比之下，召回率低一些，则顶多有部分的回环没有被检测到，地图可能受一些累积误差的影响——然而仅需一两次回环就可以完全消除它们了。所以说在选择回环检测算法时，我们更倾向于把参数设置地更严格一些，或者在检测之后再加上回环验证的步骤。

4.2. 词袋模型

词袋，也就是Bag-of-Words（BoW），目的是用“图像上有哪几种特征”来描述一个图像。
字典中的单词，假设为w1、w2、w3。然后，对于任意图像A，根据它们含有的单词，可记为：

字典是固定的，所以只要用[1 1 0]T 这个向量就可以表达A 的意义。通过字典和单词，只需一个向量就可以描述整张图像了。

同理，用[2 0 1]T 可以描述图像B。如果只考虑“是否出现”而不考虑数量的话，也可以是[1 0 1]T ，这时候这个向量就是二值的。于是，根据这两个向量，设计一定的计算方式，就能确定图像间的相似性了。当然如果对两个向量求差仍然有一些不同的做法，比如说对于a，b∈ RW，可以计算：

其中范数取L1 范数，即各元素绝对值之和。请注意在两个向量完全一样时，我们将得到1；完全相反时（a 为0 的地方b 为1）得到0。这样就定义了两个描述向量的相似性，也就定义了图像之间的相似程度。

4.3. 字典创建

4.3.1. K均值算法

字典由很多单词组成，而每一个单词代表了一个概念。一个单词与一个单独的特征点不同，它不是从单个图像上提取出来的，而是某一类特征的组合。所以，字典生成问题类似于一个聚类问题。当我们有N 个特征点，想要归成k 个类，那么用K-means 来做，主要有以下几个步骤：

4.3.2. k叉树字典

使用一种k叉树来表达字典。它的思路很简单，类似于层次聚类，是K-means的直接扩展。假定我们有N 个特征点，希望构建一个深度为d，每次分叉为k 的树，那么做法如下：


实际上，最终我们仍在叶子层构建了单词，而树结构中的中间节点仅供快速查找时使用。这样一个k 分支，深度为d 的树，可以容纳kd个单词。另一方面，在查找某个给定特征对应的单词时，只需将它与每个中间结点的聚类中心比较（一共d 次），即可找到最后的单词，保证了对数级别的查找效率。

4.4. 相似度计算

考虑权重以后，对于某个图像A，它的特征点可对应到许多个单词，组成它的Bag-of-Words：

对于给定的VA和VB，通过某些方式即可比较其相似度。如L1范数：

5. 建图

所谓地图，即所有路标点的集合。一旦我们确定了路标点的位置，那就可以说我们完成了建图。SLAM 作为一种底层技术，往往是用来为上层应用提供信息的。应用层面对于“定位”的需求是相似的，他们希望SLAM 提供相机或搭载相机的主体的空间位姿信息。而对于地图，则存在着许多不同的需求。

稀疏地图只建模感兴趣的部分，也就是前面说了很久的特征点（路标点）。
稠密地图是指，建模所有看到过的部分。
在稠密重建，我们需要知道每一个像素点（或大部分像素点）的距离，那么大致上有以下几种解决方案：

1. 使用单目相机，利用移动相机之后进行三角化，测量像素的距离。
2. 使用双目相机，利用左右目的视差计算像素的距离（多目原理相同）。
3. 使用RGB-D 相机直接获得像素距离。
   前两种方式称为立体视觉（Stereo Vision），其中移动单目的又称为移动视角的立体视觉（Moving View Stereo）。相比于RGB-D 直接测量的深度，单目和双目对深度的获取往往是“费力不讨好”的——我们需要花费大量的计算，最后得到一些不怎么可靠的¬深度估计。当然，RGB-D 也有一些量程、应用范围和光照的限制，不过相比于单目和双目的结果，使用RGB-D 进行稠密重建往往是更常见的选择。而单目双目的好处，是在目前RGB-D还无法很好应用的室外、大场景场合中，仍能通过立体视觉估计深度信息。

5.1. 单目稠密建图

在稠密深度图估计中，我们无法把每个像素都当作特征点，计算描述子。因此，稠密深度估计问题中，匹配就成为很重要的一环：如何确定第一张图的某像素，出现在其他图里的位置呢？这需要用到极线搜索和块匹配技术。然后，当我们知道了某个像素在各个图中的位置，就能像特征点那样，利用三角测量确定它的深度。

左边的相机观测到了某个像素p1。由于这是一个单目相机，我们无从知道它的深度，所以假设这个深度可能在某个区域之内，不妨说是某最小值到无穷远之间：(dmin，+∞)。因此，该像素对应的空间点就分布在某条线段（本例中是射线）上。在另一个视角（右侧相机）看来，这条线段的投影也形成图像平面上的一条线，我们知道这称为极线。
在p1 周围取一个大小为w * w 的小块，然后在极线上也取很多同样大小的小块进行比较，就可以一定程度上提高区分性。这就是所谓的块匹配。
然后计算小块与小块间的差异，存在很多计算方法，如

它计算的是两个小块的相关性，接近0表示两个图像不相似，而接近1表示相似。

5.2. RGB-D稠密建图

除了使用单目和双目进行稠密重建之外，在适用范围内，RGB-D 相机是一种更好的选择。在RGB-D 相机中可以完全通过传感器中硬件测量得到深度，无需消耗大量的计算资源来估计它们。并且，RGB-D 的结构光或飞时原理，保证了深度数据对纹理的无关性。即使面对纯色的物体，只要它能够反射光，我们就能测量到它的深度。这亦是RGB-D 传感器的一大优势。

利用RGB-D 进行稠密建图是相对容易的。不过，根据地图形式不同，也存在着若干种不同的主流建图方式。最直观最简单的方法，就是根据估算的相机位姿，将RGB-D 数据转化为点云（Point Cloud），然后进行拼接，最后得到一个由离散的点组成的点云地图（Point Cloud Map）。在此基础上，如果我们对外观有进一步的要求，希望估计物体的表面，可以使用三角网格（Mesh），面片（Surfel）进行建图。另一方面，如果希望知道地图的障碍物信息并在地图上导航，亦可通过体素（Voxel）建立占据网格地图（Occupancy Map）。