Quantum Tensor Networks in a Nutshell

目录

1. quantum Legos
2. From Tensors to Networks
3. Bending and Crossing Wires
4. Diagrammatic SVD
5. Matrix Product States
6. Counting by Tensor Contrsction
　　Counting Boolean Formula Solutions
　　Counting Graph Colorings
7. Frontiers in Tensor Networks
　　Acknowledgments
　　Regerences

A.Tensors and Tensor Products

1、量子基础

• 张量是一个数学概念，它是多线性映射的概括总结和推广，即：多变量函数关于每一个变量都是线性的。
• 张量网络是由张量缩并结合起来的张量的可数集。
  张量网络以一种直观的图形语言展现出来。量子线路是一种特殊的张量网络，由特定类型的张量排列形成。
• 张量网络的著名的应用是：1D Matrix Product States（MPS）、Tensor Trains(TT)、Tree Tensor Networks(TTN)、the Multi-scale Entanglement Renormalization Ansatz(MERA)、Projected Entangled Pair States(PEPS)
• 利用简单、常规结构的张量网络去近似一个复杂量子态的方法，本质上应用了可以保留量子态最重要特性的有耗数据压缩。
• 下图表示了张量网络是如何以多种多样的方式表达或者近似一个量子态$|\psi ⟩$:

• 本文作者假设读者已经知晓：量子理论、线性代数、张量

2、从张量到网络

1、画张量
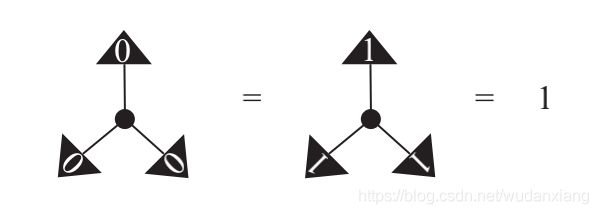
在张量图示中，一个张良是一个带有标签的图形，方形或者三角形，带有0条或者多条输出边，指向上；带有0条或者多条输入边，指向下。单独的边分别对应上下指标。表示边的线如果必要的话标记上表示的指标或者它们对应的向量空间，$(0,0)$阶的张量没有任何边，表示一个复数。例如，图(a)表示张量${\psi }^i$有一个上指标，是一个向量。图(b)表示张量$A_k^j$是一个矩阵，图©表示张量$T_{jk}^i$.
2、张量并列
当有两个或者更多不连接的张量出现在同一个图里，它们通过张量积相乘，在抽象索引表示法中，张量积符号省略，张量可以很自由的穿过彼此移动，有时称为平面变形。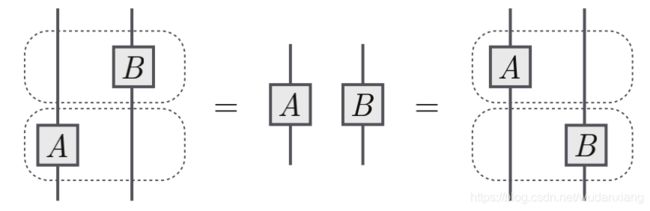
上图所对应的方程如下：$(I\otimes B)(A\otimes I)=(A\otimes B)=(A\otimes I)(I\otimes B)$.其中，也用线来表示恒等张量$I$.线允许穿过张量符号和其他线只要线的最后指向不变即可。下图没有对线标记，如果标记的话，可以记为：$Q_b^{deg}{R}_{ac}^f.$

3、连接线
利用一条边连接两个张量的边表示对应指标的缩并(求和)。

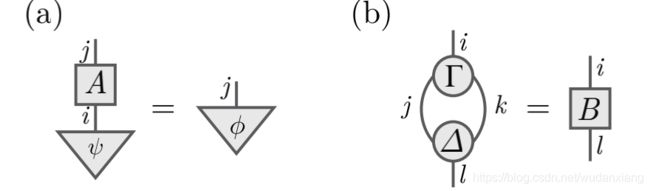
图(a)表示一个矩阵乘以一个向量得到一个向量，图(a)等价于下述表达：$$A_i^j{\psi }^i={\varphi }^j$$注意到，表示指标$i$的线完全连接起来了，因此对应的指标被缩并了。使用$Einsteinsummationconvention$,任意的指标在同一项里出现两次(上下指标各一次)就缩并。图(b)缩并两个3阶张量的指标，等价于：$${\Gamma }_{jk}^i{\Delta }_l^{jk}=B_l^i.$$

两个及其以上的张量在一个图里形成一个张量网络，如果在这个张量网络中任何一个张量都没有边我们称之为充分缩并：计算得到一个复数，是一个标量。

4、连接到量子计算符号
张量是多重线性映射，可以在任意给定的基下展开，按照它的组成部分表达出来，在量子信息科学里，每一个$Hilbertspace$有一组计算基${\left\{|k⟩\right\}}_k$并且张量可以在这组基下展开。$$T=\sum _{ijk}{T}_{jk}^i|i⟩⟨jk|.$$其中$T_{jk}^i$是在计算基下张量的组合部分。

例1（$ϵ$张量）
一个张量是完全反对称的，如果交换任意指标对它的符号就改变：$A_{ij}=-A_{ji}$,$ϵ$张量用来表达这种完全反对称$Levi-Civita$记号，在2维的情形表达如下：$${ϵ}_{00}={ϵ}_{11}=0,{ϵ}_{01}=-{ϵ}_{10}=1$$$ϵ$张量可以用来计算矩阵的行列式，在2维的情形，有：$det(S)={ϵ}_{ij}{S}_0^i{S}_1^j.$利用上式，可以得到：
　　　
对应的方程是：$${ϵ}_{ij}{S}_m^i{S}_n^j=det(S){ϵ}_{mn}.$$按照量子力学，$ϵ$对应一个$2-qubit$纯态：$$\frac{1}{\sqrt{2}}|ϵ⟩=\frac{1}{\sqrt{2}}(|01⟩-|10⟩).$$这个量子态在任意一个形为$U\otimes U$的变换下是不变的，(其中$U$是$2\times 2$酉矩阵),仅仅相差一个全局相位因子。

例2（并发和纠缠）
给定一个$2-qubit$纯量子态$|\psi ⟩$,它的并发($concurrence$) $C(\psi )=|C\prime (\psi )|$是下列张量网络表达的绝对值：

其中$\bar{\psi }$是$\psi$在计算基下的复共轭。并发是一种纠缠单配性，是一种从态到非负正实数的函数，测量态是如何纠缠的。$|\psi ⟩$是纠缠的当且仅当并发是大于等于0的数。现在考虑将任意一个酉操作作用在$|\psi ⟩$上，即：$$C((U_1\otimes U_2)|\psi ⟩)=C(\psi )|det(U_1)det(U_2)|.$$因为$|det(U_1)|=|det(U_2)|=1$,这就得到，并发在局部酉变换下是不变量。因为局部酉变换并不能改变量子态的纠缠数量。更复杂的不变量可以被如下张量网络表示：

如果$|\psi ⟩$是一个$3-qubit$的量子态，$\tau (\psi )=2|{\tau }^{\prime }(\psi )|$表示纠缠不变性。
不使用$ϵ$张量，也可以构造不变性，例如$Kempeinvariant$是$3-qubit$纠缠不变性：$$K(\psi )={\psi }^{ijk}{\bar{\psi }}_{ilm}{\psi }^{nlo}{\bar{\psi }}_{pjo}{\psi }^{pqm}{\bar{\psi }}_{nqk}.$$
画出等价的张量网络。

例3（量子线路）
量子线路是一种特殊的张量网络子类，它被广泛的应用在量子信息领域。在量子线路图中每一条水平线表示一个与量子子系统（典型的单比特）关联的希尔伯特空间，张量附着在线路上，表示作用在这些子系统上的酉矩阵，被称作量子门，另外的记号用来表示测量。考虑一个简单的量子线路，它可以生成贝尔态。由两个张量组成，一个$Hadamardgate(H)$和一个$controlledNOTgate(CNOT)$:

CNOT和Hadamard 门被定义为：$$CNOT=\sum _{ab}|a,a\oplus b⟩⟨a,b|$$$$H=\frac{1}{\sqrt{2}}\sum _{ab}(-1{)}^{ab}|a⟩⟨b|$$
例4（COPY和XOR张量）
CNOT门可以看作2个3阶张量的缩并：

上边的张量称作COPY张量，当所有的指标值相等时，它等于1，否则等于0.

因此，COPY门作用可以复制二进制输入0和1：

下边的张量称作奇偶张量或者XOR张量，当它的指标包含偶数个1时它等于1，否则等于0.
XOR张量和COPY张量通过Hadamard门想联系：

因此在另外一组基下，XOR张量可以看作复制操作：$$\frac{1}{\sqrt{2}}XOR|+⟩=|+⟩|+⟩,$$$$\frac{1}{\sqrt{2}}XOR|-⟩=|-⟩|-⟩$$其中$|+⟩:=H|0⟩$和$|-⟩:=H|1⟩$按照组成部分来说：$$COP{Y}_k^{ij}=(1-i)(1-j)(1-k)+ijk,$$$$XO{R}_s^{qr}=1-(q+r+s)+2(qr+qs+sr)-4qrs$$
因此CNOT门做张量缩并后得到：$$\sum _{m}COP{Y}_i^{qm}XO{R}_{mj}^r=CNO{T}_{ij}^{qr}.$$

3、弯曲交叉线

1、帽型和杯型
线是用来表示张量指标对的缩并，某种线结构可作为独立的张量，以下介绍3中线张量：
恒等张量(a)是用来做指标缩并，通过连接对应的边。杯型张量(b)和帽型张量©是通过弯曲对应的张量的边来上移和下移张量指标。在计算基下展开：$$I=\sum _{ij}{\delta }_j^i|i⟩⟨j|=\sum _k|k⟩⟨k|$$$$|\cup ⟩=\sum _{ij}{\delta }^{ij}|ij⟩=\sum _k|kk⟩$$$$⟨\cap |=\sum _{ij}{\delta }_{ij}⟨ij|=\sum _k⟨kk|$$

2、蛇形方程
如果向上弯曲然后向下弯曲一个指标等同于什么操作都没有做，这就是蛇形方程或者之字形方程。
　　

在抽象索引表示法中，蛇形方程简洁地表示为：${\delta }^{ij}{\delta }_{jk}={\delta }_k^i={\delta }_{kj}{\delta }^{ji}$

3、SWAP门
交叉两条线是交换两个向量空间的顺序，对应着量子计算中的SWAP门。如果两条线路表示地是同一个向量空间，可以理解为交换两个子系统地状态，如图a。
方程b说明SWAP操作是自逆的。表示为:$swa{p}_{kl}^{ij}={\delta }_k^j{\delta }_l^i$,或者在一组计算基下展开为：SWAP=${\sum }_{ij}|ij⟩⟨ji|$.

用3个CNOT门可以实现SWAP操作：

SWAP是一种简单的非平凡的置换张量，更复杂的置换张量可以由${\delta }_j^i$张量构建。

4、转置
给定$A_j^i$,可以使用杯型和帽型来改变指标的位置。这相当于在计算基上相应的线性映射的转置。

5、迹
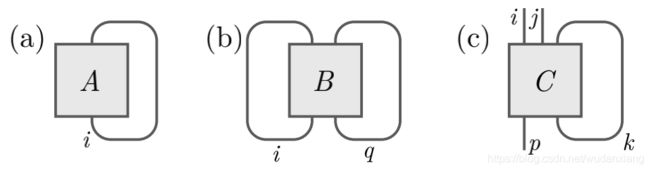
在张量网络标记中，迹是通过合理地连接一个张量中输出线和对应的输入线来完成的。图a表示迹$A_i^i$,图b表示迹$B_{iq}^{iq}$.偏迹是仅仅缩并一些输出和对应的输入，图c表示张量$C_{pk}^{ijk}$。

例5（偏迹）
左边的图表示$|\psi ⟩⟨\psi |$对第二系统的偏迹。
可以把弯曲的线解释为杯型和帽型，把交叉线解释为SWAP。
　　
例6（贝尔态的偏迹）
如果选择$|\psi ⟩=|\cup ⟩$,即：$|\psi ⟩$是一个非归一化的贝尔态，得到：

例7（$ϵ$和SWAP之间的关系)
对于2阶张量，定义它的反对称化为：$T^{[ij]}=\frac{1}{2}(T^{ij}-T^{ji})$只有指标的维数相同的指标才可以定义反对称化。完全反对称$ϵ$张量与SWAP门之间的关系如下：

或者表达为：$${ϵ}^{kl}{ϵ}_{ij}={\delta }_i^k{\delta }_j^l-{\delta }_j^k{\delta }_i^l$$对任意的张量，$T^{ij}$(每个指标都是2维的)，则$T^{[ij]}=\frac{1}{2}{ϵ}^{kl}{ϵ}_{ij}{T}^{ij}.$
例8（杯型和 $ϵ$ 态的量子线路）
例9（map-态的对偶性）
6、$†$ 和复共轭
$(p,q)$阶张量$T$的自伴是$T^{†}$,是一个$(q,p)$阶张量。定义如下：$⟨x,Ty⟩=⟨T^{†}x,y⟩$,对任意的$x,y$。图示自伴的张量网络是将原本的张量网络的输入和输出线换位置，则张量的序就相反了。$dagger$操作把希尔比特空间的向量一对一地映射到对偶向量空间中，反之亦然，利用$Rieszrepresentationtheorem$。即：$|a{⟩}^{†}=⟨a|$。$dagger$是反线性的(或共轭线性)运算，$(cT+dU{)}^{†}=\bar{c}{T}^{†}+\bar{d}{U}^{†}$，这也意味着它不能被线性杯型和帽型单独表示，不像转置。但是可以在同一组基下由转置和复共轭表示。如下图所示：
对向量和对偶向量，弯曲向量的一条线，产生对偶向量的复共轭，反之亦然。

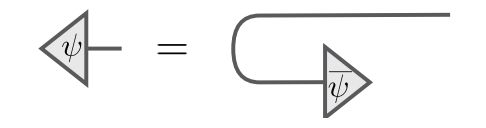
7、指标位置
使用杯型和帽型向前和向后弯曲张量线；使用SWAP交换张量线的顺序；
给定一个张量$T_j^i$,使用杯型和帽型可以重排指标的高低和位置，得到：$$T_j^i,T^{ij},T_{ij},T_i^j,T_i^j,T^{ji},T_{ji},T_j^i$$共8中可能的形状。如果指标数超过2个还可以加上SWAP操作重拍顺序，对n个指标的张量，共有$n!\cdot 2^n$种不同的方式，但是有多余的计算，在上例中，$T_j^i=T_j^i,T_i^j=T_i^j$,如图所示：

因此，张量$T_j^i$只有6种不同的形状：

4、图解奇异值分解

例10（纠缠拓扑）
例11（并发-part II）
例12（纯化）

5、矩阵乘积态

例13（MPS的近似错误）
例14（对GHZ态的MPS分解）
例15（W态的MPS分解）
例16（AKLT模型）
定义17（$R\acute{e}nyi$和von Neumann 熵）

6、用张量缩并来计数

1、计数布尔公式解
定义18（布尔张量类）
定理19（计数SAT解）
例子20（从Tofolli到AND）
例子21（从AND到Hadamard）
例子22（De Morgan定律）
2、计数图像着色
定理23（平面图3-着色）
例子24（量子计算中的${ϵ}_{abc}$的物理实现）

7、张量网络的前沿

附录A：张量和张量积

• 张量积$\otimes$的定义：$V$、$W$是数域$K$上的两个有限维向量空间，则$V\otimes W$也是$K$上的一个向量空间，如果${\left\{e_j\right\}}_j$和 ${\left\{f_k\right\}}_k$分别是$V$、$W$的基，则${\left\{e_j\otimes f_k\right\}}_{jk}$是$V\otimes W$的基。因此$dim(V\otimes W)=dimVdimW$。两个独立的向量$v\in V$和$w\in W$的张量积为：$v\otimes w$。张量积是一个双线性映射：$V\times W\to V\otimes W$，即对输入的变量都是线性的。对有限维空间可以得到两个向量的张量积的标准基下的坐标通过各自向量的标准基下的坐标的克罗内克积得到：$(v\otimes w{)}^{jk}=v^j{w}^k$.由于双线性映射$\otimes$把很多不同的向量对$(v,w)$映为同一个积向量：$v\otimes (sw)=(sv)\otimes w=s(v\otimes w)$,其中$s\in K$。张量积空间中的内积：${⟨v_1\otimes w_1,v_2\otimes w_2⟩}_{V\otimes W}={⟨v_1,v_2⟩}_V{⟨w_1,w_2⟩}_W$。
• 张量$T$的定义：张量$T$是同一个数域$K$上，有限个线性空间的张量积中的元素。$V^{\ast }$是$V$的对偶空间，是$V\to K$的线性映射组成的空间，也是一个线性空间。
• $(p,q)$阶张量的定义：$$T\in W_1\otimes W_2\otimes \cdots \otimes W_p\otimes V_1^{\ast }\otimes V_2^{\ast }\otimes \cdots \otimes V_q^{\ast }$$
  ${\left\{{e^{(i)}}_k\right\}}_k$是每一个向量空间$W_i$的基，${\left\{{\eta }^{(i)k}\right\}}_k$是每一个对偶空间$V_i^{\ast }$的基。$T$展开成这些基向量的张量积：
  $$T=T_{j_1\dots j_q}^{i_1\dots i_p}{e}_{i_1}^{(1)}\otimes \cdots \otimes e_{i_p}^{(p)}\otimes {\eta }^{(1)j_1}\otimes \cdots \otimes {\eta }^{(q)j_q}$$其中$T_{j_1\dots j_q}^{i_1\dots i_p}$是$T$在基下展开的系数。此处采用$Einsteisummationconvention$,一般基向量有下指标（协变指标），对偶基向量有上指标（抗变指标）。
• 简单张量：如果一个张量可以写成基础向量空间中元素的张量积：$T=v^{(1)}\otimes \cdots \otimes v^{(q)}\otimes {\phi }^{(1)}\otimes \cdots \otimes {\phi }^{(p)}$,则称这个张量是简单张量，这也是可分张量的一个特性。即可分张量是简单张量。任何一个张量是简单张量的线性组合。
• 缩并：对任意一个向量空间$W$，存在唯一的双线性映射$W\otimes W^{\ast }\to K,w\otimes \varphi \mapsto \varphi (w)$,我们把它称为一个自然配对，其中对偶向量把主向量映射为一个数。可以在一个张量中应用这种银蛇到任意的对上来匹配主空间和对偶空间。我们把它称为对应的上下指标的缩并。例如，如果$W_1=V_1$,在$T$上可以缩并对应的指标：$$\begin{array}{l}{C}_{1,1}(T)\\ =T_{j_1\dots j_q}^{i_1\dots i_p}{\eta }^{(1)j_1}(e_{i_1}^{(1)})\otimes \cdots \otimes e_{i_p}^{(p)}\otimes {\eta }^{(2)j_2}\otimes \cdots \otimes {\eta }^{(q)j_q}\\ =T_{k{j}_2\dots j_q}^{k{i}_2\dots i_p}{e}_{i_2}^{(2)}\otimes \cdots \otimes e_{i_p}^{(p)}\otimes {\eta }^{(2)j_2}\otimes \cdots \otimes {\eta }^{(q)j_q}\end{array}$$

        因为对偶基的特性是：${\eta }^{(1)j_1}(e_{i_1}^{(1)})={\delta }_{i_1}^{j_1}$,因此缩并使得指标的影响消除，使得张量的阶数减少$(1,1)$阶。

• $(1,0)$阶张量是一个向量，$(0,1)$阶的张量是一个对偶向量，$(0,0)$阶的张量是一个数。$(p,q)$阶张量是向量到向量的多线性映射：$$T^{\prime }：V_1\otimes \cdots \otimes V_q\to W_1\otimes \cdots \otimes W_p$$$$T^{\prime }(v^{(1)}\otimes \cdots \otimes v^{(q)})=T_{j_1\dots j_q}^{i_1\dots i_p}{e}_{i_1}^{(1)}\otimes \cdots \otimes e_{i_p}^{(p)}\times {\eta }^{(1)j_1}(v^{(1)})\times \cdots \times {\eta }^{(q)j_q}(v^{(q)})$$将张量乘积$T$和向量一起映射，则缩并对应的指标，但是这不是唯一的解释，我们也可以看做映射对偶向量为对偶向量：$$T^{\prime \prime }：W_1^{\ast }\otimes \cdots \otimes W_q^{\ast }\to V_1^{\ast }\otimes \cdots \otimes V_p^{\ast }，$$$$T^{\prime \prime }({\phi }^{(1)}\otimes \cdots \otimes {\phi }^{(q)})=T_{j_1\dots j_q}^{i_1\dots i_p}{\phi }^{(1)}(e_{i_1}^{(1)})\times \cdots \times {\phi }^{(p)}(e_{i_p}^{(p)})\times {\eta }^{(1)j_1}\otimes \cdots \otimes {\eta }^{(q)j_q}.$$本质上，我们可以利用对偶把任意的向量空间移动到箭头的另一边：$$W\otimes V^{\ast }\cong K\to W\otimes V^{\ast }\cong V\to W\cong V\otimes W^{\ast }\to K\cong W^{\ast }\to V^{\ast },$$其中所有的箭头表示线性映射，所有输入的向量被对应的对偶基向量映射为数，因为输入的对偶向量映射对应的向量为一个数。
• 如果在展开张量$T$的时候在同一组基下将输入向量$v^{(k)}$也展开，就会得到带有下列展开系数的方程：$$T^{\prime }(v^{(1)}\otimes \cdots \otimes v^{(q)}{)}^{i_1\dots i_p}=T_{j_1\dots j_q}^{i_1\dots i_p}{v}^{(1)j_1}\dots v^{(q)j_q}.$$
  这使得我们开始使用张量的$abstractindexnotation$,在这种表示法中指标不再表示在一组特殊的基下张量的组成，而是张量的阶。张量基由张量符号写在一起来代替，在每一项里，任何重复的指标符号必须出现在上标和下标位置，并且表示对这些指标的缩并。因此，$x^a$表示一个向量（有一个协变指标），${\omega }_a$是一个对偶向量（有一个抗变指标），$T_c^{ab}$是一个$(2,1)$阶张量，有两个协变指标和一个抗变指标。$S_{cde}^{ab}{x}^c{y}^d{P}_a^e$表示一个$(2,3)$阶张量$S$，一个$(1,1)$阶张量$P$,和两个向量$x$和$y$的缩并，结果得到一个$(1,0)$阶有一个不缩并的指标$b$的张量。
• 在很多应用中，例如在微分几何中，与一个张量相关联的向量空间经常是$V$与自身或者与其对偶空间$V^{\ast }$的张量积，这就意味着任意上下指标对是可以缩并的，==并且导致张量的组成部分在基变换下以一种特殊的方式变换。==这种特殊类型的张量称为向量空间$V$上的$(p,q)$阶张量。本文中我们采用更一般的定义，我们假设${\left\{V_k\right\}}_k$和${\left\{W_k\right\}}_k$是两个不同的向量空间。