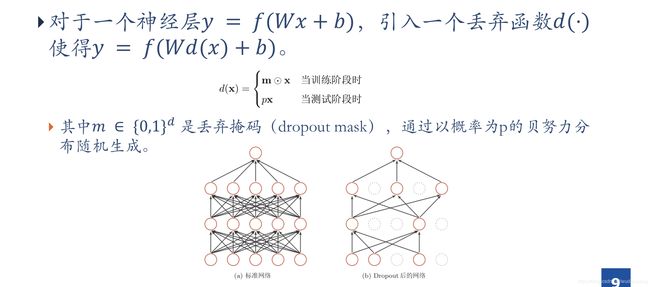
深度学习中的正则化
测试误差来源分析
权重衰减L1 正则化和L2正则化
数据增强与提前终止
Dropout
稀疏表示
测试误差来源分析主要结论：
测试误差一般来源于偏差（Bias）和方差（Variance）
当偏差大的时候出现欠拟合，当方差大的时候出现过拟合。
解决方法：
当偏差大的时候，增加特征个数（使用更复杂的模型）来优化；
当方差大的时候，增加样本个数或者正则化来优化。
偏差和方差的定义
估计变量 x x x的均值：
假设 x x x的平均值是 μ \mu μ,方差是 σ 2 \sigma^2 σ2,现已知 x x x的一些样本点（但不全知道）的情况下如何求 μ \mu μ呢？例如已知 N N N个样本点 x 1 , x 2 , . . . , x N {x^1,x^2,...,x^N} x1,x2,...,xN。
求 μ \mu μ的方法：
m = 1 N ∑ i = 1 N x i ≠ μ m = \frac{1}{N}\sum_{i=1}^Nx^i\neq\mu m=N1∑i=1Nxi=μ
E [ m ] = E [ 1 N ∑ i = 1 N x i ] = 1 N ∑ i = 1 N E [ x i ] = μ E[m] = E[\frac{1}{N}\sum_{i=1}^Nx^i] = \frac{1}{N}\sum_{i=1}^NE[x^i] = \mu E[m]=E[N1∑i=1Nxi]=N1∑i=1NE[xi]=μ
m m m的方差为（ m m m的方差取决于样本的个数）：
V a r [ m ] = σ 2 N Var[m] = \frac{\sigma^2}{N} Var[m]=Nσ2
s 2 = 1 N ∑ i = 1 N ( x n − m ) 2 s^2 = \frac{1}{N}\sum_{i=1}^N(x^n - m)^2 s2=N1∑i=1N(xn−m)2
E [ s 2 ] = N − 1 N σ 2 ≠ σ 2 E[s^2] = \frac{N-1}{N}\sigma^2 \neq \sigma^2 E[s2]=NN−1σ2=σ2
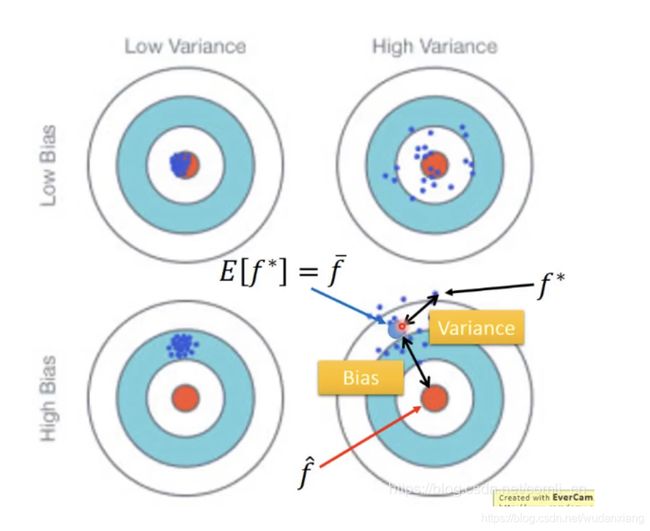
右下角：实际目标为红色点，而算出的是蓝色的小点，取这些蓝色小点的期望为 f ^ = E ( f ∗ ) \hat{f}=E(f^*) f^=E(f∗)用如图所示的蓝色大点表示，那么蓝色大点与红色点之间的距离就是偏差，而蓝色大点与蓝色小点之间的距离就是方差。
左上角：偏差和方差都比较小；
右上角：偏差较小方差较大；
左下角：偏差较大方差较小。
偏差和方差由什么因素决定？
- 方差
方差由模型的复杂度决定，模型越复杂方差越大。
下图中每条函数曲线都是从同一分布中随机抓取相同数量的样本分别学习得到的预测曲线。
当采用比较简单的模型时得到的预测曲线比较一致；
当使用比较复杂的模型时得到的预测曲线杂乱无章；
就想比较聚集的蓝色小点和比较分散的蓝色小点。 - 偏差
如果把所有的 f ∗ f^* f∗做平均它是否会接近 f ^ \hat{f} f^呢？
先假设一个 f ^ \hat{f} f^,如下图：
分别用一次式、三次式和五次式为模型对5000个不同的样本组进行学习并绘制出预测曲线，并用黑色曲线表示假设的 f ^ \hat{f} f^，用蓝色去彪表示对5000条预测曲线求平均后的曲线，如下图：
模型越复杂预测曲线的平均值曲线与真实曲线越相近。
这是因为：用简单的模型学习预测函数时它的值域会比较小，分布范围也小；用复杂模型学习预测函数时它的值域比较大，分布范围也大。
如下图：
受偏差和方差影响的测量误差
红线：由偏差引起的误差；
绿色：由方差引起的误差；
蓝色：测量误差
分两种情况来进行优化
- 偏差比较大的情况：
当偏差大的时候通过增加特征个数（使用更复杂的模型）来优化。 - 方差比较大的情况：
当方差大的时候通过增加样本个数或者正则化来优化。————权重衰减
- 增加数据：
正则化：
神经网络两个特点：
1、过度参化；
2、拟合能力强；
会导致————泛化性差！
正则化的定义：一类通过限制模型复杂度，从而避免过拟合，提高泛化能力的方法，包括引入一些约束规则，增加先验、提前停止等。
深层神经网络的优化和正则化是既对立又统一的关系：
一方面希望优化算法能找到一个全局最优解（或者较好的局部最优解）；
另一方面不希望模型优化到最优解，这可能陷入到过拟合；
优化和正则化的统一目标是期望风险最小化！
提高神经网络泛化能力的方法：
- L1和L2正则化
- 提前停止
- SGD（随机梯度下降）
- Dropout
- 数据增强
- 权重衰减
所有的P-范数都是惩罚更大的权重
p < 2 p<2 p<2时，趋向于创造稀疏（即：很多0权重）
p > 2 p>2 p>2时，趋向于得到更小的权重
权重衰减正则化与L2正则化等价问题
- 第一维代表水平方向，在水平方向上 w ∗ w^* w∗移动时，目标函数增加的不多，因为目标函数 J J J的Hessian矩阵在第一维的特征值小，即目标函数对这个方向没有强烈的偏好，所以正则化对该方向有强烈的影响。
- 第二维表示竖直方向，在竖直方向上 w ∗ w^* w∗移动时，目标函数增加的很多，因为目标函数 J J J的Hessian矩阵在第二维的特征值大，即目标函数对这个方向有很强烈的偏好，所以正则化对该方向无强力的影响。
数据增强
图像数据的增强主要是通过算法对图像进行转变，引入噪声等方法来增强数据的多样性。
图像数据增强的方法：
- 旋转
- 翻转
- 缩放
- 平移
- 加噪声
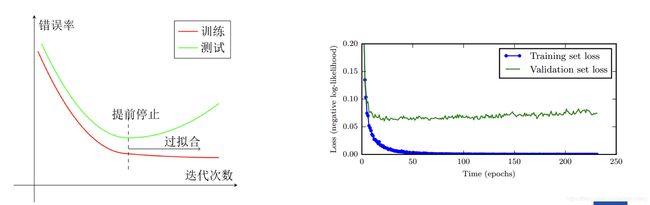
提前终止
使用一个验证集（Validation Dataset）来测试每一次迭代的参数在验证集上是否最优。如果在验证集上的错误率不再下降，就停止迭代。
Dropout
1、首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变（上图中虚线为部分临时删除的神经元）
2、然后把输入 x x x通过修改后的网络向前传播，再把得到的损失结果通过修改的网络反向传播，一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（ w , b w,b w,b）
3、继续重复1、2这一过程：
- 恢复被删除的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
- 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除的神经元的参数）
- 对一小批训练样本，先向前传播然后反向传播损失并根据随机梯度下降法封更新（ W , b W,b W,b）（没有被删除的那一部分参数得到更新，删除的神经元参数保持被删除前的结果）