matlab 机器人工具箱3-机械臂及运动学
本文主要参考清华大学出版社的《机器人仿真与编程技术》一书
机械臂D-H建模的相关知识的主要参考
《机器人学导论》 John J.Craig 著
《Mdern Robotics Mechanics ,Planning and Control》Kevin M 等人著
https://blog.csdn.net/lingchen2348/article/details/78561906前辈写的csdn的文章
https://wenku.baidu.com/view/03d586024afe04a1b171de8d.html一个机器人学的ppt
《A kinematic notation for lower-pair mechanisms based on matrices》修正D-H建模
主要使用的就是D-H四参数:
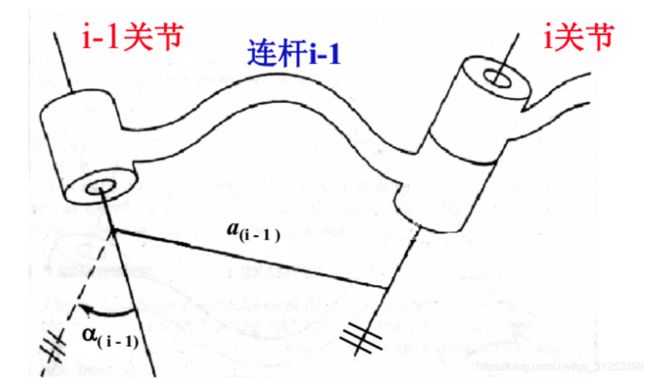
(1)连杆i-1的长度。是指图中a(i-1)所示的距离。表示i-1关节的轴线与i关节的轴线的垂直距离。
(2)连杆i-1的扭角。是指图中α(i-1)所示的角度。空间两条直线即使不相交也存在夹角,那么,扭角α(i-1)就是关节i-1与关节i轴线的夹角。
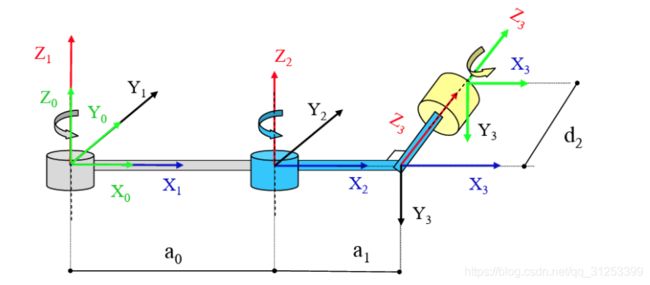
(3) 连杆i 相对于连杆i-1的偏置di。下图中的di就是偏置。我们来看i关节的轴线,它与前后两个关节轴线各有一条公垂线(红线,下一个关节虽没画出来),这两条公垂线的距离就是连杆i相对连杆i-1的偏置。(请看清楚连杆i-1和连杆i的位置,蓝字)。
(4) 关节角θi。连杆i相对于连杆i-1绕i轴的旋转角度,图中右下角的θi,其实就是上图两条红色公垂线的夹角。
下面3个加粗标题就是DH建模的主要规则:
先建立中间坐标系{i},后两端坐标系{0}、{n}
坐标系{0}和{n}的规定
Z0轴沿关节轴1的方向,关节变
量1为零时, 坐标系{0}与{1}重合
关节1是旋转关节时, d0=0,
关节1是移动关节时, θ0=0
Zn轴沿关节轴n-1的方向,关节变
量n-1为零时, 坐标系{n-1}与{n}重合
关节n-1是旋转关节时, dn=0,
关节n-1是移动关节时, θn=0
建系的原则
1)确定Z轴:找出关节轴线及关节转向采用右手定则确定Z;
2)确定原点:如果两相邻轴线Zi与Zi+1不相交,则公垂线与轴线i的交
点为原点,注意平行时原点的选择应使偏置为零;如果相交则交点
为原点,注意:如果重合则原点应使偏置为零;
3)确定X轴:两轴线不相交时,X与公垂线重合,指向从i到i+1;
若两轴线相交,则X是两轴线所成平面的法线X= - +Zi × Zi+1 ;
注意:如果两轴线重合,则X轴与轴线垂直且使其他连杆参数为零;
4)按右手定则确定Y ;
5)当第一个关节变量为零时,规定{0}与{1}重合,对于
末端坐标系{n},原点与X任选,希望坐标系{n}使杆参数尽量为零。
以上区域选自:https://blog.csdn.net/lingchen2348/article/details/78561906前辈写的csdn的文章
我自己的思路就是先通过给定的模型,给每个关节创建相对应的坐标系,主要是确定xz轴以及坐标原点,之后测量xz的变换(角度和位移)就可以,具体的步骤如下:
-
首先确定每个关节的z轴,也就是关节的轴线方向,z的方向指向电机旋转的正向,也就是使用右手定则,大拇指指向z轴的正向,四指方向指向电机旋转的正向(做控制时,给电机一个正参数,电机旋转的方向)
-
之后确定坐标系原点,当前后两个轴线不相交,这个时候比较好理解,坐标系的原点就在对应的关节上,在轴i与轴i+1的公垂线与轴线的交点上。但是当两个轴线相交的时候,原点取在轴i与轴i+1的交点上,经常会出现坐标系i与i+1原点重合都在i+1的关节上,看上去i关节上没有坐标系。
-
确定x轴,两轴线不相交时,X与公垂线重合,指向从i到i+1;若两轴线相交,则X是两轴线所成平面的法线X= +-Zi+1 × Zi,也就是右手定律由i+1轴指向i轴,拇指代表的方向。(这里也写道的+-的情况,其实x轴正负都可以,一般情况为了计算方便,x轴方向尽量和前一个坐标系x轴方向一致)
-
之后就是确定参数,4个参数其实就是代表了x,z轴的平移和旋转。
-
在之后的参数中第i个关节的关于z中轴的参数都是i-1,关于x轴的参数都是i,比如:
现在D-H参数就确定下来了
下面是matlab部分:
机器人工具箱可以使用Link()创建一个连杆,具体的参数如下
L =Revolute(std): theta=q, d=2, a=3, alpha=0.785398, offset=0-
关节类型:默认旋转(0),1的话改为平移
-
theta关节角
-
d连杆偏移
-
a连杆长度
-
alpha连杆转角
-
offset关节偏移
之后建一个多连杆
L(1)=Link([0,0,1,0])
L(2)=Link([0,0,.8,0])
L(3)=Link([0,0,.6,0])
L
tree_link=SerialLink(L,'name','tree_link')显示如下
L =
Revolute(std): theta=q1 d=0 a=1 alpha=0 offset=0
Revolute(std): theta=q2 d=0 a=0.8 alpha=0 offset=0
Revolute(std): theta=q3 d=0 a=0.6 alpha=0 offset=0
tree_link =
tree_link:: 3 axis, RRR, stdDH, slowRNE
+---+-----------+-----------+-----------+-----------+-----------+
| j | theta | d | a | alpha | offset |
+---+-----------+-----------+-----------+-----------+-----------+
| 1| q1| 0| 1| 0| 0|
| 2| q2| 0| 0.8| 0| 0|
| 3| q3| 0| 0.6| 0| 0|
+---+-----------+-----------+-----------+-----------+-----------+这里为什么给饿了theta=0,显示是q1?因为D-H建模后,其他的参数都确定了,只有theta角会随着关节的旋转而变化,是一个随着后期运动而不断变换的值,0代表他的初始状态。q1代表变化量。比如
L=Link([0,0,1,0])
L.A(0)
L.A(pi)
ans =
1 0 0 1
0 1 0 0
0 0 1 0
0 0 0 1
ans =
-1 0 0 -1
0 -1 0 0
0 0 1 0
0 0 0 1可以看到绕z轴旋转了pi
当我们使用改进型D-H建模时就加上参数'modified'
L1=Link([0,2,3,pi/4,0])
L2=Link([0,2,3,pi/4,0],'modified')
L1.A(0)
L2.A(0)对比一下结果:
ans =
1 0 0 3
0 0.7071 -0.7071 0
0 0.7071 0.7071 2
0 0 0 1
ans =
1 0 0 3
0 0.7071 -0.7071 -1.414
0 0.7071 0.7071 1.414
0 0 0 1两者的区别参考:https://www.zhihu.com/question/22365926/answer/155391570
引用原文的说法就是标准的D-H建模(standard DH)建立坐标系的时候,将坐标系固定在该连杆的输出端(下一个关节),所以就使得i坐标系与i+1连杆对齐,而改进D-H建模(modified DH)方法就是i坐标系与i连杆对齐。标准的D-H在处理树形结构的时候会产生歧义,改进的DH不存在这个问题,虽然链状的串联机械臂不会表现出来,因为本人所学为改进式,所以默认的就是modified的。
当我们使用多个机械臂进行连续变换,求运动学正解的时候,使用机器人工具箱fkine(),其中的参数为每个关节的theta角的大小
L(1)=Link([0,0,1,0])
L(2)=Link([0,0,.8,0])
L(3)=Link([0,0,.6,0])
tree_link=SerialLink(L,'name','tree_link')
T = tree_link.fkine([0 0 0])
subplot(2,2,1)
title("T")
tree_link.plot([0 0 0])
subplot(2,2,2)
title("T1")
tree_link.plot([pi/2 0 0])
subplot(2,2,3)
title("T2")
tree_link.plot([pi/2 pi/2 0])
subplot(2,2,4)
title("T3")
tree_link.plot([pi/2 pi/2 pi/2])我们发现四个图都是从上个位置一直变换到最后的状态,图一1-2-3-4,图二2-3-4,图三3-4 ,图四4.测试一下就是tree_link.plot相当于改变了L的状态,后面的改变会影响前面的状态,是前面的图也进行了变换。如果我们 tree_link_new=SerialLink(L,'name','tree_link')对这个plot,效果也是一样,图i+1的状态会影响i的状态。我们想分开测试,需要定义新的L_new=Link...