[深度学习论文笔记][ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION
[ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION
Hongyi Zhang, Moustapha Cisse, Yann N. Dauphin and David Lopez-Paz
from MIT & FAIR
paper link
Overview
这篇文章提出了一种新的数据扩展方法。该方法简单有效。同时作者在文章中进行了详细的理论分析和实验分析,很有阅读价值。
Motivation
从ERM到VRM
当前网络优化方法大多遵循经验风险最小化方法(Empirical Risk Minimization, ERM),即使用采样的样本来估计训练集整体误差。一个对ERM的简明解释可以参考这里。[1]的研究证明模型体量固定,数据量足够,即可保证使用ERM时训练的收敛性。如今网络体量都很大,这就造成:
- 网络倾向于记忆训练样板,而不是泛化[2];
- 难以抵御分布外样本,如肉眼感官没有区别的对抗样本[3]。
解决这一问题的一个途径就是使用邻域风险最小化原则(Vicinal Risk Minimization, VRM),即通过先验知识构造训练样本在训练集分布上的邻域值。通常做法就是传统的数据拓展,如翻转,旋转,放缩等。但是这种做法过于依赖特定数据库,此外需要人类的先验知识 。
Method
本文的贡献是提出一种新的数据扩展方式,即使用线性插值的方法得到新的扩展数据。假设 (xi,yi),(xj,yj) ( x i , y i ) , ( x j , y j ) 是两个“训练数据-标签”对, λ λ 是0到1之间的值,得到的新拓展数据为:
当 λ λ 只取0,1的时候,本文提出的拓展方法则退化到了ERM的情景。
当然,有人可能会质疑线性插值是否过于简单。这里作者从奥卡姆剃刀的角度来解释,既然有效果,那模型肯定是越简单越好。
Experiments
作者的实验非常详尽。一方面覆盖面广,包含了在图像、语音、表格数据上的任务,同时也做了泛化能力、对手样本抵御能力的实验对照前文提出的ERM的两个缺点,而且还验证了该方法能够稳定GAN训练,吸引很多人的注意。这里只选取部分结果:
Image Classification Task
作为一种数据拓展方法,其有效性直接体现在测试模型所提升的精确度上,这里给出在Cifar-10/100上的结果:
Memorization of Corrupted Labels
遵从[2]中的实验设置,作者验证了使用了本文提出方法训练的模型能够破除网络对噪声标签的过拟合现象:
Robustness to Adversarial Examples
对FGSM白盒攻击,本文提出方法训练的模型top 1错误率是ERM模型top 1错误率好2.7倍,FGSM黑盒测试上好1.25倍,I-FGSM黑盒测试好40%。
Stabilization on GAN
训练GAN时,在判别器的训练过程中,都将真实样本和生成样本线性叠加得到扩展数据。
作者给出了一个演示范例,训练生成红色点来模拟蓝色点:
读后心得
总的来说,个人感觉这篇文章的完成度很高。理论切入深入浅出,恰到好处,不牵强且很有说服力。实验部分一来很详尽充实,二来回应了理论部分提出的观点,没有虎头蛇尾,三来在GAN上的表现相信也能提高关注度,能符合很多人的胃口。文末的讨论部分也是写讨论章节的一个很好的范例。
同为ICLR 2018年的投稿,做到同一个点子上的”Data Augmentation by Pairing Samples for Images Classification”这篇文章(已被拒)可以做一个对比。刨去后者在方法上确实有一些缺点,其对比足以说明文章表达能力的差别完全可以让一个点子看起来是一个实实在在的理论贡献,或者只是一个训练的trick。
Reference
[1] V. Vapnik and A. Y. Chervonenkis. On the uniform convergence of relative frequencies of events to their probabilities. Theory of Probability and its Applications, 1971.
[2] C. Zhang, S. Bengio, M. Hardt, B. Recht, and O. Vinyals. Understanding deep learning requires rethinking
generalization. ICLR, 2017.
[3] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. J. Goodfellow, and R. Fergus. Intriguing properties
of neural networks. ICLR, 2014.
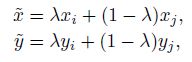
![[深度学习论文笔记][ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION_第1张图片](http://img.e-com-net.com/image/info8/933d0301b0b94d629e82eecfaec4eb23.jpg)
![[深度学习论文笔记][ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION_第2张图片](http://img.e-com-net.com/image/info8/72bca60702a74d8c86594477f6687ce2.jpg)
![[深度学习论文笔记][ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION_第3张图片](http://img.e-com-net.com/image/info8/02c595e0ff6a4bfc868647c04fc1f9ba.jpg)