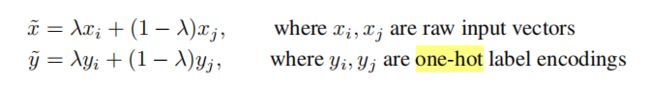论文笔记:mixup: BEYOND EMPIRICAL RISK MINIMIZATION
文章目录
- Abstract
- Introduction
- From ERM to mixup
- Theory
- 一些设计选择与发现
- Mixup做了什么?
- Experiments
- 一些数据集的classification
- Memorization of corrupted labels
- Robustness to adversarial examples
- Stabilization of GANs
- Ablation studies
- 具体实验
- Related work
- Discussion
Abstract
本质上,mixup利用训练样本和他们标签的凸组合训练神经网络
可以对神经网络进行正则化,使其在训练样本之间倾向于简单的线性行为
mixup减少了损坏标签的记忆,提高了对抗示例的鲁棒性,并稳定了GAN的训练。
Introduction
神经网络的两条共性:
- 学习规则是经验风险最小化(ERM)准则,也就是最小化训练数据的平均错误
- SOTA神经网络的规模大小和训练样本数量成线性比例
Motivation:
- 1971年提出的学习理论中的一个经典结果是:只要学习模型的大小不随着训练数据量的增加而增加,ERM的收敛性会得到保证。这样的contradiction使得ERM训练神经网络的合适性被质疑。
- 对抗样本的存在,表明ERM不能解释或者提供在与训练数据分布仅仅有一点区别的测试分布上的泛化性能。
数据增广被认为是一种近邻风险最小化(VRM)准则【在后续会具体涉及介绍】,不过这样的正则手段是依赖于数据集的,因此需要专家知识;另外只是假设近邻样本是相同类别,而并未刻画不同类别的近邻关系(对应到一般数据增广标签不改变)。
Contribution:
通过合并现有的知识(特征向量的线性插值应导致相关目标的线性插值)来扩展训练分布。
实际就是制造虚拟样本和标签
From ERM to mixup
Theory
- empirical risk:
R δ ( f ) = ∫ ℓ ( f ( x ) , y ) d P δ ( x , y ) = 1 n ∑ i = 1 n ℓ ( f ( x i ) , y i ) R_{\delta}(f)=\int \ell(f(x), y) \mathrm{d} P_{\delta}(x, y)=\frac{1}{n} \sum_{i=1}^{n} \ell\left(f\left(x_{i}\right), y_{i}\right) Rδ(f)=∫ℓ(f(x),y)dPδ(x,y)=n1i=1∑nℓ(f(xi),yi)
- vicinal risk:
P ν ( x , y ) = 1 n ∑ i = 1 n ν ( x ~ , y ~ ∣ x i , y i ) R ν ( f ) = 1 m ∑ i = 1 n ℓ ( f ( x ~ i ) , y ~ i ) P_\nu(x,y)=\frac 1 n \sum\limits_{i=1}^n \nu(\tilde x,\tilde y|x_i,y_i) \\ R_\nu(f)=\frac 1 m \sum\limits_{i=1}^n\ell(f(\tilde x_i),\tilde y_i) Pν(x,y)=n1i=1∑nν(x~,y~∣xi,yi)Rν(f)=m1i=1∑nℓ(f(x~i),y~i)
其中 v v v是附近分布,用于测量在训练特征目标对( x i , y i x_i,y_i xi,yi)附近找到虚拟feature-target pairs( x ~ , y ~ \tilde{x},\tilde{y} x~,y~)的可能性。
要学习使用VRM,我们对附近分布进行抽样,以构建数据集 D ν : = ( x ~ i , y ~ i ) i = 1 m \mathcal D_\nu:={(\tilde x_i,\tilde y_i)}_{i=1}^m Dν:=(x~i,y~i)i=1m,并最大程度地减少经验上邻近的风险
举例如高斯近邻: ν ( x ~ , y ~ ∣ x i , y i ) = N ( x ~ − x i , σ 2 ) δ ( y ~ = y i ) \nu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)=\mathcal{N}\left(\tilde{x}-x_{i}, \sigma^{2}\right) \delta\left(\tilde{y}=y_{i}\right) ν(x~,y~∣xi,yi)=N(x~−xi,σ2)δ(y~=yi)
相当于用额外的高斯噪声增广训练数据
- mixup:
μ ( x ~ , y ~ ∣ x i , y i ) = 1 n ∑ j n E λ [ δ ( x ~ = λ ⋅ x i + ( 1 − λ ) ⋅ x j , y ~ = λ ⋅ y i + ( 1 − λ ) ⋅ y j ) ] \mu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)=\frac{1}{n} \sum_{j}^{n} \underset{\lambda}{\mathbb{E}}\left[\delta\left(\tilde{x}=\lambda \cdot x_{i}+(1-\lambda) \cdot x_{j}, \tilde{y}=\lambda \cdot y_{i}+(1-\lambda) \cdot y_{j}\right)\right] μ(x~,y~∣xi,yi)=n1j∑nλE[δ(x~=λ⋅xi+(1−λ)⋅xj,y~=λ⋅yi+(1−λ)⋅yj)]
其中, λ ∼ Beta ( α , α ) \lambda\sim \operatorname{Beta}(\alpha,\alpha) λ∼Beta(α,α),对于任意的 α ∈ ( 0 , ∞ ) \alpha\in(0,\infty) α∈(0,∞)。
mixup中的超参数 α \alpha α控制着特征-目标对插值的强度, α → 0 \alpha \rightarrow 0 α→0时恢复成ERM原则。
一些设计选择与发现
- 在初步实验中,我们发现三个或更多样本的凸组合(利用从Dirichlet分布中采样的权重)不会提供进一步的收益,而且会增加mixup的计算成本。
- 当前的实现使用单个数据加载器来获取一个mini-batch,然后在随机洗牌后将mixup应用到同一mini-batch。效果挺好,且I/O需求降低。
- 仅在具有相等标签的输入之间进行插值并不会导致mixup性能提升。
Mixup做了什么?
作者认为在训练样本之外进行预测时,这种线性行为会减少不期望有的震荡。
同时,线性从奥卡姆的剃刀理论角度,是一个很棒的引导偏向(inductive bias)。
作者绘制了两个图来证实自己的猜想:
图1展示了mixup导致决策边界在类与类之间线性转换,从而提供了更平滑的不确定性估计。
图2展示了利用mixup准则训练出的神经网络相比ERM准则训练出的,在模型预测和训练样本之间的梯度范数上更加稳定。
Experiments
一些数据集的classification
相比ERM准则,分类性能提升
Findings:
- α \alpha α 越大,mixup会导致欠拟合
- 具有更大容量(应该是指模型规模更大吧),更长训练轮数的模型在mixup下收益最大【对比ERM策略】
Memorization of corrupted labels
借鉴Understanding deep learning requires rethinking generalization. ICLR, 2017. 考量对随机损坏标签的鲁棒性
Dropout也是一种SOTA的对付损坏标签的方法,mixup和它是可以结合的
Robustness to adversarial examples
mixup可以通过惩罚沿着最合理的方向(例如到其他训练点的方向)的给定输入的损耗梯度范数来显着提高神经网络的鲁棒性,而不会影响ERM的速度。
Stabilization of GANs
针对情况:判别器经常提供给生成器消失的梯度
作者认为mixup可以使GAN的训练更稳定,因为它可以充当鉴别器梯度的正则化器,类似于二元分类器(后半句有点没懂)
Ablation studies
mixup is a data augmentation method that consists of only two parts: random convex combination of raw inputs, and correspondingly, convex combination of one-hot label encodings.
several design choices
以下对比mixup和一些其他的数据增广可能,如可以选择对神经网络的潜在表示(即特征图)进行插值,并且可以选择仅在最近的邻居之间或仅在相同类别的输入之间进行插值 。
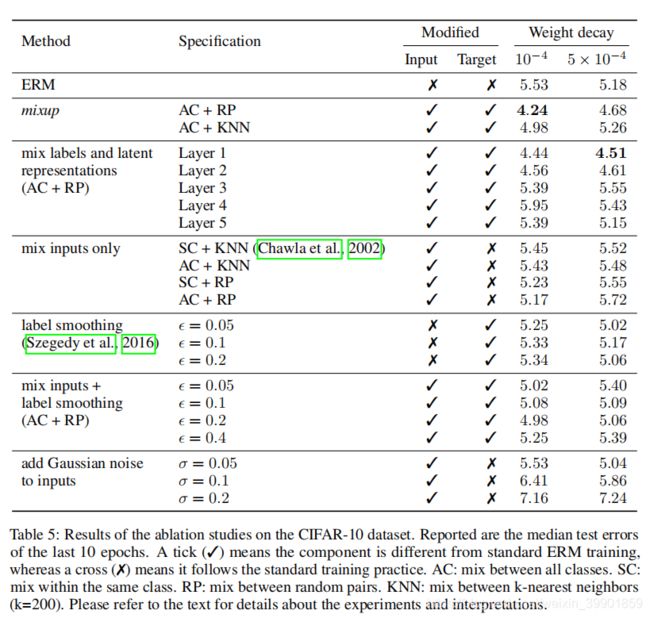
AC: mix between all classes. SC: mix within the same class. RP: mix between random pairs. KNN: mix between k-nearest neighbors (k=200)
以上前两者和后两者可以进行组合搭配。
具体实验
- 比较混合原始输入和混合潜在表示(target都同时进行混合)
- 比较RP和KNN
两组实验:一个是mixup自身,即输入-标签同时混合;另一个是只混合输入。
- 比较混合AC和SC
将小批量与其样本索引的随机排列进行凸组合,其中排列是按per-batch(AC)或每个 per-class(SC)。
- 比较混合输入-标签和只混合输入
要么将两个one-hot编码的凸组合用作目标,要么选择更接近训练样本的one-hot编码作为目标。
结论:
- mixup是最佳数据增广方法,并且效果远好于第二好的(混合输入+平滑标签)【且AC+PR最好】
- 对ERM而言,更大的权重衰减系数会使test error变小;而对mixup而言,更小的权重衰减系数更有利,证明了mixup的正则化效果。
Related work
- 数据增广:在所有情况下,都将充分利用领域知识来设计合适的数据转换,从而提高通用性。
有一些类似方法:在监督方面取决于多个平滑标签,而不是像传统ERM中那样取决于单个硬标签,在某种意义上说,它们与mixup具有相似性。但是如label smoothing,正则是独立于输入的。
mixup变换在数据增强和监督信号之间建立了线性关系。作者通过实验证实,这将导致强大的正则化效果,从而提高泛化能力。
Discussion
mixup通过超参 α \alpha α, 隐式提升了模型复杂度:当 α \alpha α变大,训练错误率提升,但是generalization gap缩小。
但是目前没有一个好的理论理解这样一种偏差-方差权衡的“最佳点”,作者推测模型容量会使得训练错误对大的 α \alpha α更不敏感,那这是mixup的一个更棒的优势。
Further exploration:
- similar ideas在其他种类的监督任务上,如回归,结构化预测等?
- beyond监督任务?(作者认为这种interpolation principle看起来是一种合理的inductive bias,可能对无监督,半监督【MixMatch证实了这点】,强化学习有帮助)
- 是否可以将mixup扩展到feature-label外推,以确保远离训练数据的鲁棒模型行为?