机器人工具箱实战

目的：

取一条腿为研究对象，对单腿的原地踏步进行模拟与仿真，给出运动轨迹，并得到相应的关节角的运动参数
后续想法->编写函数，输入轨迹，输出运动参数：

过程与实现：

创建单腿模型

L(1)=Link([0,0,0,pi/2]);
L(2)=Link([0,0,1,0]);
L(3)=Link([0,0,1,0]);
L(4)=Link([0,0,0,pi/2]);
L(5)=Link([0,0,0,0]);
L(6)=Link([0,0,0,0]);
two_link=SerialLink(L,'name','twolink');

其中1456是为了使用内置函数而设置的冗余自由度，对于该模拟无影响

期望运动轨迹：

位姿状态T1：

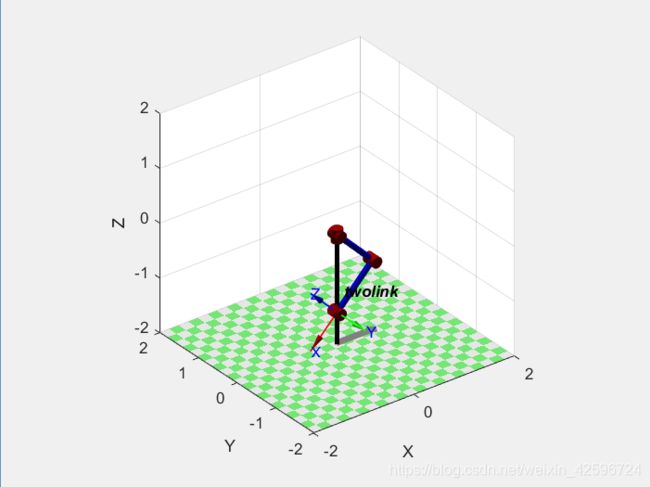
位姿状态T2：

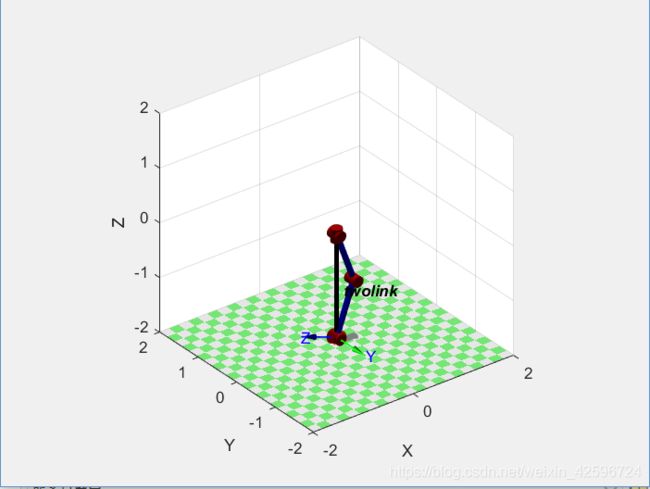
键入初始和结束关节角并得到变化矩阵：

qn=[0,-pi/4,-pi/2,0,0,0];
q1=[0,-70/180*pi,-40/180*pi,0,0,0];
T1=two_link.fkine(qn);
T2=two_link.fkine(q1);

设置末端执行器从T1状态移动到T2状态，用时1s，每100ms计算一次关节角

t=[0:0.1:1];

计算：

[q v a]=jtraj(qn,q1,t);  %%该函数默认将始末位置的速度加速度取0或趋于0

q=
0	-0.785398163397448	-1.57079632679490	0	0	0
0	-0.789133167996716	-1.56332631759636	0	0	0
0	-0.810670530966326	-1.52025159165714	0	0	0
0	-0.856555237001257	-1.42848217958728	0	0	0
0	-0.923907492835718	-1.29377766791836	0	0	0
0	-1.00356431989674	-1.13446401379631	0	0	0
0	-1.08322114695776	-0.975150359674272	0	0	0
0	-1.15057340279222	-0.840445848005349	0	0	0
0	-1.19645810882715	-0.748676435935486	0	0	0
0	-1.21799547179676	-0.705601709996267	0	0	0
0	-1.22173047639603	-0.698131700797730	0	0	0

令s1为关节1(q中的第二列)所记录的关节角矩阵,同理得s2：

s1=q(:,2)';
s2=q(:,3)';

三次多形式拟合

p1=polyfit(t,s1,3);
p2=polyfit(t,s2,3);

f1=polyval(p1,t);
f2=polyval(p2,t);
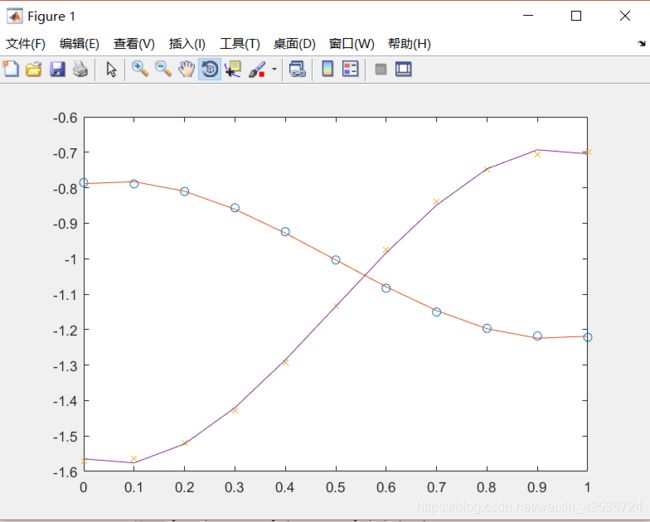
plot(t,s1,'o',t,f1,t,s2,'x',t,f2) ;

得到曲线：

p1 =

    1.3526   -2.0289    0.2463   -0.7885

p2 =

   -2.7053    4.0579   -0.4925   -1.5645

我们可以得到关节1和关节2的三次多项式：
$${\theta }_1=1.3526t^3-2.0289t^2+0.2463t-0.7885$$
$${\theta }_2=-2.7053t^3+4.0579t^2-0.4925t-1.5645$$
以上是比较特殊的情况，接下来将讨论更为一般的情况
实际上只要能给出末端执行器的位姿随时间的变化，我们就能得到各关节的运动参数