机器人动力学(牛顿欧拉推导)
刚体加速度
分析刚体加速度时,在任一顺势瞬时,对刚体的线速度和角速度进行求导,可以分别得到线加速度和角加速度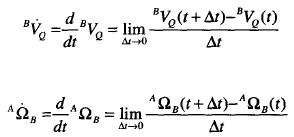
线加速度
根据前一章推导得到的,坐标系{A}下的速度矢量 B Q ^BQ BQ
当坐标系{A}的原点与坐标系{B}重合时,速度矢量 B Q ^BQ BQ可表示为: A V Q = B A R B V Q + A Ω B × A Q ^{A}\textrm{V}_{Q}=^A_BR^BV^Q+^{A}\Omega_B\times^{A}\textrm{Q} AVQ=BARBVQ+AΩB×AQ (1)
将左侧求导改写为:
d d t ( A V Q ) = B A R B V Q + A Ω B × A Q \frac {d} {dt}(^{A}\textrm{V}_{Q})=^A_BR^BV^Q+^{A}\Omega_B\times^{A}\textrm{Q} dtd(AVQ)=BARBVQ+AΩB×AQ(2)
对式(1)求导,可得当坐标系{A}和坐标系{B}原点重合时, B Q ^BQ BQ的加速度在坐标系{A}中的表达式:
A V Q ˙ = d d t ( B A R B V Q ) + A Ω B ˙ × B A R B Q + A Ω B × d d t ( B A R B Q ) \dot{^{A}\textrm{V}_{Q}}=\frac {d} {dt}(^A_BR^BV^Q)+\dot{^{A}\Omega_B}\times^A_BR^BQ+^{A}\Omega_B\times\frac{d}{dt}(^A_BR^BQ) AVQ˙=dtd(BARBVQ)+AΩB˙×BARBQ+AΩB×dtd(BARBQ)(3)
将(3)式右侧的第一项和最后一项带入式(2)中,整理后可得:
A V Q ˙ = B A R B V Q ˙ + 2 A Ω B × B A R B V Q + A Ω B ˙ × B A R B Q + A Ω B × ( A Ω B × B A R B Q ) \dot{^{A}\textrm{V}_{Q}}=^A_BR\dot{^BV_Q}+2^{A}\Omega_B\times^A_BR^{B}\textrm{V}_Q+\dot{^{A}\Omega_B}\times^A_BR^BQ+^{A}\Omega_B\times({^{A}\Omega_B}\times^A_BR^BQ) AVQ˙=BARBVQ˙+2AΩB×BARBVQ+AΩB˙×BARBQ+AΩB×(AΩB×BARBQ)(4)
将上式扩展到原点不重合的情况,即可得到一般表达式:
A V Q ˙ = A V ˙ B O G R + B A R B V Q ˙ + 2 A Ω B × B A R B V Q + A Ω B ˙ × B A R B Q + A Ω B × ( A Ω B × B A R B Q ) \dot{^{A}\textrm{V}_{Q}}=\dot{^A\textrm{V}}_{BOGR}+^{A}_{B}\textrm{R}\dot{^BV_Q}+2^{A}\Omega_B\times^A_BR^{B}\textrm{V}_Q+\dot{^{A}\Omega_B}\times^A_BR^BQ+^{A}\Omega_B\times({^{A}\Omega_B}\times^A_BR^BQ) AVQ˙=AV˙BOGR+BARBVQ˙+2AΩB×BARBVQ+AΩB˙×BARBQ+AΩB×(AΩB×BARBQ)(5)
当计算为旋转关节时, B Q ^BQ BQ为常量,有:
B V Q = B V ˙ Q = 0 ^BV_Q=^B\dot{V}_Q=0 BVQ=BV˙Q=0
上式可化简为: A V Q ˙ = A V ˙ B O G R + A Ω B ˙ × B A R B Q + A Ω B × ( A Ω B × B A R B Q ) \dot{^{A}\textrm{V}_{Q}} = \dot{^A\textrm{V}}_{BOGR}+\dot{^{A}\Omega_B}\times^A_BR^BQ+^{A}\Omega_B\times({^{A}\Omega_B}\times^A_BR^BQ) AVQ˙=AV˙BOGR+AΩB˙×BARBQ+AΩB×(AΩB×BARBQ)(6)
角加速度
假设坐标系{B}以角速度 A Ω B ^A\Omega_B AΩB相对于坐标系{A}转动,同时坐标系{C}以角速度 B Ω C ^B\Omega_C BΩC相对于坐标系{B}转动,为了求 A Ω C ^A\Omega_C AΩC在坐标系{A}中进行矢量相加
A Ω C = A Ω B + B A R B Ω C ^A\Omega_C=^A\Omega_B+^A_BR^B\Omega_C AΩC=AΩB+BARBΩC (7)
对(7)求导可以有: A Ω C ˙ = A Ω B ˙ + B A R B Ω ˙ C + B A R B Ω C \dot{^A\Omega_C}=\dot{^A\Omega_B}+^A_BR^B\dot{\Omega}_C+^A_BR^B\Omega_C AΩC˙=AΩB˙+BARBΩ˙C+BARBΩC(8)
将式(2)带入可以有:
A Ω C ˙ = A Ω B ˙ + B A R B Ω ˙ C + A Ω B × B A R B Ω C \dot{^A\Omega_C}=\dot{^A\Omega_B}+^A_BR^B\dot{\Omega}_C+^A\Omega_B\times^A_BR^B\Omega_C AΩC˙=AΩB˙+BARBΩ˙C+AΩB×BARBΩC(9)
利用式(9)可以计算机器人连杆的角加速度
质量分布
对于定州转动的情况,经常用到惯性矩阵的概念,为了表征刚体质量分布的方式,这里引入惯性张量,可以看做对一个物体惯性矩的广义度量。
给出 3 × 3 3\times3 3×3矩阵:
A I = [ I x x − I x y − I x z − I x y I y y − I y z − I x z − I y z I z z ] ^AI=\begin{bmatrix} I_{xx}& -I_{xy} &-I_{xz} \\ -I_{xy}& I_{yy} & -I_{yz}\\ -I{xz}& -I_{yz} & I_{zz} \end{bmatrix} AI=⎣⎡Ixx−Ixy−Ixz−IxyIyy−Iyz−Ixz−IyzIzz⎦⎤
其中各个元素分别为:

刚体由单元体 d v dv dv组成,单元体的密度是 ρ \rho ρ,每个单元体的位置矢量由矢量 A P = [ x y z ] T ^AP=[xyz]^T AP=[xyz]T确定。其中 I x x , I y y , I z z I_{xx} ,I_{yy}, I_{zz} Ixx,Iyy,Izz称为惯量距,其余三个交叉项称为惯量积,对于一个刚体来讲,这六个相互独立的参量取决于所在坐标系的位姿
注:惯量距永远是正直,而惯量积则有可能是正值或负值
不论参考坐标系方位如何变化,三个惯量距的和保持不变。
平行移轴定理
由于实际应用中,质心位置必然不会和坐标系重合,所以需要用到平行移轴定理将以刚体质心为原点的坐标系平移到运动学坐标系
此处定义质心坐标系为{G},运动学坐标系为{O}
对于刚体质心坐标系{G}刚体惯性张量 I I I可以表示为:
A I = [ I x x − I x y − I x z − I x y I y y − I y z − I x z − I y z I z z ] ^AI=\begin{bmatrix} I_{xx}& -I_{xy} &-I_{xz} \\ -I_{xy}& I_{yy} & -I_{yz}\\ -I{xz}& -I_{yz} & I_{zz} \end{bmatrix} AI=⎣⎡Ixx−Ixy−Ixz−IxyIyy−Iyz−Ixz−IyzIzz⎦⎤
质心{G}相对于{O}的位置为: ( x , y , z ) (x,y,z) (x,y,z)
则根据平行轴定理有对于{O}的惯性张量为:
I x x = I G x x + m ( y 2 + z 2 ) I_{xx}=I_{Gxx}+m(y^2+z^2) Ixx=IGxx+m(y2+z2)
I y y = I G y y + m ( x 2 + z 2 ) I_{yy}=I_{Gyy}+m(x^2+z^2) Iyy=IGyy+m(x2+z2)
I z z = I G z z + m ( x 2 + y 2 ) I_{zz}=I_{Gzz}+m(x^2+y^2) Izz=IGzz+m(x2+y2)
I x y = I y x = I G x y + m x y I_{xy}=I_{yx}=I_{Gxy}+mxy Ixy=Iyx=IGxy+mxy
I x z = I z x = I G x z + m x z I_{xz}=I_{zx}=I_{Gxz}+mxz Ixz=Izx=IGxz+mxz
I y z = I z y = I G y z + m y z I_{yz}=I_{zy}=I_{Gyz}+myz Iyz=Izy=IGyz+myz
牛顿欧拉方程
把机器人的连杆都看做是刚体,如果知道连杆质心的位置和惯性张量,那么他的质量分布特征就完全确定了,要让连杆运动,必须对连杆进行加速和减速,连杆运动所需要的力是关于连杆期望加速度及其质量分布的函数。牛顿欧拉方程描述了力、惯量和加速度之间的联系
牛顿方程
刚体质心以加速度 v ˙ C \dot{v}_C v˙C作加速运动,有牛顿方程可以得到作用在质心上的力F引起的刚体加速度: F = m v ˙ C F=m\dot{v}_C F=mv˙C
欧拉方程
对于旋转刚体,角速度和角加速度分别为 ω , ω ˙ \omega,\dot{\omega} ω,ω˙,由欧拉方程可有: N = C I ω ˙ + ω × C I ω N=^CI\dot{\omega}+\omega\times^CI\omega N=CIω˙+ω×CIω,其中 C I ^CI CI是刚体在坐标系{C}中的惯性张量,坐标系{C}的原点在刚体质心
牛顿欧拉地推动力学方程
就是假设已知关节的位置、速度、加速度( Θ , Θ ˙ , Θ ¨ \Theta,\dot{\Theta},\ddot{\Theta} Θ,Θ˙,Θ¨),结合前边的运动学和质量分布,计算出驱动关节运动所需要的力矩,此算法主要包括三步:
1、计算速度和加速度外推法
2、分别运用牛顿方程和欧拉方程,计算作用在连杆质心上的惯性力和力矩
3、计算力和力矩的内推法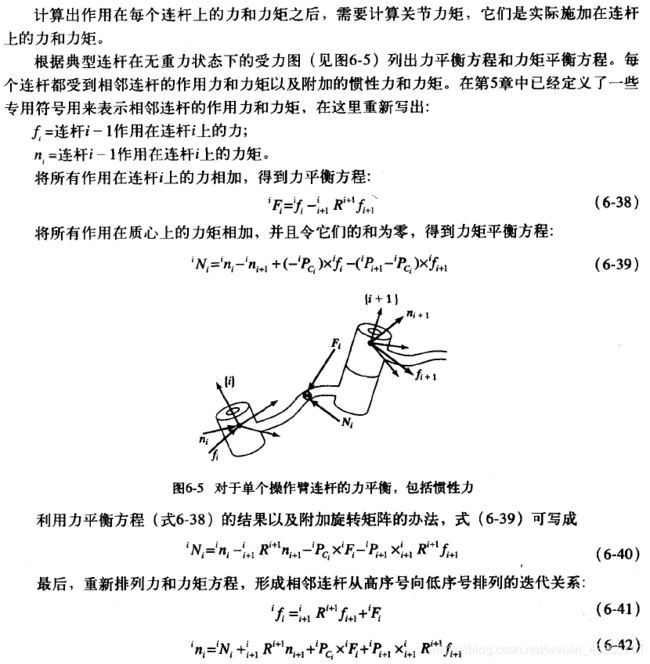

最终算法可归纳为:
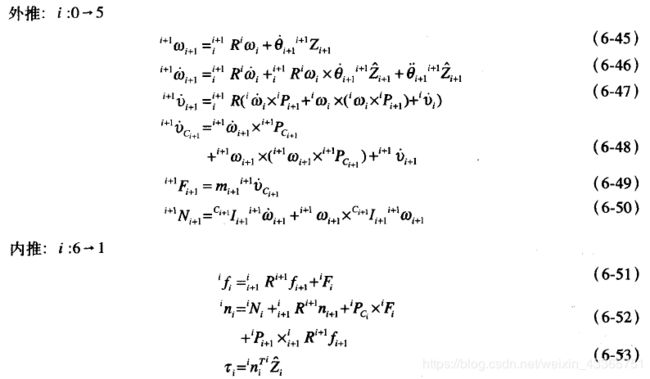
注:令 0 v ˙ 0 = G ^0\dot{v}_0=G 0v˙0=G就可以简单的将作用在连杆上的重力因素包括到动力学方程中去,G与重力矢量大小相等,方向相反
状态空间方程
动力学方程可以表示为:
τ = M ( Θ ) Θ ˙ + V ( Θ , Θ ˙ ) + G ( Θ ) \tau=M(\Theta)\dot{\Theta}+V(\Theta,\dot{\Theta})+G(\Theta) τ=M(Θ)Θ˙+V(Θ,Θ˙)+G(Θ)
其中 M ( Θ ) M(\Theta) M(Θ)为机器人 n × n n\times n n×n质量矩阵, V ( Θ , Θ ˙ ) V(\Theta,\dot{\Theta}) V(Θ,Θ˙)是 n × 1 n\times 1 n×1的离心力和哥氏力矢量, G ( Θ ) G(\Theta) G(Θ)是重力矢量
形位空间方程
将动力学方程中的速度项 V ( Θ , Θ ˙ ) V(\Theta,\dot{\Theta}) V(Θ,Θ˙)写成另一种形式:
τ = M ( Θ ) Θ ¨ + B ( Θ ) [ Θ ˙ Θ ] ˙ + C ( Θ ) [ Θ 2 ˙ ] + G ( Θ ) \tau=M(\Theta)\ddot{\Theta}+B(\Theta)[\dot{\Theta}\dot{\Theta]}+C(\Theta)[\dot{\Theta^2}]+G(\Theta) τ=M(Θ)Θ¨+B(Θ)[Θ˙Θ]˙+C(Θ)[Θ2˙]+G(Θ)

总结
由于通常计算机计算中,考虑计算效率问题,牛顿欧拉法比拉格朗日法用的多,所以此处就暂时不对拉格朗日法进行整理和总结了