LSNU寒假集训 题解
目录
LSNU寒假第一场(基础算法+几何)
A - Fifa and Fafa
B - Anton and Lines
C - Minimum path
D - Thematic Contests
E - Balanced Playlist
F - Median String
G - String Reconstruction
H - Palindrome Pairs
LSNU寒假第二场(动态规划)
A - Vitamins
B - Polycarp and Div 3
LSNU寒假第三场(数据结构)
A - A and B and Compilation Errors
B - Maximum Absurdity
C - Contest Balloons
D - Dense Subsequence
E - Kostya the Sculptor
LSNU寒假第四场(图论+搜索)
A - Cyclic Components
B - Fight Against Traffic
C - Love Rescue
LSNU寒假第五场(数论)
A - The Wall (medium)
B - Selection of Personnel
C - New Year and the Sphere Transmission
D - Social Circles
E - Enlarge GCD
G - Remainders Game
LSNU寒假第一场(基础算法+几何)
比赛传送门
A - Fifa and Fafa
Fifa and Fafa are sharing a flat. Fifa loves video games and wants to download a new soccer game. Unfortunately, Fafa heavily uses the internet which consumes the quota. Fifa can access the internet through his Wi-Fi access point. This access point can be accessed within a range of r meters (this range can be chosen by Fifa) from its position. Fifa must put the access point inside the flat which has a circular shape of radius R. Fifa wants to minimize the area that is not covered by the access point inside the flat without letting Fafa or anyone outside the flat to get access to the internet.
The world is represented as an infinite 2D plane. The flat is centered at (x1, y1) and has radius R and Fafa's laptop is located at (x2, y2), not necessarily inside the flat. Find the position and the radius chosen by Fifa for his access point which minimizes the uncovered area.
Input
The single line of the input contains 5 space-separated integers R, x1, y1, x2, y2 (1 ≤ R ≤ 105, |x1|, |y1|, |x2|, |y2| ≤ 105).
Output
Print three space-separated numbers xap, yap, r where (xap, yap) is the position which Fifa chose for the access point and r is the radius of its range.
Your answer will be considered correct if the radius does not differ from optimal more than 10 - 6 absolutely or relatively, and also the radius you printed can be changed by no more than 10 - 6 (absolutely or relatively) in such a way that all points outside the flat and Fafa's laptop position are outside circle of the access point range.
Examples
Input
5 3 3 1 1
Output
3.7677669529663684 3.7677669529663684 3.914213562373095
Input
10 5 5 5 15
Output
5.0 5.0 10.0题意:
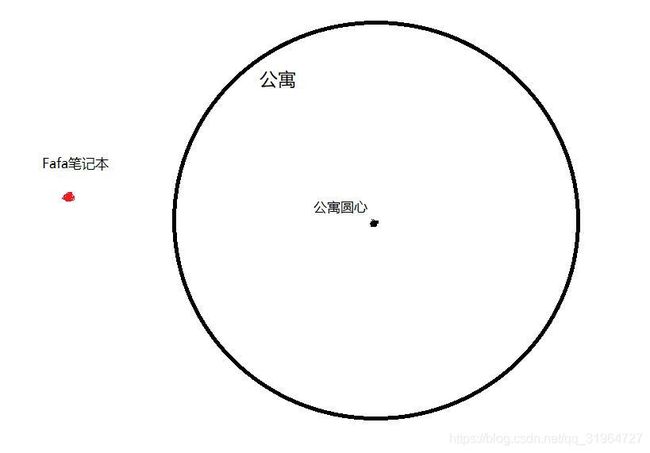
Fifa和Fafa共用一间公寓。Fifa喜欢电子游戏,想下载一款新的足球游戏。不幸的是,Fafa大量使用互联网,消耗了所有配额。Fifa可以通过他的WiFi接入点上网。这个接入点使附近 r 米范围内可连上网络(这个范围 r 的大小可以由Fifa选择)。Fifa必须将接入点设置在半径为 R 的圆形公寓内。Fifa希望在不让Fafa或公寓外的任何人接入互联网的情况下,将接入点未覆盖的区域最小化。
世界被表示为一个无限的二维平面。公寓以(x1, y1)为中心,半径为R, Fafa的笔记本电脑位于(x2, y2),不一定在公寓内。找到Fifa为他的接入点所选择的位置和半径,使得未覆盖的区域最小化。
总结题意就是Fifa要在这个圆形的公寓内放置一个wifi,wifi有摆放位置和可自定义的信号半径,这个描述wifi范围的圆要尽可能大以覆盖公寓中更多区域,却又不能将Fafa的笔记本包进来(避免Fafa连上),更不能超出公寓范围(避免公寓外的人连上),输出最优的wifi的摆放位置和信号半径,且结果误差要在1e-6以内.
思路:
其实影响wifi摆放位置与信号半径的只有Fafa的笔记本和公寓,问题情况基于笔记本和公寓的关系分两种:
1.当笔记本在公寓外时,wifi摆放在公寓正中心,信号半径和公寓半径相同自然就是最优.
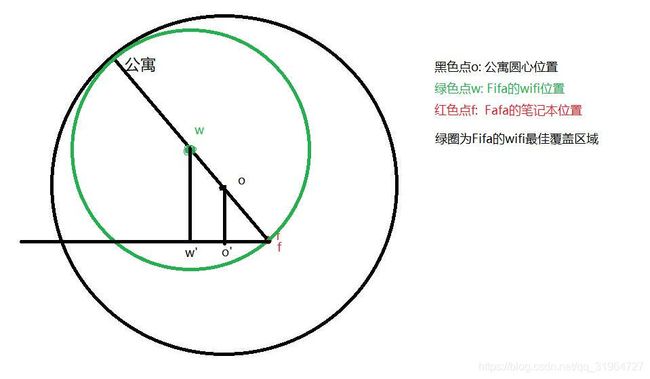
2.当笔记本在公寓内且不在公寓圆心时,wifi摆放在笔记本与公寓圆心所成直线上才可得到最大信号半径如图,此时wifi的信号半径r=(R+dis(公寓圆心,Fafa笔记本))/2 ,至于wifi圆心的摆放位置可以通过相似三角形快速得到.即三角形foo'与fww'相似,故而:
故而wifi摆放位置相对于f点的x轴差值为fw'=fw*fo'/fo,已知f(x1,y1)与o(x2,y2)带入方程即可得到wifi摆放位置的x坐标
故而wifi摆放位置相对于f点的y轴差值为ww'=fw*oo'/fo,已知f(x1,y1)与o(x2,y2)带入方程即可得到wifi摆放位置的y坐标
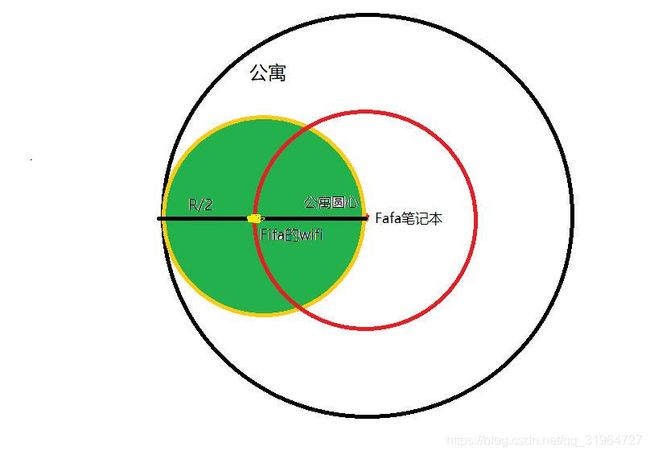
3.当笔记本在公寓圆心时,此时的最大信号半径确定为R/2,而圆心位置可以在图中红圈上的任意一点
AC代码:
#include
#include
struct point{
double x,y;
};
// 求两点距离
double get_two_point_dis(const point &a,const point &b){
return sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2));
}
const double eps=1e-6; // 精度
// 比较两浮点数大小,相等返回0,ab返回-1
int float_compare(const double &a,const double &b){
if(fabs(a-b) B - Anton and Lines
The teacher gave Anton a large geometry homework, but he didn't do it (as usual) as he participated in a regular round on Codeforces. In the task he was given a set of n lines defined by the equations ![]() . It was necessary to determine whether there is at least one point of intersection of two of these lines, that lays strictly inside the strip between
. It was necessary to determine whether there is at least one point of intersection of two of these lines, that lays strictly inside the strip between ![]() . In other words, is it true that there are 1 ≤ i < j ≤ n and x', y', such that:
. In other words, is it true that there are 1 ≤ i < j ≤ n and x', y', such that:
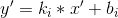 , that is, point (x', y') belongs to the line number i;
, that is, point (x', y') belongs to the line number i;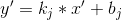 , that is, point (x', y') belongs to the line number j;
, that is, point (x', y') belongs to the line number j;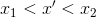 , that is, point (x', y') lies inside the strip bounded by
, that is, point (x', y') lies inside the strip bounded by 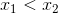 .
.
You can't leave Anton in trouble, can you? Write a program that solves the given task.
Input
The first line of the input contains an integer n (2 ≤ n ≤ 100 000) — the number of lines in the task given to Anton. The second line contains integers ![]() and
and ![]() ( - 1 000 000 ≤
( - 1 000 000 ≤ ![]() <
< ![]() ≤ 1 000 000) defining the strip inside which you need to find a point of intersection of at least two lines.
≤ 1 000 000) defining the strip inside which you need to find a point of intersection of at least two lines.
The following n lines contain integers ![]() ,
, ![]() ( - 1 000 000 ≤
( - 1 000 000 ≤ ![]() ,
, ![]() ≤ 1 000 000) — the descriptions of the lines. It is guaranteed that all lines are pairwise distinct, that is, for any two i ≠ j it is true that either
≤ 1 000 000) — the descriptions of the lines. It is guaranteed that all lines are pairwise distinct, that is, for any two i ≠ j it is true that either ![]() , or
, or ![]() .
.
Output
Print "Yes" (without quotes), if there is at least one intersection of two distinct lines, located strictly inside the strip. Otherwise print "No" (without quotes).
Examples
Input
4
1 2
1 2
1 0
0 1
0 2
Output
NOInput
2
1 3
1 0
-1 3
Output
YESInput
2
1 3
1 0
0 2
Output
YESInput
2
1 3
1 0
0 3
Output
NONote
In the first sample there are intersections located on the border of the strip, but there are no intersections located strictly inside it.
题意:
老师给安东布置了大量的几何作业,但他没有(像往常一样)去做,因为他参加了一个常规的Codeforces测试。在这个任务中,他得到了由方程 ![]() 定义的n条直线。必须确定这两条直线之间是否存在至少一个交点 (x',y'),该交点严格位于
定义的n条直线。必须确定这两条直线之间是否存在至少一个交点 (x',y'),该交点严格位于![]() 之间的带状区域内。也就是说,是否存在1 ≤ i < j ≤ n, x', y',使得:
之间的带状区域内。也就是说,是否存在1 ≤ i < j ≤ n, x', y',使得:
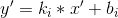 , 即点(x', y')属于第i条直线;
, 即点(x', y')属于第i条直线;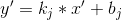 , 即点(x', y')属于第j条直线;
, 即点(x', y')属于第j条直线;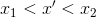 , 即点(x', y')位于以
, 即点(x', y')位于以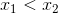 为界的带状区域内。
为界的带状区域内。
你不能丢下安东不管,对吧?编写一个程序来解决给定的任务。
总结题意就是给你n(1e5以内)条直线(输入保证没有相同直线),以及![]() ,问这n条线段是否存在任意两条直线的交点正好在
,问这n条线段是否存在任意两条直线的交点正好在![]() 以内,注意是开区间因为题目要求严格在此区间内.
以内,注意是开区间因为题目要求严格在此区间内.
思路:
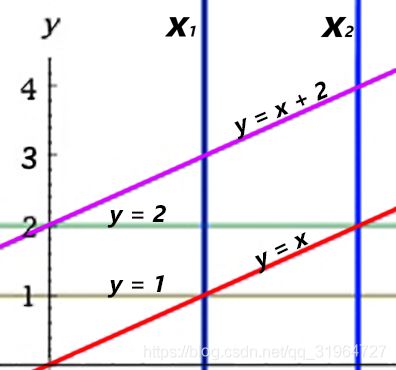
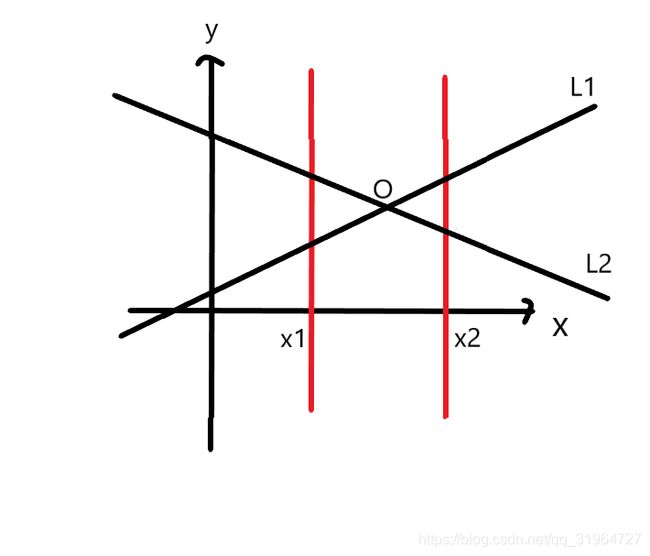
首先因为数据量级达到1e5导致暴力枚举所有直线交点判断是否在![]() 以内会TLE,故而我们转变思路研究相交的情况有什么特别之处.如图直线L1与直线L2相交于x=x1与x=x2之间的点O
以内会TLE,故而我们转变思路研究相交的情况有什么特别之处.如图直线L1与直线L2相交于x=x1与x=x2之间的点O
此时可以发现相交的L1与L2关于x=x1,x=x2的交点在y方向上是顺序相反的,而反之不存在交点或者交点在外面时,关于x=x1,x=x2的交点在y方向上顺序必然相同.故而可以通过这一点判断两直线是否存在![]() 以内的交点.
以内的交点.
其次若如图L1L2相交的情况下,L1交x=x1于B,L2交x=x1于A,若存在直线L3与x=x1交于A B之间的点C,我们可知此时L3必与L1或L2相交,因此若存在任意两相交直线,则必然存在两相交直线与x=x1的交点在所有n个交点中满足相邻
通过以上两个加粗的关键点我们可以开始编写算法,先预处理出n条直线与x=x1与x=x2的交点并根据与x=x1的交点y值排序(y值相同时根据与x=x2的交点y值排序),升序降序无所谓
根据排序得到的n条直线的顺序依次比较相邻的2条直线与x=x1和x=x2的交点y值,判断是否满足相反,满足相反的那一对相邻直线必相交
AC代码:
#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll inf=1e14;
// 直线结构体 y=kx+b
struct line{
ll k,b;
}li[maxn];
// 某条直线与x=x1相交于first,与x=x2相交于second
pair inters[maxn];
int sign(ll t){
if(t>0) return 1;
else if(t<0) return -1;
return 0;
}
void solve(){
int n;
scanf("%d",&n);
int x1,x2;
scanf("%d%d",&x1,&x2);
for(int i=0;i C - Minimum path
You are given a matrix of size n×n filled with lowercase English letters. You can change no more than k letters in this matrix.
Consider all paths from the upper left corner to the lower right corner that move from a cell to its neighboring cell to the right or down. Each path is associated with the string that is formed by all the letters in the cells the path visits. Thus, the length of each string is 2n−1.
Find the lexicographically smallest string that can be associated with a path after changing letters in at most k cells of the matrix.
A string a is lexicographically smaller than a string b, if the first different letter in a and b is smaller in a .
Input
The first line contains two integers n and k (1≤n≤2000, 0≤k≤n2 ) — the size of the matrix and the number of letters you can change.
Each of the next n lines contains a string of n lowercase English letters denoting one row of the matrix.
Output
Output the lexicographically smallest string that can be associated with some valid path after changing no more than k letters in the matrix.
Examples
Input
4 2
abcd
bcde
bcad
bcde
Output
aaabcde
Input
5 3
bwwwz
hrhdh
sepsp
sqfaf
ajbvw
Output
aaaepfafw
Input
7 6
ypnxnnp
pnxonpm
nxanpou
xnnpmud
nhtdudu
npmuduh
pmutsnz
Output
aaaaaaadudsnz
Note
In the first sample test case it is possible to change letters 'b' in cells (2,1) and (3,1) to 'a', then the minimum path contains cells (1,1),(2,1),(3,1),(4,1),(4,2),(4,3),(4,4). The first coordinate corresponds to the row and the second coordinate corresponds to the column.
题意:
你有一个大小为n×n的方阵,里面全是小写的英文字母。你最多只能改变这个方阵中的 k 个字母。
考虑从左上角到右下角的所有路径,这些路径从一个单元格移动到相邻的单元格,只能移动到右边或下边相邻单元格。每个路径用依次经过的单元格中的字母组成的字符串表示。因此,每个路径字符串的长度是2n - 1.
寻找改变最多k个单元格中的字符后能得到的字典序最小的路径字符串,
一个字符串a的字典序比字符串b的字典序小,当且仅当ab中第一个不相同的字符是a中更小时.
总结题意就是给你一个n*n的字母方阵,你能改变这个方阵中最多k个字母,然后以左上角为起点,右下角为终点,且只能向右或者向下走,问你所有路径中字典序最小的是哪条路径.
思路:
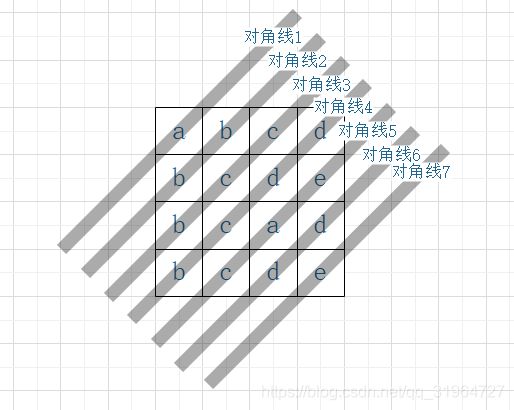
首先如果仅仅是给我们一个字母方阵,只能向右下走,要找左上角到右下角的最小字典序路径是很简单的,因为只能向右下走这一条件很关键,这决定了(0,0)到(n-1,n-1)路径长度必为2*n-1,而其第i步一定在第i条对角线上,且由于是最小字典序,我们的情况求解是贪心的.
故而我们只需要对这2*n-1条对角线从左上到右下依次找对角线上的相连的最小字符即可,而这体现的也正是bfs的核心思想,从近到远依次遍历所有状态,故而这里可以通过写循环扫描对角线实现也可以通过bfs实现.
然而问题没那么简单,加了条件可以改变方阵中k个字母之后我们无法直接贪心了,因为比如baaaa字典序大于azzzz可是如果允许改变一个字符我们把b改成a则aaaaa毫无疑问的大于azzzz的任何改法,故而我们要设法统计k次修改能造成的变动
毕竟是字典序,谁的前缀a多谁小,故而我们实际上是要使用k次修改修改出前缀a个数尽可能多的路径字符串,其实就是一种dp最优解,问题初始状态可描述为:在(0,0)点前缀全a剩余k个改变权,故设计dp[i][j]含义如下:
- dp[i][j]大于等于0时表示从(0,0)到(i,j)的所有路径字符串中开挂使得全部变为'a'之后最大的剩余改变权个数
- dp[i][j]小于0时表示从(0,0)到(i,j)的所有路径字符串中开挂后前缀a最多的那个字符串除去前缀a之后的长度*-1
而转移方程: dp[i][j]=max(dp[i-1][j]-(dp[i-1][j]<0||lm[i-1][j]!='a'),dp[i][j-1]-(dp[i][j-1]<0||lm[i][j-1]!='a')) (0<=i,j 就这样一直转移到dp[n-1][n-1]为止,最后dp值为-1的自然就是前缀a紧接着的位置,取离终点距离最近的-1即可.因为距离终点最近说明前缀a最多,自然是用完k个改变权之后字典序最小的,这样k个改变权的影响就不复存在了,对距离终点最近的-1按照之前的对角线扫描或者bfs做就好. Polycarp has prepared n competitive programming problems. The topic of the i-th problem is Polycarp has to host several thematic contests. All problems in each contest should have the same topic, and all contests should have pairwise distinct topics. He may not use all the problems. It is possible that there are no contests for some topics. Polycarp wants to host competitions on consecutive days, one contest per day. Polycarp wants to host a set of contests in such a way that: Your task is to calculate the maximum number of problems in the set of thematic contests. Note, that you should not maximize the number of contests. The first line of the input contains one integer n ( The second line of the input contains n integers Print one integer — the maximum number of problems in the set of thematic contests. In the first example the optimal sequence of contests is: 2 problems of the topic 1, 4 problems of the topic 2, 8 problems of the topic 10. In the second example the optimal sequence of contests is: 3 problems of the topic 3, 6 problems of the topic 6. In the third example you can take all the problems with the topic 1337 (the number of such problems is 3 so the answer is 3) and host a single contest. Polycarp准备了n个用于比赛的编程问题。第i个问题的主题是 Polycarp将要举办一些主题竞赛。每一场比赛的所有问题都应该有相同的主题,所有的比赛都应该有两两不同的主题。他可能不会利用所有的问题。有些主题可能没有竞赛。 Polycarp希望连续举办比赛,每天一场。Polycarp希望以这样的方式举办一系列比赛: 你的任务是计算一组主题竞赛中问题的最大数量。注意,您不应该最大化竞赛的数量。 总结题意就是Polycarp有n个问题,每个问题有类型(可能重复),(topic就好像动态规划类型,搜索类型,数论类型,计算几何类型...),现在基于这些问题一天一场举办任意多场主题不重复的比赛,每场比赛问题数目是上场的2倍,且每场比赛主题不重复,问你所有竞赛的问题总数最大的举办方式能包含多少道问题. 由于问题总数n是在2e5以内,故而我们可知任意一种主题问题的总数不会超过n,题目无非是要找一个比为2的等比数列,由于单种问题数目在2e5以内故而我们可以估计这个等比数列的项数不超过18个. 知道了这些信息之后我们可以考虑枚举这个等比数列的起点,然后检查其每一项是否存在某个对应种类问题即可,而检查可以通过预处理所有种类问题数目并排序后使用二分查找 最后进行复杂度分析,空间上只需要一个map用于问题分类统计,一个n大小数组用于各种类问题数目记录.而时间复杂度上,由于单种问题数目在2e5以内,故而起点枚举复杂度最高2e5,而项数最多18个,每一项的检查通过二分效率在logm(m是问题种数),总复杂度n*18*logm左右,看似容易爆,然而枚举起点的n是指所有种类问题中数目最大的问题数目,并非完全的2e5的n,除非全部问题都是同一种类.而logm的m也非2e5而是问题种数,除非全部问题都是不同种类,故而n与logm总有一个会偏小,总体效率可行. Your favorite music streaming platform has formed a perfectly balanced playlist exclusively for you. The playlist consists of n tracks numbered from 1 to n. The playlist is automatic and cyclic: whenever track i finishes playing, track i+1 starts playing automatically; after track n goes track 1. For each track i, you have estimated its coolness Every morning, you choose a track. The playlist then starts playing from this track in its usual cyclic fashion. At any moment, you remember the maximum coolness x of already played tracks. Once you hear that a track with coolness strictly less than For each track i , find out how many tracks you will listen to before turning off the music if you start your morning with track i , or determine that you will never turn the music off. Note that if you listen to the same track several times, every time must be counted. The first line contains a single integer n ( The second line contains n integers Output n integers In the first example, here is what will happen if you start with... In the second example, if you start with track 4, you will listen to track 4, listen to track 1, listen to track 2, listen to track 3, listen to track 4 again, listen to track 1 again, and stop as 你最喜欢的音乐流媒体平台为你量身打造了一个完美平衡的播放列表。播放列表包含从1到n编号的n首歌曲,播放列表是自动循环的:每当歌曲 i 结束播放时,歌曲 i+1 开始自动播放;在歌曲 n 之后是歌曲1. 对于每个歌曲 i ,你为他定义了一个 coolness(酷?) 值 每天早上,你选择一首歌曲。播放列表从这首歌开始,以它通常的循环方式播放。在任何时候,你都记得已经播放过的歌曲的最大 coolness 值,当你听到某首coolness值严格小于 总结题意就是会给你n首歌曲的coolness值,让你输出n个数值ans,ans[i]表示从第i首歌开始听,直到听到某首歌曲coolness值小于之前听过的所有歌曲的最大coolness值的一半时就关闭音乐,这期间总共听过多少首就输出多少,如果一直停不下来就输出-1; 首先保存这n首歌的最大coolness和最小coolness值,当最小的coolness值都大于等于最大的coolness值的一半时自然歌就无限循环了,此时输出n个-1; 否则我们枚举所有n个位置,使用一个mutiset保存所有经过的点,直到枚举到值小于mutiset中最大值一半的点为止,则此时mutiset的大小就是路径长度,删除掉这个点继续下一次枚举. 暴力枚举显然极易tle,我们这里使用一个技巧,假设第i首歌为开始时是在播放第x首歌时停止的,那我们计算第i+1首歌之前自然是要在mutiset中移除第i首歌的coolness值a[i],然而第i+1首歌的停止位置可以接着从x开始判断,原因如下: 因为移除第i首歌的coolness值a[i]之后,其后路径中不是以a[i]作为最大值判断合格的点自然依旧合格,是以a[i]判断合格的点比如a[t],说明i到t之间的值都小于等于a[i],而a[t]既然大于a[i]等于/2,自然也大于等于比a[i]小的值/2,故而a[t]必然依旧合格. You are given two strings s and t, both consisting of exactly k lowercase Latin letters, s is lexicographically less than t. Let's consider list of all strings consisting of exactly k lowercase Latin letters, lexicographically not less than s and not greater than t (including s and t) in lexicographical order. For example, for k=2, s="az" and t="bf" the list will be ["az", "ba", "bb", "bc", "bd", "be", "bf"]. Your task is to print the median (the middle element) of this list. For the example above this will be "bc". It is guaranteed that there is an odd number of strings lexicographically not less than s and not greater than t. The first line of the input contains one integer k ( The second line of the input contains one string s consisting of exactly k lowercase Latin letters. The third line of the input contains one string t consisting of exactly k lowercase Latin letters. It is guaranteed that s is lexicographically less than t . It is guaranteed that there is an odd number of strings lexicographically not less than s and not greater than t. Print one string consisting exactly of k lowercase Latin letters — the median (the middle element) of list of strings of length k lexicographically not less than s and not greater than t. 你有两个字符串s和t,都是由k个小写的拉丁字母组成,s的字典序比t小。 总结题意就是已知两个字符串是s,t,分别长度k,列出一个列表包含长度为k字典序在s与t之间的所有字符串,输出中位数字符串. 其实这个字符串和我们的数字没什么差别,只是我们的数字是10进制,这个字符串是26进制,故而我们把这个字符串看作大数进行处理即可,'a'看成0,'b'看成1...'z'看成25,故而我们中位字符串的求取就模拟数字求中位数,即(a+b)/2即可. Ivan had string s consisting of small English letters. However, his friend Julia decided to make fun of him and hid the string s. Ivan preferred making a new string to finding the old one. Ivan knows some information about the string s. Namely, he remembers, that string You are to reconstruct lexicographically minimal string s such that it fits all the information Ivan remembers. Strings ti and string s consist of small English letters only. The first line contains single integer n ( The next n lines contain information about the strings. The i-th of these lines contains non-empty string It is guaranteed that the input data is not self-contradictory, and thus at least one answer always exists. Print lexicographically minimal string that fits all the information Ivan remembers. 伊万有一串由小英文字母组成的字符串。然而,他的朋友茱莉亚却拿他开玩笑,把字符串藏了起来。相比于去找旧的伊万宁愿做一根新的字符串. 总结题意就是现在已知n个字符串,以及分别在原串中出现的位置,要求重建出满足所给限制的字典序最小的字符串. 咋一看这道题的数据好些很大很大,然而由于所有字符串 我们考虑复杂度升高的核心就在重复填写同一位置字符,虽然整个答案字符串长度不超过2e6,其实某一位置的字符是什么由记忆中的一个字符串即可确定,故而我们可以预处理一个flag数组预处理记忆中字符串的所有起点,根据flag数组从左向右扫描,每个时刻仅仅确定一个剩余字符最长的当前字符串,这样的话每个位置仅仅会由一个字符串确定,效率会加速到O(n); After learning a lot about space exploration, a little girl named Ana wants to change the subject. Ana is a girl who loves palindromes (string that can be read the same backwards as forward). She has learned how to check for a given string whether it's a palindrome or not, but soon she grew tired of this problem, so she came up with a more interesting one and she needs your help to solve it: You are given an array of strings which consist of only small letters of the alphabet. Your task is to find how many palindrome pairs are there in the array. A palindrome pair is a pair of strings such that the following condition holds: at least one permutation of the concatenation of the two strings is a palindrome. In other words, if you have two strings, let's say "aab" and "abcac", and you concatenate them into "aababcac", we have to check if there exists a permutation of this new string such that it is a palindrome (in this case there exists the permutation "aabccbaa"). Two pairs are considered different if the strings are located on different indices. The pair of strings with indices (i,j) is considered the same as the pair (j,i). The first line contains a positive integer N ( Eacg of the next N lines contains a string (consisting of lowercase English letters from 'a' to 'z') — an element of the input array. The total number of characters in the input array will be less than Output one number, representing how many palindrome pairs there are in the array. The first example: The second example: 在学习了很多关于太空探索的知识后,一个名叫安娜的小女孩想要换个科目。 总结题意就是现在给你n个字符串让你输出这些字符串有多少对字符串仅仅由此两个字符串中的所有字符可以组成一个回文串. 核心在于字符串太多有1e5个,虽然输入说明所有字符串长度和在1e6以内.所以我们首先考虑什么情况下两个字符串中所有字符可能组成回文串:回文串的特点就是基于字符串中心对称,故而隐含一个属性,小于等于一种字符个数为奇数个,其余皆为偶数个时才行. 故而对于每个字符串我们可以预处理一个与之对应的特征值,特征值有26个位有效,其中第i个二进制位为1表示'a'+i字符有奇数个,否则有偶数个,这样的话我们比对两字符串的特征值是否只相差最多一个二进制位即可知晓是否可组成回文串. 然而即使如此,枚举所有字符串队依旧需要n*n,故而我们反向思考,由某个字符串出发主动寻找是否存在和我只有最多一个二进制位相差的数字,而查找存在多少个预处理之后使用二分upper_bound-lower_bound即可以logn复杂度知晓有几个. 预处理复杂度1e6,排序复杂度nlogn,查找复杂度n*27*2logn,总复杂度勉强可接受. 比赛传送门 Berland shop sells n kinds of juices. Each juice has its price Petya knows that he needs all three types of vitamins to stay healthy. What is the minimum total price of juices that Petya has to buy to obtain all three vitamins? Petya obtains some vitamin if he buys at least one juice containing it and drinks it. The first line contains a single integer n (1≤n≤1000)— the number of juices. Each of the next n lines contains an integer ci (1≤ Print -1 if there is no way to obtain all three vitamins. Otherwise print the minimum total price of juices that Petya has to buy to obtain all three vitamins. In the first example Petya buys the first, the second and the fourth juice. He spends 5+6+4=15 and obtains all three vitamins. He can also buy just the third juice and obtain three vitamins, but its cost is 16 , which isn't optimal. In the second example Petya can't obtain all three vitamins, as no juice contains vitamin "C". 伯兰商店出售n种果汁。每种果汁都有自己的价格区间.每种果汁都含有一些维生素。维生素有三种:维生素A、维生素B和维生素C。每种果汁都含有一种、两种或三种维生素。 彼佳知道他需要这三种维生素来保持健康。Petya购买三种维生素所需的果汁的最低总价是多少?如果Petya买了至少一种含维生素的果汁并饮用,他就能获得一些维生素。 总结题意就是现在有n种果汁可以买,分别有不同的价格和包含不同的维生素,要以最低的总价格买到包含三种维生素ABC的果汁. 明显的一个线性dp求最优解,只是我们需要妥善处理ABC三种维生素这种不易编码的信息,我建议基于二进制编码ABC,比如101表示含有CA,111表示含有CBA,这样的话只需要一个大小8的一维dp数组; 然后由于二进制表示的是否含有某种维生素,故而我们可以 CA+CBA=CBA 我们就是101按位或111=111,完美搞定,而转移方程: Polycarp likes numbers that are divisible by 3. He has a huge number s. Polycarp wants to cut from it the maximum number of numbers that are divisible by 3. To do this, he makes an arbitrary number of vertical cuts between pairs of adjacent digits. As a result, after m such cuts, there will be m+1 parts in total. Polycarp analyzes each of the obtained numbers and finds the number of those that are divisible by 3. For example, if the original number is s=3121, then Polycarp can cut it into three parts with two cuts: 3|1|21. As a result, he will get two numbers that are divisible by 3. Polycarp can make an arbitrary number of vertical cuts, where each cut is made between a pair of adjacent digits. The resulting numbers cannot contain extra leading zeroes (that is, the number can begin with 0 if and only if this number is exactly one character '0'). For example, 007, 01 and 00099 are not valid numbers, but 90, 0 and 10001 are valid. What is the maximum number of numbers divisible by 3 that Polycarp can obtain? The first line of the input contains a positive integer s. The number of digits of the number s is between 1 and Print the maximum number of numbers divisible by 3 that Polycarp can get by making vertical cuts in the given number s. In the first example, an example set of optimal cuts on the number is 3|1|21. In the second example, you do not need to make any cuts. The specified number 6 forms one number that is divisible by 3. In the third example, cuts must be made between each pair of digits. As a result, Polycarp gets one digit 1 and 33 digits 0. Each of the 33 digits 0 forms a number that is divisible by 3. In the fourth example, an example set of optimal cuts is 2|0|1|9|201|81. The numbers 0, 9, 201 and 81 are divisible by 3. Polycarp喜欢能被3整除的数字。 例如,如果原始的数字是s=3121,那么Polycarp可以把它分成三部分,分两部分:3|1|21。结果,他得到两个能被3整除的数。 Polycarp可以进行任意数量的垂直切割,每个切割都在相邻的两个数字之间进行。结果数字不能包含额外的前导零(也就是说,当且仅当该数字恰好是一个字符“0”时,该数字可以以0开头)。例如,007、01和00099不是有效的数字,但是90、0和10001是有效的数字。 Polycarp能获得的整除3的数字最多能有多少个? 题目倒是很清晰,是要将这2e5大小的字符串切割成多个数字,最后能被3整除的最多能有多少个,简而言之就是最优解问题. 这里考虑使用dp来统计,根据字符串位置进行状态分划使dp[i][j]表示字符串前i个字符子串切割出的最后一个数字求余3为i时能切割出的最多整除3的数字,这个dp设计的太丑了不建议学习,我继续看看能不能优化再说吧,A是A了. 比赛传送门 A and B are preparing themselves for programming contests. B loves to debug his code. But before he runs the solution and starts debugging, he has to first compile the code. Initially, the compiler displayed n compilation errors, each of them is represented as a positive integer. After some effort, B managed to fix some mistake and then another one mistake. However, despite the fact that B is sure that he corrected the two errors, he can not understand exactly what compilation errors disappeared — the compiler of the language which B uses shows errors in the new order every time! B is sure that unlike many other programming languages, compilation errors for his programming language do not depend on each other, that is, if you correct one error, the set of other error does not change. Can you help B find out exactly what two errors he corrected? The first line of the input contains integer n ( The second line contains n space-separated integers The third line contains n - 1 space-separated integers The fourth line contains n - 2 space-separated integers Print two numbers on a single line: the numbers of the compilation errors that disappeared after B made the first and the second correction, respectively. In the first test sample B first corrects the error number 8, then the error number 123. In the second test sample B first corrects the error number 1, then the error number 3. Note that if there are multiple errors with the same number, B can correct only one of them in one step. A和B正在为编程比赛做准备。 总结题意就是现在给你n个代表编译错误的数字(从样例二可知数字可重复),已知每次修改改正一个错误,且错误之间无关联,然后给你经过第一次修改之后以新顺序显示的n-1个数字,再给你经过第二次修改之后的以新顺序显示的n-2个数字,问被改正的这两个错误的数字是多少? 我们的目标就是要找到这n个数字和n-1个数字少的那一个数字,以及n-2个和n-1个相比少的那一个,然而由于数字顺序打乱以及数字可能重复造成比较困难. 由于本周是数据结构专题我们先讨论数据结构解法,这道题可使用带数目的二叉搜索树完成,先将第二行的n个数字建立二叉搜索树(红黑树最好,建议直接用map或mutiset),再将第三行的n-1个数字建立二叉搜索树,遍历输出不同的结点即可,第四行的n-2个数字于第三行相同处理,此做法3*n*logn; 也可对错误数字进行排序然后逐个比较,这样的做法也是3*n*logn; 我最建议的是通过异或运算以 n 复杂度做法完成这道题,由于修改前与修改后的所有数字只有一个数字相差,故而我们可知非被修改的数字修改前后个数加在一起一定是偶数个(比如修改前3个+修改后3个=6个),被修改的数字修改前后个数加在一起一定是奇数个,故而我们可直接将表示编译报错的数字全部异或在一起得到一个特征值,修改前后的特征值异或得到的就是被修改的数字. Reforms continue entering Berland. For example, during yesterday sitting the Berland Parliament approved as much as n laws (each law has been assigned a unique number from 1 to n). Today all these laws were put on the table of the President of Berland, G.W. Boosch, to be signed. This time mr. Boosch plans to sign 2k laws. He decided to choose exactly two non-intersecting segments of integers from 1 to n of length k and sign all laws, whose numbers fall into these segments. More formally, mr. Boosch is going to choose two integers a, b ( As mr. Boosch chooses the laws to sign, he of course considers the public opinion. Allberland Public Opinion Study Centre (APOSC) conducted opinion polls among the citizens, processed the results into a report and gave it to the president. The report contains the absurdity value for each law, in the public opinion. As mr. Boosch is a real patriot, he is keen on signing the laws with the maximum total absurdity. Help him. The first line contains two integers n and k ( Print two integers a, b — the beginning of segments that mr. Boosch should choose. That means that the president signs laws with numbers from segments [a; a + k - 1] and [b; b + k - 1]. If there are multiple solutions, print the one with the minimum number a. If there still are multiple solutions, print the one with the minimum b. In the first sample mr. Boosch signs laws with numbers from segments [1;2] and [4;5]. The total absurdity of the signed laws equals 3 + 6 + 1 + 6 = 16. In the second sample mr. Boosch signs laws with numbers from segments [1;2] and [3;4]. The total absurdity of the signed laws equals 1 + 1 + 1 + 1 = 4. 波兰改革仍在进行。例如,在昨天的会议上,波兰议会批准了多达n条法律(每一条法律都被分配了一个唯一的数字,从1到n),今天所有这些法律都被放在伯兰的总统桌上,等待签署。 这一次,波兰计划签署 2k 条法律。总统决定从1到n选择两个长度为k的互不相交的区间,并签署区间中所有的法律.更正式说,Boosch先生将选择两个整数a, b ( 在Boosch选择签署法律的同时,他当然也会考虑公众舆论。Allberland民意研究中心(APOSC)对市民进行了民意调查,并将结果整理成报告交给了总统。这份报告包含了在公众眼中每一条法律的荒谬值。由于Boosch是一个真正的爱国者,他热衷于签署荒谬至极的法律。帮助他。 总结题意就是现在有n个数字代表这n条法律的荒谬值,寻找两个不相交的长度k的区间使得荒谬值总和最大,最后要输出的就是这两个长度k的区间的开始位置. 我们需要找的是两个不相交区间,这两个区间区间和的和要尽可能大,首先长度为k的区间总共有n-k+1个,比如n为5,k为2时,长度2的区间有[0,1],[1,2],[2,3],[3,4],我们大可以先预处理出这n-k+1个区间的区间和数组seg_sum,我们要找的是两个区间且由于要求两区间不交叉故而我们无法贪心,我们可以考虑枚举第一个区间,然后第二个区间贪心的选取区间和最大的, 例如若第一个区间从i开始,第二个区间从i+k开始贪心即可保证不会交叉,故而问题变为寻找[i+k,n-k]个区间的区间和值中最大的数字 区间最大值以线段树辅助处理即可达到logn的查找效率,故而这将会是一个预处理n,枚举第一个区间n-2k,线段树查找第二个区间O(log(n-k))的总复杂度nlogn算法. 然而由于这里的区间和的值是不会变的,故而我们可以通过预处理出一个seg_max数组,seg_max[i]表示seg_sum中[i,n-k]的最大值下标,这样的话查找第二个区间即可加速到O(1),进化为总复杂度 n 算法. codeforces题目传送门 One tradition of ACM-ICPC contests is that a team gets a balloon for every solved problem. We assume that the submission time doesn't matter and teams are sorted only by the number of balloons they have. It means that one's place is equal to the number of teams with more balloons, increased by 1. For example, if there are seven teams with more balloons, you get the eight place. Ties are allowed. You should know that it's important to eat before a contest. If the number of balloons of a team is greater than the weight of this team, the team starts to float in the air together with their workstation. They eventually touch the ceiling, what is strictly forbidden by the rules. The team is then disqualified and isn't considered in the standings. A contest has just finished. There are n teams, numbered 1 through n. The i-th team has ti balloons and weight wi. It's guaranteed that ti doesn't exceed wi so nobody floats initially. Limak is a member of the first team. He doesn't like cheating and he would never steal balloons from other teams. Instead, he can give his balloons away to other teams, possibly making them float. Limak can give away zero or more balloons of his team. Obviously, he can't give away more balloons than his team initially has. What is the best place Limak can get? The first line of the standard input contains one integer n (2 ≤ n ≤ 300 000) — the number of teams. The i-th of n following lines contains two integers ti and wi (0 ≤ ti ≤ wi ≤ Print one integer denoting the best place Limak can get. In the first sample, Limak has 20 balloons initially. There are three teams with more balloons (32, 40 and 45 balloons), so Limak has the fourth place initially. One optimal strategy is: In the second sample, Limak has the second place and he can't improve it. In the third sample, Limak has just enough balloons to get rid of teams 2, 3 and 5 (the teams with 81 000 000 000, 5 000 000 000 and 46 000 000 000 balloons respectively). With zero balloons left, he will get the second place (ex-aequo with team 6 and team 7). ACM-ICPC竞赛的一个传统是一个队伍每解决一个问题就得到一个气球。我们假设提交时间无关紧要,队伍只根据他们拥有的气球数量排序。这意味着一支队伍的排名等于有更多气球的队伍的数量,每支队伍增加1。例如,如果有七支队伍有比你更多的气球,你将会是第八名。允许并列排名。 Limak是一队的一员。他不喜欢作弊,也从不偷其他队的气球。相反,他可以把他的气球送给其他队伍,可能还可以让它们漂浮起来。Limak可以送出他们队伍所拥有的零或多个气球。很明显,他送出的气球的数量不能多于他的团队最初拥有的数量。 Limak能得到的最好的排名是多少? 总结题意就是现在有n个队伍,每个队伍已知气球数和重量,第一支队伍就是Limak所在的队伍,最终排名仅仅根据气球多的在前,相同则并列,特别的如果气球数目多于队伍重量则此队伍不参与排名,Limak可将自己队伍的部分气球赠与其它队伍,输出Limak可拿到的最高排名. n个队伍仅仅通过气球数量排序,允许并列排名,就比如四支队伍分别有2 2 2 1 个气球,2 2 2三支队伍并列第一,1在第四. 在不考虑赠送气球的情况下只需要基于气球数目用sort降序排序后遍历一遍即可知道limak是第几名,可是现在允许赠送气球以使得某些队伍被取消排名资格,如果排名高于limak的队伍被取消资格那么limak的排名自然就上升了,所以我们需要考虑赠送气球给哪个队伍是最优的. 大方向上自然是赠送给排名在limak之前(气球数目比limak当前气球多)的队伍,然而赠送气球之后自己拥有的气球减少会使得排名高于limak的队伍更多,因而我们自然是要赠送最少的气球,故而我们使用一个优先队列存所有气球数比limak当前气球数多的队伍,根据"上天"需要消耗的最少气球数比较大小. 每次消灭一个"上天"消耗最少的队伍,然后更新优先队列,将新的比limak剩余气球数多的队伍压进优先队列,之后优先队列的长度+1自然就是limak队伍的排名,因为优先队列里面存的不就是所有比limak剩余气球数多的队伍吗,最优的排名一定会产生在这个不断消灭队伍的过程中. You are given a string s, consisting of lowercase English letters, and the integer m. One should choose some symbols from the given string so that any contiguous subsegment of length m has at least one selected symbol. Note that here we choose positions of symbols, not the symbols themselves. Then one uses the chosen symbols to form a new string. All symbols from the chosen position should be used, but we are allowed to rearrange them in any order. Formally, we choose a subsequence of indices Then we take any permutation p of the selected indices and form a new string Find the lexicographically smallest string, that can be obtained using this procedure. The first line of the input contains a single integer m (1 ≤ m ≤ 100 000). The second line contains the string s consisting of lowercase English letters. It is guaranteed that this string is non-empty and its length doesn't exceed 100 000. It is also guaranteed that the number m doesn't exceed the length of the string s. Print the single line containing the lexicographically smallest string, that can be obtained using the procedure described above. In the first sample, one can choose the subsequence {3} and form a string "a". In the second sample, one can choose the subsequence {1, 2, 4} (symbols on this positions are 'a', 'b' and 'a') and rearrange the chosen symbols to form a string "aab". 给定一个字符串s,由小写英文字符组成,以及整数m。 然后用选择的符号形成一个新的字符串。应该使用所选位置的所有符号,但我们可以按任何顺序重新排列它们。 更正式的说,我们选择的是某个子序列 总结题意就是从所给字符串中选取一部分字符,选出来的这部分字符要满足两个条件: 1. 所有长度为m的子段都包含至少一个被选出的字符,字符以位置区分,不同位置的a是不同的. 2. 满足条件1的前提下这些字符按字典顺序排得到的字符串是所有方案中字典序最小的. 一方面要字典序最小,一方面要满足条件1,我们明白字典序是贪心的,我们考虑用贪心解决这个问题,长度为m的子段总共 从左到右遍历所有子段,每个子段若已包含一个已选取字符则pass,不包含则贪心选取子段中最小的字符即可.子段中最小字符,简而言之就是区间最小值,用线段树解决可达logn,故而总复杂度将会是nlogn 线段树不需要考虑修改只需要区间查询功能,查询得到的应该是区间最小字符的下标. 这道题是最小字典序,要小心比如样例三 这个样例应该是选取下标2,5,6,9 的字符组成aabb即可,然而我们大可以多选一个多余的a构成aaabb使得字典序比aabb更小,故而当当前输出的字符并非被选取字符中的最大字符时,原串中的此字符有多少个就得选多少个,以此保证字典序最小. Kostya is a genial sculptor, he has an idea: to carve a marble sculpture in the shape of a sphere. Kostya has a friend Zahar who works at a career. Zahar knows about Kostya's idea and wants to present him a rectangular parallelepiped of marble from which he can carve the sphere. Zahar has n stones which are rectangular parallelepipeds. The edges sizes of the i-th of them are ai, bi and ci. He can take no more than two stones and present them to Kostya. If Zahar takes two stones, he should glue them together on one of the faces in order to get a new piece of rectangular parallelepiped of marble. Thus, it is possible to glue a pair of stones together if and only if two faces on which they are glued together match as rectangles. In such gluing it is allowed to rotate and flip the stones in any way. Help Zahar choose such a present so that Kostya can carve a sphere of the maximum possible volume and present it to Zahar. The first line contains the integer n ( n lines follow, in the i-th of which there are three integers ai, bi and ci ( In the first line print k (1 ≤ k ≤ 2) the number of stones which Zahar has chosen. In the second line print k distinct integers from 1 to n — the numbers of stones which Zahar needs to choose. Consider that stones are numbered from 1 to n in the order as they are given in the input data. You can print the stones in arbitrary order. If there are several answers print any of them. In the first example we can connect the pairs of stones: Or take only one stone: It is most profitable to take only the first stone. Kostya是个和蔼可亲的雕刻家,他有个主意:把大理石雕刻成球形。Kostya有个同行叫Zahar。Zahar知道Kostya的想法,想送给他一个长方形的平行六面体,他可以用它来雕刻球体。 Zahar有n块石头,都是长方形的平行六面体。其中第i个的边长分别为ai, bi, ci。他最多只能拿两块石头送给克斯特亚。 如果Zahar拿了两块石头,他应该把它们粘在一个面上,这样才能得到一块新的平行六面体的大理石。因此,当且仅当粘在一起的两个面矩形匹配时,才能将一对石头粘在一起。在这种粘合过程中,它可以以任何方式旋转和翻转石头。 帮助Zahar选择这样一个礼物,这样Kostya就可以雕刻一个尽可能大的球体并把它送给Zahar。 总结题意就是现在有n块平行六面体,平行六面体其实就是长方体,已知每块石头的三边长,我们要从这n个石头中选一个或两个出来,使得以选出来的石头切割出来的球体有最大半径,选了两块石头必须某个面一样,然后把两块石头粘在一起. 首先,只选一个石头的情况很简单,其实这就是个 短板效应 , 边长为a,b,c的长方体雕刻出来的最大球体直径其实就是abc中最短的边. 问题难在选两个石头的情况,这两个石头要能粘在一起(粘在一起的两面要相同),所谓的两面相同其实就是两个边长数值相同,我们难的是找到粘在一起之后新的三边长最小值最大的情况. 我们考虑枚举第一个石头,设此石头三边长为a,b,c且a<=b<=c,我们有以下三种粘法: 1.若取a,c面与另一个石块粘在一起,则由于a,c不变,b可能被填补的更高,因为a小于更加大的b,也小于c,最终ans==a,等于不粘 2.若取a,b面与另一个石块粘在一起,则由于a,b不变,c可能被填补的更高,因为a小于b,也小于更加大的b,最终ans==a,等于不粘 2.若取b,c面与另一个石块粘在一起,则由于b,c不变,a可能被填补的更高,最终ans>=a 经过分析我们知道a<=b<=c,选择最大的bc两个边长组成的面与其他石头相粘才是有效的.故而对于被枚举的每一个石头,我们在其余n-1个石头中找到同样有边长bc的石头中a最长的石头与其粘连即可,然而如果单纯遍历会tle,故而我们使用map预处理所有石头的粘连匹配情况. 比如对于石头 1 3 5我们就需要在map中压入键为(3,5)值为1的键值对,对于新的石头2 3 5,则更新键(3,5)的键值对的值为2,实际编码中map的值存的是下标idx,通过访问数组sto[idx][0]得到值. You are given an undirected graph consisting of n vertices and m edges. Your task is to find the number of connected components which are cycles. Here are some definitions of graph theory. An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex a is connected with a vertex b, a vertex b is also connected with a vertex a ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices. Two vertices u and v belong to the same connected component if and only if there is at least one path along edges connecting u and v. A connected component is a cycle if and only if its vertices can be reordered in such a way that: A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices. There are 6 connected components, 2 of them are cycles: [7,10,16] and [5,11,9,15]. The first line contains two integer numbers n and m ( The following m lines contains edges: edge i is given as a pair of vertices vi, ui (1≤vi,ui≤n, ui≠vi). There is no multiple edges in the given graph, i.e. for each pair (vi,ui) there no other pairs (vi,ui) and (ui,vi) in the list of edges. Print one integer — the number of connected components which are also cycles. In the first example only component [3,4,5] is also a cycle. The illustration above corresponds to the second example. 你得到一个由n个顶点和m条边组成的无向图。你的任务是找到循环连通块的数量。 下面是图论的一些定义。 无向图由两个集合组成:节点集(称为顶点)和边集。每条边连接一对顶点。所有的边都是双向的(也就是说,如果一个顶点a与另一个顶点b相连,那么另一个顶点b也与另一个顶点a相连)。一条边不能与自身相连,一对顶点之间最多只能有一条边。 当且仅当u和v之间有至少一条路径相连时,两个顶点u和v属于同一连通块。 一个被连通块是循环的,当且仅当它的顶点可以这样重新排序: 除了上面描述的外,循环不包含任何其他边。根据定义,任何循环都包含三个或更多的顶点。 总结题意就是给你一个n结点m边的图,让你算出图中的循环连通块的个数,循环连通块的意义如图中例子. 我们是要判断无向图中的循环连通块个数,首先什么是循环连通块,首先由于是无向图,连通块中任意两点要有路径直接或间接相连, 至于循环就是1->2->3->4->1这种单链循环. 注意题目中说明输入不会包含1,2 2,1这种相同边,也不会包含 1,1 这种自己连向自己的边. 我们经过研究可得到一个结论:在本题输入条件下,若连通块中所有结点度都为2,则是循环的. 利用这个结论,我们编码时用邻接表存图,然后做一个标志数组标志每个点是否已被访问,即可遍历所有点,对未被访问的点使用bfs去得到并标记他所在的连通块即可,判断此连通块是否全部结点度为2. Little town Nsk consists of n junctions connected by m bidirectional roads. Each road connects two distinct junctions and no two roads connect the same pair of junctions. It is possible to get from any junction to any other junction by these roads. The distance between two junctions is equal to the minimum possible number of roads on a path between them. In order to improve the transportation system, the city council asks mayor to build one new road. The problem is that the mayor has just bought a wonderful new car and he really enjoys a ride from his home, located near junction s to work located near junction t. Thus, he wants to build a new road in such a way that the distance between these two junctions won't decrease. You are assigned a task to compute the number of pairs of junctions that are not connected by the road, such that if the new road between these two junctions is built the distance between s and t won't decrease. The firt line of the input contains integers n, m, s and t (2 ≤ n ≤ 1000, 1 ≤ m ≤ 1000, 1 ≤ s, t ≤ n, s ≠ t) — the number of junctions and the number of roads in Nsk, as well as the indices of junctions where mayors home and work are located respectively. The i-th of the following m lines contains two integers Print one integer — the number of pairs of junctions not connected by a direct road, such that building a road between these two junctions won't decrease the distance between junctions s and t. Input Output Input Output Input Output 小镇Nsk由n个路口组成,由m条双向道路连接。每条道路连接两个不同的路口,没有两条道路连接同一对路口。从任何一个路口到另一个路口都可以走这条路。两个路口之间的距离等于它们之间道路上可能的最小道路数。 总结题意就是n个结点m条边的无向图,边权都是1,现在想新建一条边,问使得指定的两点s,t最短距离不变的新建方案有多少种,不存在连接相同两点的边. 我们可以分别以s和t为起点进行两次单源最短路径,然后将连接t1,t2可能造成更短路径的情况分为三段,s到t1+t1到t2+t2到t或者s到t2+t2到t1+t1到t,枚举所有的t1,t2,通过之前求好的最短路径判断是否更短. Valya and Tolya are an ideal pair, but they quarrel sometimes. Recently, Valya took offense at her boyfriend because he came to her in t-shirt with lettering that differs from lettering on her pullover. Now she doesn't want to see him and Tolya is seating at his room and crying at her photos all day long. This story could be very sad but fairy godmother (Tolya's grandmother) decided to help them and restore their relationship. She secretly took Tolya's t-shirt and Valya's pullover and wants to make the letterings on them same. In order to do this, for one unit of mana she can buy a spell that can change some letters on the clothes. Your task is calculate the minimum amount of mana that Tolya's grandmother should spend to rescue love of Tolya and Valya. More formally, letterings on Tolya's t-shirt and Valya's pullover are two strings with same length n consisting only of lowercase English letters. Using one unit of mana, grandmother can buy a spell of form (c1, c2) (where c1 and c2 are some lowercase English letters), which can arbitrary number of times transform a single letter c1 to c2 and vise-versa on both Tolya's t-shirt and Valya's pullover. You should find the minimum amount of mana that grandmother should spend to buy a set of spells that can make the letterings equal. In addition you should output the required set of spells. The first line contains a single integer n (1 ≤ n ≤ 105) — the length of the letterings. The second line contains a string with length n, consisting of lowercase English letters — the lettering on Valya's pullover. The third line contains the lettering on Tolya's t-shirt in the same format. In the first line output a single integer — the minimum amount of mana t required for rescuing love of Valya and Tolya. In the next t lines output pairs of space-separated lowercase English letters — spells that Tolya's grandmother should buy. Spells and letters in spells can be printed in any order. If there are many optimal answers, output any. In first example it's enough to buy two spells: ('a','d') and ('b','a'). Then first letters will coincide when we will replace letter 'a' with 'd'. Second letters will coincide when we will replace 'b' with 'a'. Third letters will coincide when we will at first replace 'b' with 'a' and then 'a' with 'd'. Valya和Tolya是理想的一对,但他们有时也会吵架。最近,Valya对她的男朋友很生气,因为他穿的t恤上的字和她套头衫上的字不一样。现在她不想见他,Tolya整天坐在他的房间里,对着她的照片哭泣。 总结题意就是现在有两个长度相同的字符串,我们可以使用魔法值购买咒语,一个魔法值购买的一条咒语,可以使用无限次的将一个单字符c1转换成c2,反之也可以将c2转换成c1,问将两个字符串变为一模一样最少要花多少魔法值买咒语. 这里我们的咒语是核心,因为 c1,c2 咒语能无限次并且也可双向使用,c1->c2也可c2->c1,故而若有咒语 a,b 与 b,c 我们相当于也有了咒语a,c ,咒语是具有传递性的. 既然是具有传递性的,我们就可以把26个小写字母看作并查集中的基础元素,同一集合内的字符自然可以任意互转. 我们只要遍历字符串,在两字符串中对应字符不同时,若两字符在并查集中已是同一集合,自然不必再买咒语,若不同则购买,在购买咒语c1,c2之后就可以将c1,c2所在集合合并. Heidi the Cow is aghast: cracks in the northern Wall? Zombies gathering outside, forming groups, preparing their assault? This must not happen! Quickly, she fetches her HC2 (Handbook of Crazy Constructions) and looks for the right chapter: How to build a wall: This seems easy enough. But Heidi is a Coding Cow, not a Constructing Cow. Her mind keeps coming back to point 2b. Despite the imminent danger of a zombie onslaught, she wonders just how many possible walls she could build with up to n bricks. A wall is a set of wall segments as defined in the easy version. How many different walls can be constructed such that the wall consists of at least 1 and at most n bricks? Two walls are different if there exist a column c and a row r such that one wall has a brick in this spot, and the other does not. Along with n, you will be given C, the width of the wall (as defined in the easy version). Return the number of different walls modulo The first line contains two space-separated integers n and C, 1 ≤ n ≤ 500000, 1 ≤ C ≤ 200000. Print the number of different walls that Heidi could build, modulo The number In the second sample case, the five walls are: In the third sample case, the nine walls are the five as in the second sample case and in addition the following four: 奶牛海蒂惊呆了:北边城墙上的裂缝?僵尸们聚集在外面,形成群体,准备攻击?这绝不能发生!很快,她拿起她的HC2(疯狂建筑手册),寻找对应的章节: 这似乎很简单。但海蒂是一头会编码的牛,不是一头会建筑的牛。她的思绪总是回到第二点。尽管僵尸攻击的危险迫在眉睫,她想知道她能用最多n块砖建多少堵墙。 与n一起,你将得到C,即墙的宽度(如简易版中定义的那样)。以10^{6}+3为模数,返回不同墙体的数量。 One company of IT City decided to create a group of innovative developments consisting from 5 to 7 people and hire new employees for it. After placing an advertisment the company received n resumes. Now the HR department has to evaluate each possible group composition and select one of them. Your task is to count the number of variants of group composition to evaluate. The only line of the input contains one integer n (7 ≤ n ≤ 777) — the number of potential employees that sent resumes. Output one integer — the number of different variants of group composition. 总结题意就是从n个人中选5到7个人问有几种组合. 后文用ull表示unsinged long long 答案就是 然而因为题目中的最终答案最大大约是 核心在于分子乘完之后再除m!会爆掉,我们已知组合数的分子分母必然能整除,故而我们将分子分为大小相近在ull之内的两个,分别除以部分的分子再相乘以此确保不爆掉,我的做法是取前四个作为前半段,用gcd确定分母怎么分配. There are n people sitting in a circle, numbered from 1 to n in the order in which they are seated. That is, for all i from 1 to n−1, the people with id i and i+1 are adjacent. People with id n and 1 are adjacent as well. The person with id 1 initially has a ball. He picks a positive integer k at most n, and passes the ball to his k-th neighbour in the direction of increasing ids, that person passes the ball to his k-th neighbour in the same direction, and so on until the person with the id 1 gets the ball back. When he gets it back, people do not pass the ball any more. For instance, if n=6 and k=4, the ball is passed in order [1,5,3,1]. Consider the set of all people that touched the ball. The fun value of the game is the sum of the ids of people that touched it. In the above example, the fun value would be 1+5+3=9. Find and report the set of possible fun values for all choices of positive integer k. It can be shown that under the constraints of the problem, the ball always gets back to the 1-st player after finitely many steps, and there are no more than The only line consists of a single integer n (2≤n≤ Suppose the set of all fun values is f1,f2,…,fm.Output a single line containing m space separated integers f1 through fm in increasing order. In the first sample, we've already shown that picking k=4 yields fun value 9, as does k=2. Picking k=6 results in fun value of 1. For k=3 we get fun value 5 and with k=1 or k=5 we get 21. In the second sample, the values 1, 10, 28, 64 and 136 are achieved for instance for k=16, 8, 4, 10 and 11, respectively. 有n个人坐成一个圈,按他们坐的顺序从1到n编号。也就是说,对于从1到n - 1的所有i, id为i和i+1的是相邻的。id为n和1的人也相邻。 id为1的人最初有一个球。他选择一个正整数k,最多n,然后把球传给他的第k个邻居,这个人把球传给他的第k个邻居,同样的方向,以此类推,直到id为1的人把球拿回来。当他拿回球时,人们不再传球了。 例如,如果n=6, k=4,球按[1,5,3,1]的顺序传递。 考虑所有触球的人的集合。游戏的乐趣价值是触摸它的人的id的总和。在上面的例子中,有趣的值是1+5+3=9。 发现并报告所有的选择可能有趣的设置值的正整数k。它可以表明,在问题的约束下,球总是回到1日球员有限许多步骤之后,给定的n的有趣值不会超过 总结题意就是我们的球在n个从1到n编号的人手中传递球,可以选择隔着k(n以内)个人传,传回1手上时经过的所有人的编号之和就是本次传球的有趣值,从小到大输出所有可能的有趣值. 首先既然球能传回1号手上,那么这个k就是受到了n约束的,即必须是n的因数,或者是0或6,因而我们使用优化之后的遍历方法O(根号n)的遍历n的因数然后把每个因数下得到的有趣值存入set最后输出即可. 至于因数为x时的有趣值,我们可以把经过的人的编号看作一个等差数列,这个等差数列有n/x项,首项为1,公差为x,用求和公式即可完成有趣值求取.我的代码中关于等差数列求和公式是经过化简之后的结果. You invited nguests to dinner! You plan to arrange one or more circles of chairs. Each chair is going to be either occupied by one guest, or be empty. You can make any number of circles. Your guests happen to be a little bit shy, so the i-th guest wants to have a least li free chairs to the left of his chair, and at least ri free chairs to the right. The "left" and "right" directions are chosen assuming all guests are going to be seated towards the center of the circle. Note that when a guest is the only one in his circle, the li chairs to his left and ri chairs to his right may overlap. What is smallest total number of chairs you have to use? First line contains one integer n — number of guests, (1⩽n⩽ Next n lines contain n pairs of space-separated integers li and ri (0⩽li,ri⩽ Output a single integer — the smallest number of chairs you have to use. In the second sample the only optimal answer is to use two circles: a circle with 5 chairs accomodating guests 1 and 2, and another one with 10 chairs accomodationg guests 3 and 4. In the third sample, you have only one circle with one person. The guest should have at least five free chairs to his left, and at least six free chairs to his right to the next person, which is in this case the guest herself. So, overall number of chairs should be at least 6+1=7. 你邀请了n个客人来吃饭!您计划安排一个或多个围成圈的椅子。每把椅子不是坐一个客人,就是空着。你可以做出任意数量的圆。 您的客人刚好有点害羞,所以第i位客人想要至少有 你需要使用的椅子的最小总数是多少? 总结题意就是现在有n个客人来吃饭,每个客人都要求左右分别必须有li,ri个空位,现在要安排这n个客人坐下来,可以围成任意多个圈,问需要最少几把椅子? 最劣情况是每个客人自己围成一圈,然后在这个基础上将r值与l值最相近的客人安排来合成一个圈即可达到最优的节约椅子,并且我们将比如客人a的右边安排客人b并不会影响我们对于客人a左边相邻客人的选择,左边依旧选取最优抉择. 故而我们可知这是一个贪心的匹配l,r值的问题,我们可将所有的l,r值排序后依次配对,即是最优答案. Mr. F has n positive integers, He thinks the greatest common divisor of these integers is too small. So he wants to enlarge it by removing some of the integers. But this problem is too simple for him, so he does not want to do it by himself. If you help him, he will give you some scores in reward. Your task is to calculate the minimum number of integers you need to remove so that the greatest common divisor of the remaining integers is bigger than that of all integers. The first line contains an integer n ( The second line contains nintegers, a1,a2,…,an ( Print an integer — the minimum number of integers you need to remove so that the greatest common divisor of the remaining integers is bigger than that of all integers. You should not remove all of the integers. If there is no solution, print «-1» (without quotes). In the first example, the greatest common divisor is 1 in the beginning. You can remove 1 so that the greatest common divisor is enlarged to 2. The answer is 1. In the second example, the greatest common divisor is 3 in the beginning. You can remove 6 and 9 so that the greatest common divisor is enlarged to 15. There is no solution which removes only one integer. So the answer is 2. In the third example, there is no solution to enlarge the greatest common divisor. So the answer is −1. F先生有n个正整数, 他认为这些整数的最大公因数太小了。所以他想通过移除一些整数来放大它。 但是这个问题对他来说太简单了,所以他不想自己做。如果你帮助他,他会给你一些分数作为奖励。 您的任务是计算需要删除的最小整数数量,以便剩余整数的最大公因数大于所有整数的最大公因数。 总结题意就是要删除最少的数字使得剩余数字的最大公因数比原来n个数字的最大公因数更大. 我们目的是删除最少的数字使得剩余数字的最大公因数d2比原来n个数字的最大公因数d1更大. 那么我们有一个最直观的思路就是对这n个数字除以d1的结果分别做因数分解,统计因数的出现情况,统计出现最多的那个即为我们的d2,因为他出现最多所以删除最少数字就能成为公因数. 那么因数分解我们如果采用复杂度为 题目没有要求输出删除后的最大公因数,仅要求输出最少删除多少个,故而我们可以从这里下手优化. 首先我们需要了解唯一分解定理:大于1的合数都可以分解为有限个质数的乘积. 故而我们假设若d2是一个合数,出现了x次,是出现最多的,那么他也可以分解为多个质数的乘积,而这些质数他们在n个数字中一定也刚好出现了x次,不多不少,不少是因为这些质数作为d2的因数,光d2就出现了x次,而不多是因为如果多于x次则和d2的出现最多不就自相矛盾了吗. 故而我们仅仅需要进行质因数分解,出现最多的质因数必然是d2的因数,他的出现次数就是d2的出现次数,虽然我们并不知道这个d2到底是多少.而质因数分解通过欧拉筛法预处理质数,考虑到因数是成对的,我们只用处理 这里要额外提到若试除了 Today Pari and Arya are playing a game called Remainders. Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value . There are n ancient numbers Note, that x mod y means the remainder of x after dividing it by y. The first line of the input contains two integers n and k ( The second line contains n integers Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise. In the first sample, Arya can understand x mod 5 because 5 is one of the ancient numbers. In the second sample, Arya can't be sure what x mod 7 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7. 今天,Pari 和Arya 在玩一种叫做“余数”的游戏。 Pari 选择了两个正整数x和k,并告诉Arya k是多少,但没有说x。艾莉亚必须找到x mod k的值。有n个给定好的数 注意,x mod y是指x除以y后的余数。 总结题意就是Pari选择了正整数x和k,你只知道k是多少,要求你回答x mod k的结果是否是唯一的,光是这样肯定答不出来,你还能询问Pari这个x mod 其余n个整数的结果,以此帮助你回答x mod k. 由于k已知,故而回答x mod k是否唯一就是要确定x是否唯一,而已知条件可以总结为如下方程组,其中 我们就是要求解这个方程组中的x,而这其实就是中国剩余定理(又名孙子定理)在模数不确定是否两两互质的情况下的扩展,作为解题博客不对剩余定理及其解法做分析. 在扩展中国剩余定理中模数不确定是否两两互质,这种情况就采用两两合并的思想,假设要合并如下两个方程 那么得到 再利用扩展欧几里得算法解出 得到 lcm表示最小公倍数,这样一直合并下去,最终可以求得同余方程组的解 然而这里我们并不知道 那么 AC代码:
1.dp加对角线扫描
#include 2.dp加bfs
#include D - Thematic Contests
![]() , and some problems' topics may coincide.
, and some problems' topics may coincide.
Input
![]() ) — the number of problems Polycarp has prepared.
) — the number of problems Polycarp has prepared.![]() where ai is the topic of the i-th problem.
where ai is the topic of the i-th problem.Output
Examples
Input
18
2 1 2 10 2 10 10 2 2 1 10 10 10 10 1 1 10 10
Output
14
Input
10
6 6 6 3 6 1000000000 3 3 6 6
Output
9
Input
3
1337 1337 1337
Output
3
Note
题意:
![]() ,有些问题的主题可能是一致的。
,有些问题的主题可能是一致的。
思路:
AC思路:
#include E - Balanced Playlist
![]() . The higher
. The higher ![]() is, the cooler track i is.
is, the cooler track i is.![]() (no rounding) starts playing, you turn off the music immediately to keep yourself in a good mood.
(no rounding) starts playing, you turn off the music immediately to keep yourself in a good mood.Input
![]() ), denoting the number of tracks in the playlist.
), denoting the number of tracks in the playlist.![]() (
(![]() ), denoting coolnesses of the tracks.
), denoting coolnesses of the tracks.Output
![]() where
where ![]() is either the number of tracks you will listen to if you start listening from track i or −1 if you will be listening to music indefinitely.
is either the number of tracks you will listen to if you start listening from track i or −1 if you will be listening to music indefinitely.Examples
Input
4
11 5 2 7
Output
1 1 3 2
Input
4
3 2 5 3
Output
5 4 3 6
Input
3
4 3 6
Output
-1 -1 -1
Note
![]() .
.![]() .
.![]() .
.![]() .
.![]() Note that both track 1 and track 4 are counted twice towards the result.
Note that both track 1 and track 4 are counted twice towards the result.题意:
![]() 。
。![]() 值越高,歌曲 i 越酷。
值越高,歌曲 i 越酷。![]() (不要四舍五入)的歌曲开始播放时,为了让自己保持一个好心情,你立即关掉音乐播放器.
(不要四舍五入)的歌曲开始播放时,为了让自己保持一个好心情,你立即关掉音乐播放器.
对于每个歌曲 i ,如果你早上第一首听的是歌曲 i ,找出在你关掉音乐之前会听多少首歌曲,或者决定你永远都不会关掉歌曲。注意,如果你听到同一首歌曲多次,每次都要被数进来。思路:
AC代码:
#include F - Median String
Input
![]() ) — the length of strings.
) — the length of strings.Output
Examples
Input
2
az
bf
Output
bc
Input
5
afogk
asdji
Output
alvuw
Input
6
nijfvj
tvqhwp
Output
qoztvz
题意:
让我们按字典序来列出一个列表,包含所有由k个小写拉丁字母组成字典序不小于s不大于t(包括s和t)的字符串。例如,对于k=2, s="az"和t=“bf”列表将会是(“az”,“ba”,“bb”,“bc”,“bd”,“be”,“bf”)。
您的任务是打印这个列表的中位数(中间元素)。对于上面的例子,这将是“bc”。
输入保证有奇数个字符串的字典序不小于s不大于t。思路:
AC代码:
#include G - String Reconstruction
![]() occurs in string s at least
occurs in string s at least ![]() times or more, he also remembers exactly
times or more, he also remembers exactly ![]() positions where the string
positions where the string ![]() occurs in string s: these positions are
occurs in string s: these positions are ![]() He remembers n such strings ti.
He remembers n such strings ti.Input
![]() ) — the number of strings Ivan remembers.
) — the number of strings Ivan remembers.![]() , then positive integer
, then positive integer ![]() , which equal to the number of times the string
, which equal to the number of times the string ![]() occurs in string s, and then
occurs in string s, and then ![]() distinct positive integers
distinct positive integers ![]() in increasing order — positions, in which occurrences of the string ti in the string s start. It is guaranteed that the sum of lengths of strings ti doesn't exceed
in increasing order — positions, in which occurrences of the string ti in the string s start. It is guaranteed that the sum of lengths of strings ti doesn't exceed ![]() ,
, ![]() ,
, ![]() , and the sum of all ki doesn't exceed
, and the sum of all ki doesn't exceed ![]() . The strings
. The strings ![]() can coincide.
can coincide.Output
Examples
Input
3
a 4 1 3 5 7
ab 2 1 5
ca 1 4
Output
abacaba
Input
1
a 1 3
Output
aaa
Input
3
ab 1 1
aba 1 3
ab 2 3 5
Output
ababab题意:
Ivan知道一些关于字符串s的信息。也就是说,他记得,字符串 ![]() 在字符串s中出现至少
在字符串s中出现至少 ![]() 次或更多,他还记得字符串
次或更多,他还记得字符串 ![]() 在字符串s中 出现的确切位置:这些位置是
在字符串s中 出现的确切位置:这些位置是 ![]() 他能记住的由n条这样的字符串。
他能记住的由n条这样的字符串。
你要按照字典顺序重建最小的字符串,使它符合Ivan所记得的所有信息。字符串 ![]() 和字符串s由很小的英文字母组成
和字符串s由很小的英文字母组成思路:
![]() 的和不超过1e6,所有
的和不超过1e6,所有 ![]() 的和不超过1e6故而这道题依旧可做.
的和不超过1e6故而这道题依旧可做.AC代码:
#include H - Palindrome Pairs
Input
![]() ), representing the length of the input array.
), representing the length of the input array.![]() .
.Output
Examples
Input
3
aa
bb
cd
Output
1
Input
6
aab
abcac
dffe
ed
aa
aade
Output
6
Note
题意:
安娜是一个喜欢回文的女孩。她已经学会了如何检查给定的字符串是否为回文,但很快她就厌倦了这个问题,所以她想出了一个更有趣的问题,她需要你的帮助来解决它:
你有一个字符串数组,只由字母表中小写字母组成。你的任务是找出数组中有多少个回文对。回文对是这样的一对字符串:两个字符串连接的至少一个排列是回文。换句话说,如果你有两个字符串,比如“aab”和“abcac”,你把它们连接到“aababcac”,我们必须检查这新字符串是否存在一个回文的排列(在这种情况下,存在“aabccbaa”的排列)。
如果字符串位于不同的索引上,则认为两对是不同的。索引为(i,j)和(j,i)的字符串对被认为是相同的一对.思路:
AC代码:
#include LSNU寒假第二场(动态规划)
A - Vitamins
![]() . Each juice includes some set of vitamins in it. There are three types of vitamins: vitamin "A", vitamin "B" and vitamin "C". Each juice can contain one, two or all three types of vitamins in it.
. Each juice includes some set of vitamins in it. There are three types of vitamins: vitamin "A", vitamin "B" and vitamin "C". Each juice can contain one, two or all three types of vitamins in it.Input
![]() ≤100000) and a string si — the price of the i-th juice and the vitamins it contains. String si contains from 1 to 3 characters, and the only possible characters are "A", "B" and "C". It is guaranteed that each letter appears no more than once in each string si. The order of letters in strings
≤100000) and a string si — the price of the i-th juice and the vitamins it contains. String si contains from 1 to 3 characters, and the only possible characters are "A", "B" and "C". It is guaranteed that each letter appears no more than once in each string si. The order of letters in strings ![]() is arbitrary.
is arbitrary.Output
Examples
Input
4
5 C
6 B
16 BAC
4 A
Output
15
Input
2
10 AB
15 BA
Output
-1
Input
5
10 A
9 BC
11 CA
4 A
5 B
Output
13
Input
6
100 A
355 BCA
150 BC
160 AC
180 B
190 CA
Output
250
Input
2
5 BA
11 CB
Output
16
Note
题意:
思路:
![]()
AC代码:
#include B - Polycarp and Div 3
Input
![]() , inclusive. The first (leftmost) digit is not equal to 0.
, inclusive. The first (leftmost) digit is not equal to 0.Output
Examples
Input
3121
Output
2
Input
6
Output
1
Input
1000000000000000000000000000000000
Output
33
Input
201920181
Output
4
Note
题意:
他有一个很大的数s,Polycarp想从中剪出尽可能多的能被3整除的数。为此,他在相邻数字对之间进行任意数量的垂直切割。因此,经过m个这样的切割后,总共会有m+1个零件。Polycarp分析每个得到的数并找出数字之中能被3整除的数。思路:
AC代码:
#include
LSNU寒假第三场(数据结构)
A - A and B and Compilation Errors
Input
![]() ) — the initial number of compilation errors.
) — the initial number of compilation errors.![]() (
(![]() ) — the errors the compiler displayed for the first time.
) — the errors the compiler displayed for the first time.![]() — the errors displayed at the second compilation. It is guaranteed that the sequence in the third line contains all numbers of the second string except for exactly one.
— the errors displayed at the second compilation. It is guaranteed that the sequence in the third line contains all numbers of the second string except for exactly one.![]() — the errors displayed at the third compilation. It is guaranteed that the sequence in the fourth line contains all numbers of the third line except for exactly one.
— the errors displayed at the third compilation. It is guaranteed that the sequence in the fourth line contains all numbers of the third line except for exactly one.Output
Examples
Input
5
1 5 8 123 7
123 7 5 1
5 1 7
Output
8
123
Input
6
1 4 3 3 5 7
3 7 5 4 3
4 3 7 5
Output
1
3
Note
题意:
B喜欢调试他的代码。但是在运行解决方案并开始调试之前,必须先编译代码。
最初,编译器显示n个编译错误,每个错误都表示为正整数。经过一番努力,B终于改正了其中一个和另一个的错误。
然而,尽管B确信他改正了这两个错误,但他不能确切地理解是什么编译错误消失了——B使用的语言的编译器每次都以新顺序显示错误!B确信,与许多其他编程语言不同,他的编程语言的编译错误并不相互依赖,也就是说,如果你纠正了一个错误,其他错误的集合也不会改变。
你能帮B找出他到底改正了哪两个错误吗?思路:
AC代码:
1.异或 O(n)
#include 2.map O(3*n*logn)
#include B - Maximum Absurdity
![]() ) and sign all laws with numbers lying in the segments [a; a + k - 1] and [b; b + k - 1] (borders are included).
) and sign all laws with numbers lying in the segments [a; a + k - 1] and [b; b + k - 1] (borders are included).Input
![]() , 0 < 2k ≤ n) — the number of laws accepted by the parliament and the length of one segment in the law list, correspondingly. The next line contains n integers
, 0 < 2k ≤ n) — the number of laws accepted by the parliament and the length of one segment in the law list, correspondingly. The next line contains n integers ![]() — the absurdity of each law (
— the absurdity of each law (![]() ).
).Output
Examples
Input
5 2
3 6 1 1 6
Output
1 4
Input
6 2
1 1 1 1 1 1
Output
1 3
Note
题意:
![]() ),并签署所有[a;a + k - 1]和[b;b + k - 1](包括边框)中的所有法律。
),并签署所有[a;a + k - 1]和[b;b + k - 1](包括边框)中的所有法律。思路:
AC代码:
1.预处理 O(n)
#include 2.线段树 O(nlogn)
#include C - Contest Balloons
Input
![]() ) — respectively the number of balloons and the weight of the i-th team. Limak is a member of the first team.
) — respectively the number of balloons and the weight of the i-th team. Limak is a member of the first team.Output
Examples
Input
8
20 1000
32 37
40 1000
45 50
16 16
16 16
14 1000
2 1000
Output
3
Input
7
4 4
4 4
4 4
4 4
4 4
4 4
5 5
Output
2
Input
7
14000000003 1000000000000000000
81000000000 88000000000
5000000000 7000000000
15000000000 39000000000
46000000000 51000000000
0 1000000000
0 0
Output
2
Note
题意:
你一定知道比赛前吃东西是很重要的。如果一个队伍的气球数量大于这个队伍的总重量,这个队伍将会和他们的比赛桌一起漂浮在空中。他们将触及天花板,这是规则严格禁止的。随后该队将被取消资格,也不会被考虑进入积分榜。
比赛刚刚结束。有n个队,编号从1到n。第i个队有ti气球和wi重量。它保证ti不超过wi,所以没有人一开始是浮动的。思路:
AC代码:
#include D - Dense Subsequence
![]() . The selected sequence must meet the following condition: for every j such that 1 ≤ j ≤ |s| - m + 1, there must be at least one selected index that belongs to the segment [j, j + m - 1], i.e. there should exist a k from 1 to t, such that
. The selected sequence must meet the following condition: for every j such that 1 ≤ j ≤ |s| - m + 1, there must be at least one selected index that belongs to the segment [j, j + m - 1], i.e. there should exist a k from 1 to t, such that![]() .
.![]() .
.Input
Output
Examples
Input
3
cbabc
Output
a
Input
2
abcab
Output
aab
Input
3
bcabcbaccba
Output
aaabb
Note
题意:
我们应该从给定的字符串中选择一些字符,以便任何长度为m的连续子段至少有一个选定的符号。注意,这里我们选择的是符号的位置,而不是符号本身。![]() 。选择的顺序必须符合以下条件:对于每个 1 ≤ j ≤ |s| - m + 1 的 j ,在( j, j + m - 1)必须有至少一个被选中的下标,即从1到t,应该存在一个k使得
。选择的顺序必须符合以下条件:对于每个 1 ≤ j ≤ |s| - m + 1 的 j ,在( j, j + m - 1)必须有至少一个被选中的下标,即从1到t,应该存在一个k使得![]() 。
。
然后我们取所选索引的任意排列p,形成一个新的字符串 ![]() 。
。
查找通过以上步骤可以获得的按字典顺序排列的最小字符串。思路:
![]() 个.
个. 3
bcabcbaccbaAC代码:
#include E - Kostya the Sculptor
Input
![]() ).
).![]() ) — the lengths of edges of the i-th stone. Note, that two stones may have exactly the same sizes, but they still will be considered two different stones.
) — the lengths of edges of the i-th stone. Note, that two stones may have exactly the same sizes, but they still will be considered two different stones.Output
Examples
Input
6
5 5 5
3 2 4
1 4 1
2 1 3
3 2 4
3 3 4
Output
1
1
Input
7
10 7 8
5 10 3
4 2 6
5 5 5
10 2 8
4 2 1
7 7 7
Output
2
1 5
Note
题意:
思路:
AC代码:
#include LSNU寒假第四场(图论+搜索)
A - Cyclic Components
Input
![]() ,
, ![]() ) — number of vertices and edges.
) — number of vertices and edges.Output
Examples
Input
5 4
1 2
3 4
5 4
3 5
Output
1
Input
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
Output
2
Note
题意:
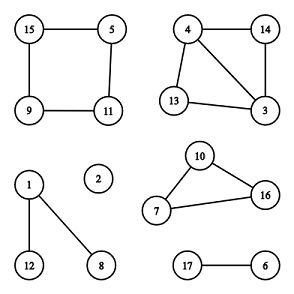
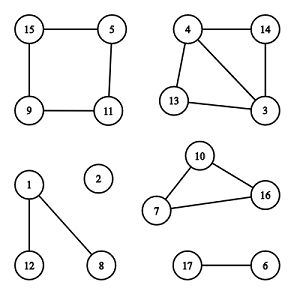
比如上图,图中共有6个连通分量,其中2个为循环:[7,10,16]和[5,11,9,15]。思路:
AC代码:
#include B - Fight Against Traffic
Input
![]() and
and ![]() (1 ≤
(1 ≤ ![]() ,
, ![]() ≤ n,
≤ n, ![]() ≠
≠ ![]() ), meaning that this road connects junctions ui and vi directly. It is guaranteed that there is a path between any two junctions and no two roads connect the same pair of junctions.
), meaning that this road connects junctions ui and vi directly. It is guaranteed that there is a path between any two junctions and no two roads connect the same pair of junctions.Output
Examples
5 4 1 5
1 2
2 3
3 4
4 5
0
5 4 3 5
1 2
2 3
3 4
4 5
5
5 6 1 5
1 2
1 3
1 4
4 5
3 5
2 5
3题意:
为了改善交通系统,市议会要求市长修一条新路。问题是,市长刚买了一个很棒的新汽车,他很喜欢从他在结点s旁边的家开车到结点t附近工作。因此,他想要建立一个新的道路,但这两个结点之间的距离不会减少。
你被分配了一项任务来计算没有被道路连接的路口对的数量,这样如果在这两个路口之间建立了新的道路,s和t之间的距离就不会减少。思路:
AC代码:
#include C - Love Rescue
Input
Output
Examples
Input
3
abb
dad
Output
2
a d
b aInput
8
drpepper
cocacola
Output
7
l e
e d
d c
c p
p o
o r
r a
Note
题意:
这个故事可能是非常悲伤的,但仙女教母(Tolya的祖母)决定帮助他们,恢复他们的关系。她偷偷拿走了Tolya的t恤和Valya的套衫,想把上面的字母拼在一起。为了做到这一点,她可以用一个单位的魔法买一个可以改变衣服上一些字母的咒语。你的任务是计算出Tolya的祖母应该花费的最小法力值来拯救Tolya和Valya的爱。
更正式的说法是,Tolya的t恤和Valya的套衫上的字母是两根长度相同的字符串,只有小写的英文字母。使用一个单位的魔法,祖母可以买一个形式的咒语(c1, c2)(其中c1和c2是一些小写的英文字母),它可以任意次数地将一个字母c1转换成c2,反之亦然。你应该找到祖母应该花的最小的魔法值来买一套咒语,使字母相等。此外,你应该输出所需的法术。思路:
AC代码:
#include LSNU寒假第五场(数论)
A - The Wall (medium)
![]() .
.Input
Output
![]() .
.Examples
Input
5 1
Output
5
Input
2 2
Output
5
Input
3 2
Output
9
Input
11 5
Output
4367
Input
37 63
Output
230574
Note
![]() is prime.
is prime. B B
B., .B, BB, B., and .B
B B
B B B B
B., .B, BB, and BB题意:
如何建造一堵墙:
简单的说一堵墙就是一段段墙的集合,有多少种不同的墙是由至少1个和最多n个砖块组成的?如果存在c列和r列一面墙在这里有一块砖,而另一面墙没有砖,那么两面墙是不同的。思路:
AC代码:
B - Selection of Personnel
Input
Output
Examples
Input
7
Output
29题意:
IT城的一家公司决定创建一个由5到7人组成的创新开发团队,并为其雇佣新员工。这家公司登广告后,收到了n份简历。现在,人力资源部门必须评估每一个可能的团队组成,并从中选择一个。你的任务是计算要评估的组组成变量的数量。思路:
![]() ,核心难点在于n最大777,
,核心难点在于n最大777,![]() 会爆掉ull,故而建议用大数处理(java bignumber欢迎你)计算.
会爆掉ull,故而建议用大数处理(java bignumber欢迎你)计算.![]() 这个答案是在 ull 以内的,故而推断这道题可以卡量级.
这个答案是在 ull 以内的,故而推断这道题可以卡量级.1.卡量级
#include 2.java 大数
C - New Year and the Sphere Transmission
![]() possible fun values for given n.
possible fun values for given n.Input
![]() ) — the number of people playing with the ball.
) — the number of people playing with the ball.Output
Examples
Input
6
Output
1 5 9 21
Input
16
Output
1 10 28 64 136
Note
题意:
![]() 。
。思路:
AC代码:
#include D - Social Circles
Input
![]() ).
).![]() ).
).Output
Examples
Input
3
1 1
1 1
1 1
Output
6
Input
4
1 2
2 1
3 5
5 3
Output
15
Input
1
5 6
Output
7
Note
题意:
![]() 把空椅子在他椅子的左边,至少有
把空椅子在他椅子的左边,至少有 ![]() 把空椅子在右边。选择“左”和“右”的方向时假设所有的客人都坐来面向圆心。注意当客人是他圈子里唯一的人时,他左边的li椅和他右边的ri椅可能重叠。
把空椅子在右边。选择“左”和“右”的方向时假设所有的客人都坐来面向圆心。注意当客人是他圈子里唯一的人时,他左边的li椅和他右边的ri椅可能重叠。思路:
AC代码:
#include E - Enlarge GCD
![]() .
.Input
![]() ) — the number of integers Mr. F has.
) — the number of integers Mr. F has.![]() ).
).Output
Examples
Input
3
1 2 4
Output
1Input
4
6 9 15 30
Output
2Input
3
1 1 1
Output
-1Note
题意:
![]() 。
。思路:
![]() 的试除法,由于数字最大15e6,单个数字因数分解复杂度4e3,数字总共3e5个,总复杂度会在12e8附近,预测会TLE.这里我们可以考虑使用
的试除法,由于数字最大15e6,单个数字因数分解复杂度4e3,数字总共3e5个,总复杂度会在12e8附近,预测会TLE.这里我们可以考虑使用![]() 的pollar_rho算法进行效率优化,或者使用像我以下的做法.
的pollar_rho算法进行效率优化,或者使用像我以下的做法.![]() 以内的质因数出现情况即可,
以内的质因数出现情况即可,![]() 以内因数大概1e3个,故而最低效率会在3e5*1e3=3e8左右,加上一些优化已经可以接受.
以内因数大概1e3个,故而最低效率会在3e5*1e3=3e8左右,加上一些优化已经可以接受.![]() 以内的质因数之后结果仍然不为1说明剩下的这个数字本身是一个[
以内的质因数之后结果仍然不为1说明剩下的这个数字本身是一个[![]() ,15e6]以内的质数,这个要额外处理.15e6这个数据大小是可以开数组的,故而我们可以通过一个15e6大小的数组来存质因数的出现情况.
,15e6]以内的质数,这个要额外处理.15e6这个数据大小是可以开数组的,故而我们可以通过一个15e6大小的数组来存质因数的出现情况.AC代码:
#include G - Remainders Game
![]() and Pari has to tell Arya x mod
and Pari has to tell Arya x mod ![]() if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value x mod k for any positive integer x?
if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value x mod k for any positive integer x?Input
![]() ) — the number of ancient integers and value k that is chosen by Pari.
) — the number of ancient integers and value k that is chosen by Pari.![]() (
(![]() ).
).Output
Examples
Input
4 5
2 3 5 12
Output
Yes
Input
2 7
2 3
Output
NoNote
题意:
![]() ,如果艾莉亚想要的话,帕里必须告诉艾莉亚x mod
,如果艾莉亚想要的话,帕里必须告诉艾莉亚x mod ![]() 的结果。给定k和那n个数,告诉我们艾莉亚是否有一个独立于x值的制胜策略。正式地说,艾莉亚能推出对任意正整数x的x mod k值吗?
的结果。给定k和那n个数,告诉我们艾莉亚是否有一个独立于x值的制胜策略。正式地说,艾莉亚能推出对任意正整数x的x mod k值吗?思路:
![]() ,分别是Pari关于每一个x mod
,分别是Pari关于每一个x mod ![]() 将会给出的答案.
将会给出的答案.![]()
![]()
![]() 的最小正整数解,再带入
的最小正整数解,再带入![]() 得x的最小正整数解
得x的最小正整数解![]()
![]()
![]() 后合并两个方程的结果为
后合并两个方程的结果为![]()
![]() 。
。![]() ,我们只是要判断这个同余数方程组的解求余k是否答案唯一确定.
,我们只是要判断这个同余数方程组的解求余k是否答案唯一确定.![]() 答案唯一说明什么呢,说明
答案唯一说明什么呢,说明![]() 等于0,故而这道题就是要判断n个模数的最小公倍数是否整除k
等于0,故而这道题就是要判断n个模数的最小公倍数是否整除kAC代码:
#include