超立方体及其可视化(Processing)
文章目录
- 1 超立方体
- 2 Processing实现可视化
- 3 拓展知识(图论)
- 4 参考资料
1 超立方体
百度百科对超立方体的描述:超立方体是数学中立方体的四维类似物,所谓的点动成线,线动成面,面动成体。在四维空间(非三维-时间概念)中,立方体的移动形成四维的超立方体,由无数个立方体所组成的,具有四维的观念。
在几何学中,超立方体是立方体的四维类比,有8个立方体胞。四维超正方体之于立方体,就如立方体之于正方形。它是四维欧式空间中6个四维凸正多胞体之一。
那么它的概念图呢,就长成下面这样。
下面解释一下这个概念图是怎么来的。拿我们三维空间举例子,我们就生活在三维空间,我们眼中看到的景象全部都是物体在我们视网膜上的投影,也就是说我们眼中的其实是三维空间的物体到二维平面上的投影。借助这个思路,虽然我们没办法想象超立方体是什么样的,但是我们可以借助投影,将四维下的超立方体投影到三维空间下,我们不就能看见了么。所以上面这个概念图,它就是超立方体在三维空间下的投影。
2 Processing实现可视化
知道了它是投影来的,我们就可以用一些工具,来模拟一下这个投影,这里我用的是Processing,利用旋转矩阵旋转超立方体,运行出来就是下面这个样子。
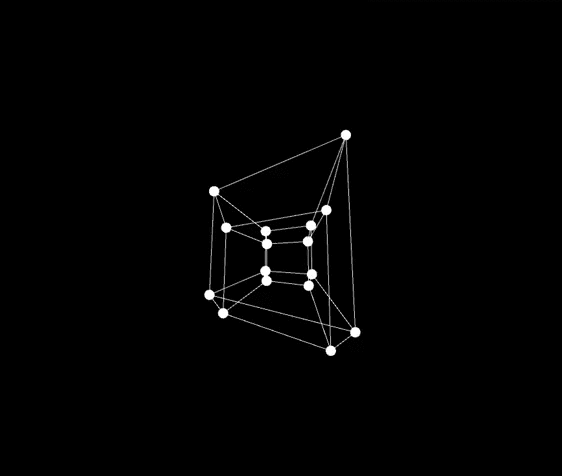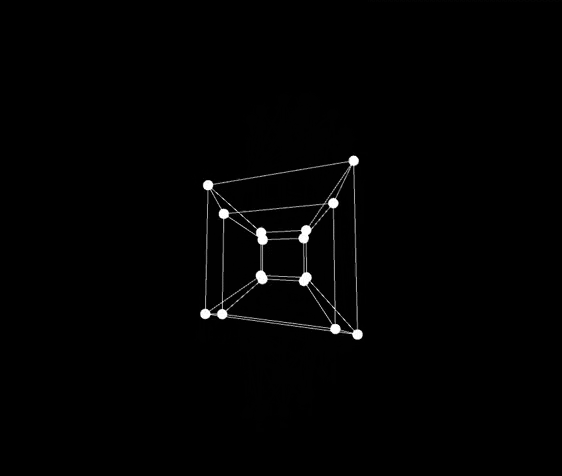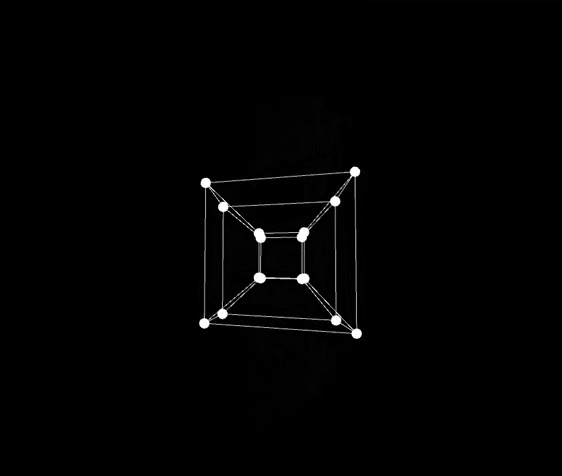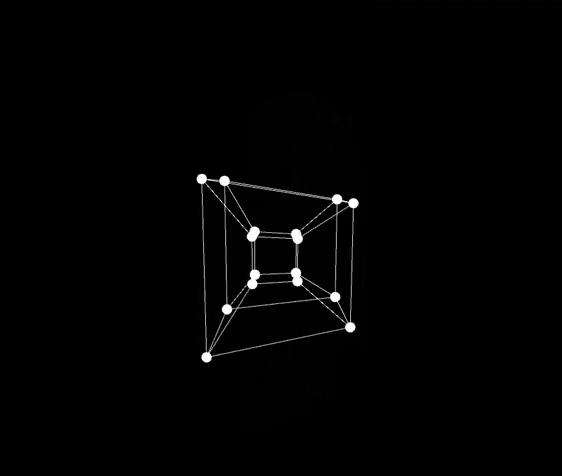
下面是代码,有兴趣的朋友可以自己下载一个Processing,运行一下玩一玩。
theta = 0
points = []
def setup():
size(1000, 800, P3D)
global points
# 四维空间下超立方体16个顶点的坐标
points =[[-100, -100, -100, 100],
[100, -100, -100, 100],
[100, 100, -100, 100],
[-100, 100, -100, 100],
[-100, -100, 100, 100],
[100, -100, 100, 100],
[100, 100, 100, 100],
[-100, 100, 100, 100],
[-100, -100, -100, -100],
[100, -100, -100, -100],
[100, 100, -100, -100],
[-100, 100, -100, -100],
[-100, -100, 100, -100],
[100, -100, 100, -100],
[100, 100, 100, -100],
[-100, 100, 100, -100]]
def draw():
global theta, points
background(0)
translate(width/2, height/2)
rotateY(-PI/2)
projected3d = []
for v in points:
stroke(255)
strokeWeight(16)
noFill()
# 一堆旋转矩阵
rotationXY = [[cos(theta), -sin(theta), 0, 0],
[sin(theta), cos(theta), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
rotationXZ = [[cos(theta), 0, -sin(theta), 0],
[0, 1, 0, 0],
[sin(theta), 0, cos(theta), 0],
[0, 0, 0, 1]]
rotationXW = [[cos(theta), 0, 0, -sin(theta)],
[0, 1, 0, 0],
[0, 0, 1, 0],
[sin(theta), 0, 0, cos(theta)]]
rotationZW = [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, cos(theta), -sin(theta)],
[0, 0, sin(theta), cos(theta)]]
rotationYW = [[1, 0, 0, 0],
[0, cos(theta), -sin(theta), 0],
[0, 0, 1, 0],
[0, sin(theta), 0, cos(theta)]]
rotationYZ = [[1, 0, 0, 0],
[0, cos(theta), -sin(theta), 0],
[0, sin(theta), cos(theta), 0],
[0, 0, 0, 1]]
v = matmul(rotationXY, v)
v = matmul(rotationZW, v)
# 投影
w = 100 / (200 - v[3])
projection = [[w, 0, 0, 0],
[0, w, 0, 0],
[0, 0, w, 0]]
v = matmul(projection, v)
projected3d.append(v)
point(v[0], v[1], v[2])
for i in range(4):
connect(0, i, (i+1) % 4, projected3d)
connect(0, i+4, ((i+1) % 4)+4, projected3d)
connect(0, i, i+4, projected3d)
for i in range(4):
connect(8, i, (i+1) % 4, projected3d)
connect(8, i+4, ((i+1) % 4)+4, projected3d)
connect(8, i, i+4, projected3d)
for i in range(8):
connect(0, i, i+8, projected3d)
theta += 0.03
# 连接点
def connect(offset, i, j, points):
i, j = i + offset, j + offset
stroke(255)
strokeWeight(1)
line(points[i][0], points[i][1], points[i][2],
points[j][0], points[j][1], points[j][2])
# 矩阵乘法
def matmul(a, b):
rowsA, colsA = len(a), len(a[0])
res = []
for i in range(rowsA):
n = 0
for j in range(colsA):
n += a[i][j]*b[j]
res.append(n)
return res
3 拓展知识(图论)
定义: k − k- k−维立方体或超方体 Q k Q_k Qk是一个简单图,其顶点是分量取自 { 0 , 1 } \{0,1\} {0,1}的所有 k − k- k−元组,边是恰在一个位置上取不同值的 k k k元组对。 Q k Q_k Qk的一个 j − j- j−维子立方体是同构与 Q j Q_j Qj的 Q k Q_k Qk的子图。
我们知道的正方体就是 Q 3 Q_3 Q3,上面讲的超立方体就是 Q 4 Q_4 Q4
超方体是一种很自然的计算机结构。如果处理器对应于 Q k Q_k Qk中的邻接节点,则它们之间可以直接通信。用来命名顶点的 k k k元组可以视作处理器的地址
超方体的结构: Q k Q_k Qk中顶点的奇偶性是由该顶点的名字中包含的1的个数的奇偶性而决定的。 Q k Q_k Qk中每条边有一个偶端点和一个奇端点。因此,偶顶点构成一个独立集,奇顶点也构成一个独立集,进而 Q k Q_k Qk是一个二部图。
k k k元组的每个分量可以取两个值,所以 n ( Q k ) = 2 k n(Q_k)=2^k n(Qk)=2k。对于一个顶点,确定其名字中的一个位置并将该位置的值修改成另一个值,就可以得到它的一个相邻顶点。于是, Q k Q_k Qk是 k − k- k−正则的。由于含有 n n n个顶点的 k − k- k−正则图有 n k / 2 nk/2 nk/2条边,所以 e ( Q k ) = k 2 k − 1 e(Q_k)=k2^{k-1} e(Qk)=k2k−1
4 参考资料
- 百度百科超立方体
- 代码实现参考的bilibili上的一个视频
- 《图论导引》P26,定义1.3.7
