背包问题详解

导言

部分背包问题

0 1 背包问题

完全背包问题

多重背包问题

背包的分类

一级包，二级包和三级包，显然其中三级包的容量是最大的，吃鸡必备装备啊！

但是我们需要研究的是这样的问题：

各种背包

背包问题大概分下面这几种

• 部分背包问题
• 0 1 背包问题
• 完全背包问题
• 多重背包问题

问题

为什么要学习背包问题呢？

• 背包问题已经是一个很经典而且讨论很广泛的算法问题了。
• 背包问题的解决方法背后其实隐藏了两种我们比较常见的算
  法解决思路，动态规划和贪心算法。

---

部分背包

定义：

部分背包问题：

给出 n 个物体，第 i 个物体重量为 wi, 价值为 vi。在总重量
不超过 W 的情况下让总价值尽量高，每一个物体都可以只取走
一部分，价值和重量按比例计算。

分析

因为物体既有重量又有价值，所以不能简单的先拿轻的 (轻
的可能价值也小)，也能先拿价值大的 (它可能特别重)，而因该
综合考虑两个因素。一种直观的贪心策略就是：优先拿“价值除
以重量”最大的，直到重量和正好为 W

那么你作为一个非常优秀的 ACMer，肯定应该知道按照什
么顺序拿物品的把。没错，看着值钱的先抢！

那么问题很简单咯 ，把” 值钱” 的东西排在前面，每次拿抢
的时候，问问看背包君够不够承受得住，承受的了，就全部抢过
来。承受不住，那么只能按照所能承受的重量，取物品的一部分
了。当然价值也得按照比例来哦

部分背包没什么好讲的，主要是一个贪心策略，就是优先选取性价比最高的来装入背包

---

01背包

0 1 背包问题:

有 n 种重量和价值分别为 wi ,vi 的物品，从这些物品中挑选
总重量不超过 W 的物品，求出挑选物品价值总和的最大值。在
这里，每种物品只可以挑选一件

限制条件

• 1≤n≤100 1 ≤ n ≤ 100
• 1≤wi;vi≤100 1 ≤ w i ; v i ≤ 100
• 1≤W≤10000 1 ≤ W ≤ 10000

分析一下

这道题就是各个物品“选”与“不选”的组合，因此被称为0−1背包问题 这 道 题 就 是 各 个 物 品 “ 选 ” 与 “ 不 选 ” 的 组 合 ， 因 此 被 称 为 0 − 1 背 包 问 题 如果检查n个物品所有“选”与“不选”的组合 如 果 检 查 n 个 物 品 所 有 “ 选 ” 与 “ 不 选 ” 的 组 合
算法的复杂度为O(2n) 算 法 的 复 杂 度 为 O ( 2 n ) 当物品的大小以及背包的大小均为正数 当 物 品 的 大 小 以 及 背 包 的 大 小 均 为 正 数
则0−1背包问题可以用动态规划法以O(nW)的效率解决。 则 0 − 1 背 包 问 题 可 以 用 动 态 规 划 法 以 O ( n W ) 的 效 率 解 决 。

状态转移方程：

如果我们按照如下的方式来定义递推关系的话，刚刚关于i的循环就能正向进行 如 果 我 们 按 照 如 下 的 方 式 来 定 义 递 推 关 系 的 话 ， 刚 刚 关 于 i 的 循 环 就 能 正 向 进 行
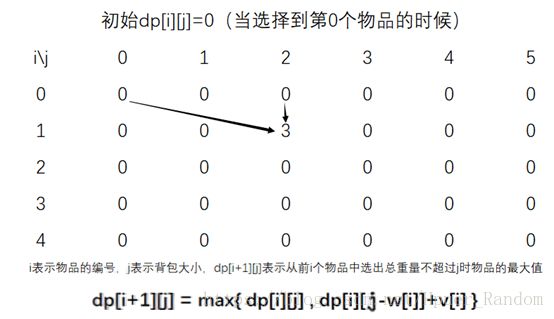
我们定义dp[i+1][j]:=从0到i这i+1个物品中选出总重量不超过 j 的物品时总价值的最大值 我 们 定 义 d p [ i + 1 ] [ j ] := 从 0 到 i 这 i + 1 个 物 品 中 选 出 总 重 量 不 超 过   j   的 物 品 时 总 价 值 的 最 大 值
很显然dp[0][j]=0，因为你没物品可取的时候背包的价值为0 很 显 然 d p [ 0 ] [ j ] = 0 ， 因 为 你 没 物 品 可 取 的 时 候 背 包 的 价 值 为 0

所以我们可以写出下边的状态转移方程

dp[i+1][j]={dp[i][j]max(dp[i][j],dp[i][j−w[i]]+v[i])(j<w[i])其他 d p [ i + 1 ] [ j ] = { d p [ i ] [ j ] ( j < w [ i ] ) m a x ( d p [ i ] [ j ] , d p [ i ] [ j − w [ i ] ] + v [ i ] ) 其他

代码实现1

根据这个状态转移方程我们可以写出这个代码，复杂度 O(nW) O ( n W )

for(int i=0;ifor(int j=0;j<=W;j++)
        if(j1][j]=dp[i][j];
        else
            dp[i+1][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);
printf("%d\n",dp[n][W]);

举个栗子

看一下这个例子

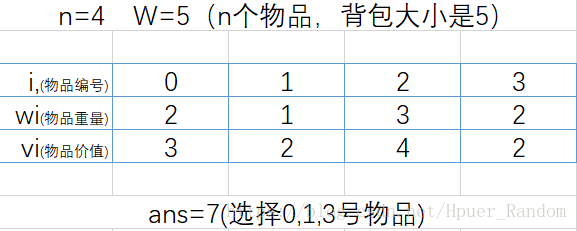
由于你非常优秀, 所以一眼就能够看出来这个问题的答案是多少
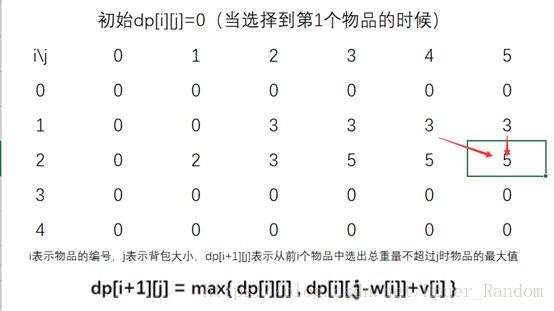
但是我们需要研究一下解决 01 背包的过程中 dp 数组的状态转移过程
所以我们来用这个简单地样例来观察一下 dp 数组的状态是怎么变化的

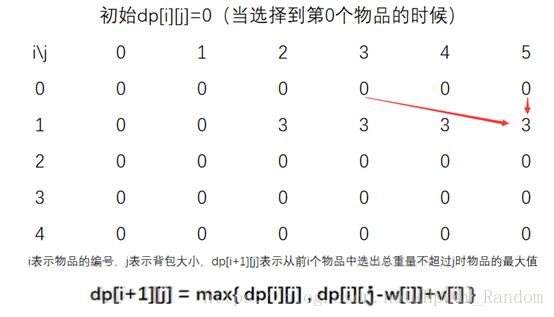
取第 0 个物品 (w0;v0)=(2;3) ( w 0 ; v 0 ) = ( 2 ; 3 )

取第 0 个物品 (w0;v0)=(2;3) ( w 0 ; v 0 ) = ( 2 ; 3 )

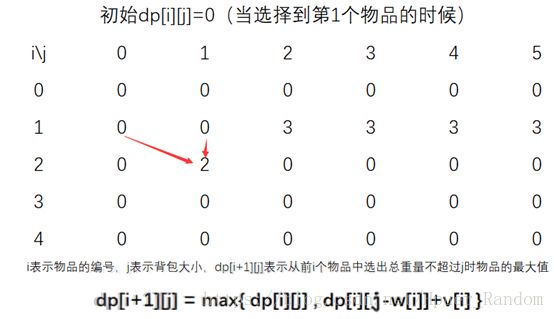
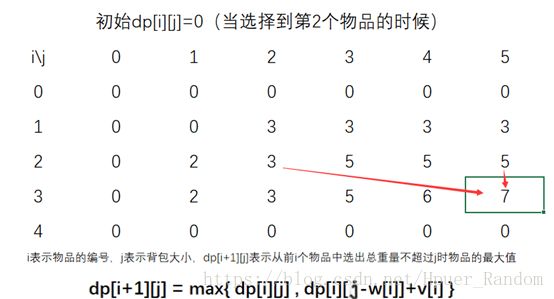
取第1个物品 (w1,v1)=(1,2) ( w 1 , v 1 ) = ( 1 , 2 )

取第1个物品 (w1,v1)=(1,2) ( w 1 , v 1 ) = ( 1 , 2 )

取第1个物品 (w1,v1)=(1,2) ( w 1 , v 1 ) = ( 1 , 2 )

取第1个物品 (w1,v1)=(1,2) ( w 1 , v 1 ) = ( 1 , 2 )

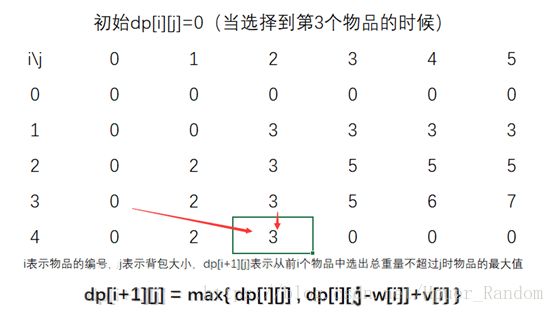
取第2个物品 (w2,v2)=(3,4) ( w 2 , v 2 ) = ( 3 , 4 )

取第2个物品 (w2,v2)=(3,4) ( w 2 , v 2 ) = ( 3 , 4 )

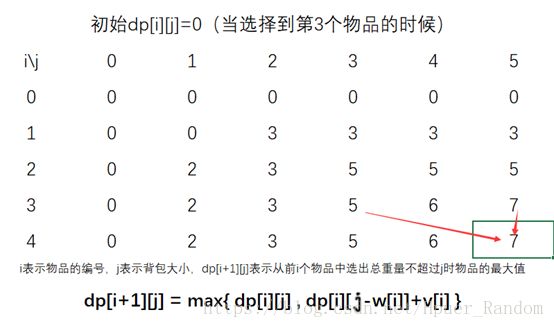
取第3个物品 (w3,v3)=(2,2) ( w 3 , v 3 ) = ( 2 , 2 )

取第3个物品 (w3,v3)=(2,2) ( w 3 , v 3 ) = ( 2 , 2 )

再啰嗦一下

希望大家能够根据上边的例子完全的理解01背包的实现过程，因为01背包非常重要的，它是背包问题的基础，基础牢固对其他动态规划的学习也有帮助的。

01背包代码实现2

• 此外，01背包的还可以通过两个数组滚动来实现重复利用

int dp[2][MAXN];
for(int i=0;i<n;i++)
    for(int j=0;j<=W;j++)
       if(j<w[i])
          dp[(i+1)&1][j]=dp[i&1][j];
       else
  dp[(i+1)&1][j]=max(dp[i&1][j],dp[i&1][j-w[i]]+v[i]);

printf("%d\n",dp[n&1][W]);

01背包代码实现3

• 当然，还可以通过不断重复用一个数组来实现

int dp[MAXN];
for(int i=0;ifor(int j=W;j>=w[i];j--)
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
printf("%d\n",dp[W]);

---

完全背包

问题提出

有n种重量和价值分别为 有 n 种 重 量 和 价 值 分 别 为 w[i],v[i] 的物品 的 物 品
从这些物品中挑选总重量不超过 从 这 些 物 品 中 挑 选 总 重 量 不 超 过 W 的物品 的 物 品
求出挑选物品价值总和的最大值。在这里，每种物品可以挑选任意件 求 出 挑 选 物 品 价 值 总 和 的 最 大 值 。 在 这 里 ， 每 种 物 品 可 以 挑 选 任 意 件

• 限制条件
  
  • 1≤n≤100 1 ≤ n ≤ 100
  • 1≤wi,vi≤100 1 ≤ w i , v i ≤ 100
  • 1≤W≤10000 1 ≤ W ≤ 10000

递推关系

这次同一类的物品可以挑选任意多件了。我们再试着写出递推关系。 这 次 同 一 类 的 物 品 可 以 挑 选 任 意 多 件 了 。 我 们 再 试 着 写 出 递 推 关 系 。
令 dp[i+1][j]=从前i种物品中挑选总重量不超过 j 时总价值的最大值。那么递推关系就为： 令   d p [ i + 1 ] [ j ] = 从 前 i 种 物 品 中 挑 选 总 重 量 不 超 过   j   时 总 价 值 的 最 大 值 。 那 么 递 推 关 系 就 为 ：

dp[0][j]=0 d p [ 0 ] [ j ] = 0

dp[i+1][j]=max{dp[i][j−k∗w[i]]+k∗v[i]|0<=k} d p [ i + 1 ] [ j ] = m a x { d p [ i ] [ j − k ∗ w [ i ] ] + k ∗ v [ i ] | 0 <= k }

如果按照这个递推关系来写程序话，代码是这样子的：

• 完全背包代码实现1

for(int i=0;ifor(int j=0;j<=W;j++)
        for(int k=0;k*w[i]<=j;k++)
    dp[i+1][j]=max(dp[i+1][j],dp[i][j-k*w[i]]+k*v[i]);
printf("%d\n",dp[n][W]);

这个代码并不友好，拥有三重循环,时间复杂度是 O(nW2) O ( n W 2 )

上边的代码有很多重复计算，将状态转移方程化简一下 得到的是这样子的

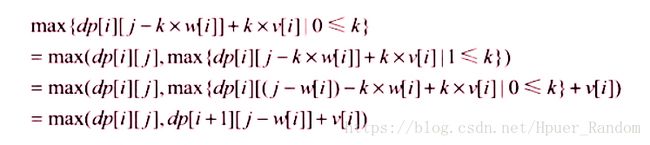
这样一来就不需要k的循环了，便可以用 O(nW) O ( n W ) 时间解决问题

• 完全背包代码实现2

for(int i=0;ifor(int j=0;j<=W;j++)
        if(j1][j]=dp[i][j];
        else
            dp[i+1][j]=max(dp[i][j],dp[i+1][j-w[i]]+v[i]);
printf("%d\n",dp[n][W]);

举个栗子

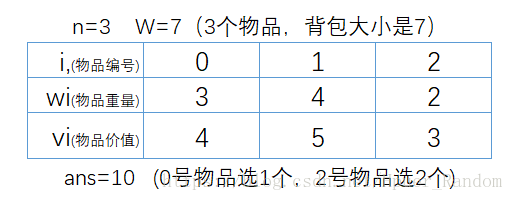
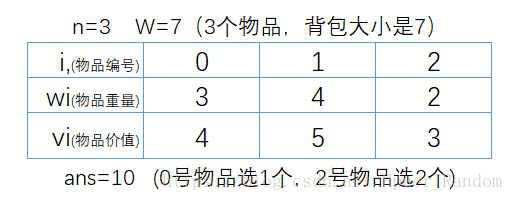
我再来举个栗子
如图所示

你当然能够一眼看出来背包的最大价值是多少 你 当 然 能 够 一 眼 看 出 来 背 包 的 最 大 价 值 是 多 少
为了帮助你理解完全背包状态的转移过程 为 了 帮 助 你 理 解 完 全 背 包 状 态 的 转 移 过 程
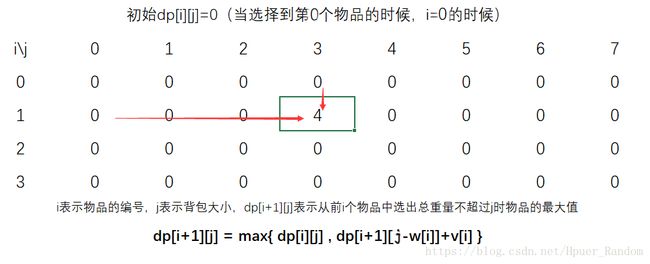
我们可以根据这个例子来看一下dp数组的状态是怎么转移的 我 们 可 以 根 据 这 个 例 子 来 看 一 下 d p 数 组 的 状 态 是 怎 么 转 移 的

取第0个物品 (w0,v0)=(3,4) ( w 0 , v 0 ) = ( 3 , 4 )

取第0个物品 (w0,v0)=(3,4) ( w 0 , v 0 ) = ( 3 , 4 )

取第0个物品 (w0,v0)=(3,4) ( w 0 , v 0 ) = ( 3 , 4 )

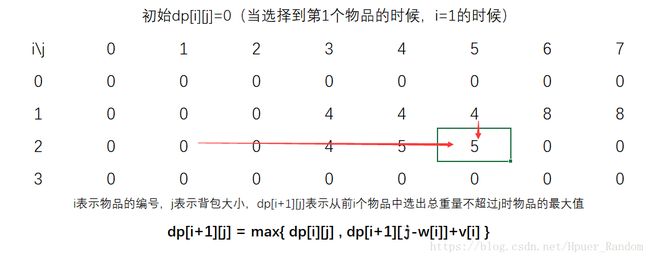
取第1个物品 (w1,v1)=(4,5) ( w 1 , v 1 ) = ( 4 , 5 )

取第1个物品 (w1,v1)=(4,5) ( w 1 , v 1 ) = ( 4 , 5 )

取第2个物品 (w2,v2)=(2,3) ( w 2 , v 2 ) = ( 2 , 3 )

取第2个物品 (w2,v2)=(2,3) ( w 2 , v 2 ) = ( 2 , 3 )

完全背包代码实现2

• 当然我们也可以像01背包那样只开2个二维数组通过滚动来实现数组的重复利用

int dp[2][MAXN];
for(int i=0;i<n;i++)
    for(int j=0;j<=W;j++)
        if(j<w[i])
            dp[(i+1)&1][j]=dp[i&1][j];
        else
dp[(i+1)&1][j]=max(dp[i&1][j],dp[(i+1)&1][j-w[i]]+v[i]);

printf("%d\n",dp[n][W]);

完全背包代码实现3

• 只开一维数组也可以的

int dp[MAXN];
for(int i=0;ifor(int j=w[i];j<=W;j++)
        dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
printf("%d\n",dp[W]);

上边的代码是不是很熟悉？
上边的代码是不是很熟悉？没错，和01背包的代码除了第二个for循环不一样之外，其他的地方一模一样！
为什么会是这个样子呢？

完全背包与01背包关于第二个循环的分析

• 01背包的是第一个的代码，完全背包的是第二个代码

for(int j=W;j>=w[i];j--)
for(int j=w[i];j<=W;j++)

首先我们来想一下为什么 01 背包中要按照j递减的次序来循环。 首 先 我 们 来 想 一 下 为 什 么   01   背 包 中 要 按 照 j 递 减 的 次 序 来 循 环 。
让j递减是为了保证第i次循环中的状态 dp[i][j] 是由状态 dp[i−1][j−w[i]] 递推而来的。 让 j 递 减 是 为 了 保 证 第 i 次 循 环 中 的 状 态   d p [ i ] [ j ]   是 由 状 态   d p [ i − 1 ] [ j − w [ i ] ]   递 推 而 来 的 。
换句话说，这正是为了保证每件物品只选一次，保证在考虑“选入第i件物品”这件策略时， 换 句 话 说 ， 这 正 是 为 了 保 证 每 件 物 品 只 选 一 次 ， 保 证 在 考 虑 “ 选 入 第 i 件 物 品 ” 这 件 策 略 时 ，
依据的是一个绝无已经选入第i件物品的子结果 dp[i−1][j−w[i]] . 依 据 的 是 一 个 绝 无 已 经 选 入 第 i 件 物 品 的 子 结 果   d p [ i − 1 ] [ j − w [ i ] ]   .

• 01背包的是第一个的代码，完全背包的是第二个代码

for(int j=W;j>=w[i];j--)
for(int j=w[i];j<=W;j++)

而现在完全背包的特点恰是每种物品可选无限件 而 现 在 完 全 背 包 的 特 点 恰 是 每 种 物 品 可 选 无 限 件

所以在考虑“加一件第i种物品”这种策略时 所 以 在 考 虑 “ 加 一 件 第 i 种 物 品 ” 这 种 策 略 时

却正需要一个可能已选入第i种物品的子结果dp[i][j−w[i]] 却 正 需 要 一 个 可 能 已 选 入 第 i 种 物 品 的 子 结 果 d p [ i ] [ j − w [ i ] ]

所以就可以并且必须采用v递增的顺序进行循环 所 以 就 可 以 并 且 必 须 采 用 v 递 增 的 顺 序 进 行 循 环

这就是这个简单程序为何成立的道理 这 就 是 这 个 简 单 程 序 为 何 成 立 的 道 理

---

多重背包

问题与应用

有n种重量和价值分别为 w[i]，v[i] w [ i ] ， v [ i ] 的物品，从这些物品中挑选总重量不超过 W W 的物品，求出挑选物品价值总和的最大值。不过在这里，每种物品最多可以挑选 mi m i 件

• 限制条件
  
  • 1≤n≤100 1 ≤ n ≤ 100
  • 1≤wi,vi≤100 1 ≤ w i , v i ≤ 100
  • 1≤mi≤10000 1 ≤ m i ≤ 10000
  • 1≤W≤10000 1 ≤ W ≤ 10000

状态转移方程

dp[i][j]:= 到第i个物品为止总重量不超过j的所有选法中最有可能的最大值 d p [ i ] [ j ] :=  到第i个物品为止总重量不超过j的所有选法中最有可能的最大值

dp[i+1][j]=max(dp[i][j−k∗w[i]]+k∗v[i]|0≤k≤m[i]) d p [ i + 1 ] [ j ] = m a x ( d p [ i ] [ j − k ∗ w [ i ] ] + k ∗ v [ i ] | 0 ≤ k ≤ m [ i ] )

分析分析

对第i种物品有 mi+1 m i + 1 件策略：取0件，取1件…….取 mi m i 件，复杂度是 O(nmW) O ( n m W ) ，无法在规定时间内求解

---

一种好想好写的基本方法是将其转化为01背包问题求解：

把第 i i 件物品换成 mi m i 件01背包中的物品，也就是说：

我们将 mi m i 件物品，变成 0…mi 0 … m i 个物品，

则得到的物品数为 ∑mi ∑ m i 的01背包问题

如果直接求得话，复杂度仍然是 O(nmW) O ( n m W )

---

但是我们希望将它转换成01背包问题之后，能够想完全背包一样降低复杂度。

考虑二进制的思想，把第i件物品换成若干件物品，

使得原问题中的第i件物品可取的每一种策略——取0… mi m i 件

均能够等价于取若干件物品代换之后后的物品，另外，取 mi m i 件的策略必不能够出现

---

将 mi m i 分解为如下形式:

mi=1+2+4+⋯+2k+a(0≤a≤2k+1) m i = 1 + 2 + 4 + ⋯ + 2 k + a ( 0 ≤ a ≤ 2 k + 1 )

由于 1,2,…,2k 1 , 2 , … , 2 k 的组合可以表示出 0⋯2k+1−1 0 ⋯ 2 k + 1 − 1 的所有整数，因此 1,2,⋯2k,a 1 , 2 , ⋯ 2 k , a 可以表示出所有 0 mi 0   m i 的所有整数

因此，我们把 mi m i 个重量和价值分别为 wi w i 和 vi v i 的物品，
看成重量和价值分别为 wi∗x,vi∗x(x=1,2,⋯,2k,a) w i ∗ x , v i ∗ x ( x = 1 , 2 , ⋯ , 2 k , a ) 的 k+2 k + 2 个物品。

这样，物品的总个数就变为 O(nlog m) O ( n l o g   m ) 个，
使用一般的01背包DP可以在 O(nWlogm) O ( n W l o g m ) 时间内求出答案

---

举个栗子

比如说给我的第i个物品，重量为2，价值100，数量13；
按照上边二进制的形式将13分解之后 13=1+2+4+6 13 = 1 + 2 + 4 + 6 所以我们就得到了4个物品，这四个物品分别是

系数	重量w	价值v	备注
1	2	100	1个i
2	4	200	2个i
4	8	400	4个i
6	12	600	6个i

我们可以通过对这四个物品取或者不取
可以达到对第i个物品取 0,1,2⋯13 0 , 1 , 2 ⋯ 13 件的操作
所以我们的目的就达成了，将其变成01背包的问题！

多重背包代码实现

for(int i=0;iint num=m[i];//用来找a 
    for(int k=1;num>0;k<<=1){
        int mul=min(k,num);
        for(int j=W;j>=w[i]*mul;j--){
            dp[j]=max(dp[j],dp[j-w[i]*mul]+v[i]*mul); 
        }
        num-=mul;
    }
}
printf("%d\n",dp[W]);

---

个人拙见，如果有错误请在留言区指出
emmm，希望对大家学习背包有所帮助