bzoj3091：城市旅行 （LCT+期望值）

题目传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=3091
题目分析：这题是LCT半裸题吧（1A好爽）。这题的前三个操作都是很常见的LCT的操作，但第四个操作……什么鬼？
假设我们取出u->v的路径来做暴力，设长度为len。答案等于：

∑lenx=1∑leny=xH(x,y)len(len+1)2

---

现在我们考虑如何在splay上维护分子分母。很明显，分母我们只要维护一个Size即可，但如果我们只是直接维护分子（记为val）是不能够进行区间信息合并的。我们把区间一分为二，整段的val等于左半段的val+右半段的val+（当x在左半边[1,mid]，y在右半边[mid+1,R]的情况）。
那么括号内的东西怎么维护呢？我们假设枚举x，看看x=1~mid时分别对val有什么贡献：

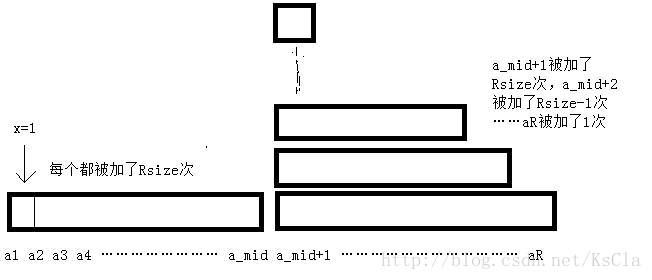
上面就是当x=1，y从mid+1扫到R时对val的贡献。

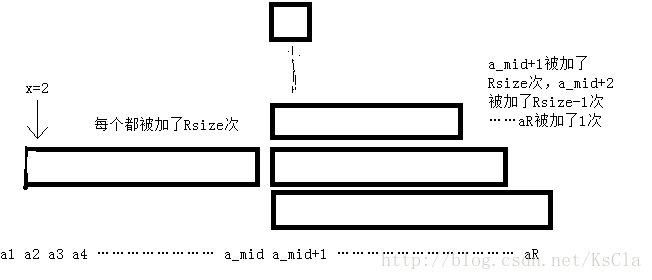
上面是x=2时的情形。
接下来就不再枚举了，我们已经很容易YY出接下来的情形。
于是最后就变成了：

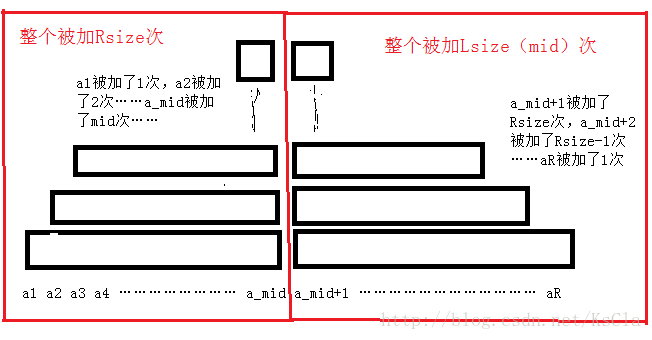
接下来要做什么就很明朗了：我们再额外维护两个域：Left=a1*1+a2*2+……+a_Size*Size；Right=a1*Size+a2*(Size-1)+……a_Size*1。然后合并的时候用这两个信息随便搞搞，val就被维护好了。而且很明显这两个信息是可以通过再维护一个sum=a1+a2+……a_Size维护好的。

---

然后我们考虑懒惰标记对每一个域的影响。翻转标记flip除了会令Left和Right互换以外，没什么别的麻烦之处。重点在于add标记。首先它会令Left和Right各加[Size*(Size+1)/2]*add（看看上面的图就知道了），那么它会令val加多少呢？
我们换一种角度思考问题：我们要在[1,Size]里选出一个区间[x,y]，长度为1的选法有Size种，长度为2的选法有Size-1种……。而长度为x的区间，每一个数加add之后，会令val加x*add，于是：

val+=add∗∑x=1Sizex(Size+1−x)

整理得：

val+=add∗(∑x=1Sizex(Size+1)−∑x=1Sizex2)

然后就可以O(1)地求了对吧？（平方前缀和公式请自行脑补）

---

CODE：

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;

const int maxn=50010;
typedef long long LL;

struct Tnode;
void Get(Tnode *,Tnode *,Tnode *);
void Add(LL ,Tnode *);

struct Tnode
{
    LL num,sum,val,Left,Right,add;
    int Size,path_parent;
    bool flip;
    Tnode *fa,*son[2];
    int Get_d() { return fa->son[1]==this; }
    void Connect(Tnode *P,int d) { (son[d]=P)->fa=this; }
    void Up()
    {
        sum=val=Left=Right=num;
        Size=1;
        if (son[0]) Get(this,son[0],this);
        if (son[1]) Get(this,this,son[1]);
    }
    void Push_down()
    {
        if (flip)
        {
            swap(son[0],son[1]);
            if (son[0]) swap(son[0]->Left,son[0]->Right),son[0]->flip^=1;
            if (son[1]) swap(son[1]->Left,son[1]->Right),son[1]->flip^=1;
            flip=false;
        }
        if (add)
        {
            if (son[0]) Add(add,son[0]);
            if (son[1]) Add(add,son[1]);
            add=0;
        }
    }
} tree[maxn];
Tnode *Node[maxn];
int cur=-1;

void Get(Tnode *P,Tnode *L,Tnode *R)
{
    P->val=L->val+R->val+L->Right*R->Size+L->Size*R->Left;
    P->Left=L->Left+R->Left+L->sum*R->Size;
    P->Right=L->Right+R->Right+L->Size*R->sum;
    P->Size=L->Size+R->Size;
    P->sum=L->sum+R->sum;
}

LL Sum(LL len)
{
    LL x=len*(len+1LL)/2LL;
    LL y=len*(len+1LL)*(2LL*len+1LL)/6LL;
    return x*(len+1LL)-y;
}

void Add(LL a,Tnode *P)
{
    P->num+=a;
    P->sum+=( (long long)P->Size*a );
    P->val+=( Sum(P->Size)*a );
    LL x=(long long)P->Size*(long long)(P->Size+1)/2LL;
    P->Left+=(x*a);
    P->Right+=(x*a);
    P->add+=a;
}

int n,m;

Tnode *New_node(LL a)
{
    cur++;
    tree[cur].num=tree[cur].sum=tree[cur].val=tree[cur].Left=tree[cur].Right=a;
    tree[cur].add=tree[cur].path_parent=tree[cur].flip=0;
    tree[cur].Size=1;
    tree[cur].fa=tree[cur].son[0]=tree[cur].son[1]=NULL;
    return tree+cur;
}

void Update(Tnode *P)
{
    if (!P) return;
    Update(P->fa);
    P->Push_down();
}

void Zig(Tnode *P)
{
    int d=P->Get_d();
    Tnode *F=P->fa;
    if (P->son[!d]) F->Connect(P->son[!d],d);
    else F->son[d]=NULL;
    if (F->fa) F->fa->Connect(P,F->Get_d());
    else P->fa=NULL;
    F->Up();
    P->Connect(F,!d);
    P->path_parent=F->path_parent;
    F->path_parent=0;
}

void Splay(Tnode *P)
{
    Update(P);
    while (P->fa)
    {
        Tnode *F=P->fa;
        if (F->fa) ( P->Get_d()^F->Get_d() )? Zig(P):Zig(F);
        Zig(P);
    }
    P->Up();
}

void Down(int x)
{
    Splay(Node[x]);
    Tnode *&tag=Node[x]->son[1];
    if (tag)
    {
        tag->fa=NULL;
        tag->path_parent=x;
        tag=NULL;
        Node[x]->Up();
    }
}

void Access(int x)
{
    Down(x);
    int y=Node[x]->path_parent;
    while (y)
    {
        Down(y);
        Node[y]->Connect(Node[x],1);
        Node[y]->Up();
        Node[x]->path_parent=0;
        x=y;
        y=Node[x]->path_parent;
    }
}

void Evert(int x)
{
    Access(x);
    Splay(Node[x]);
    Node[x]->flip^=1;
    swap(Node[x]->Left,Node[x]->Right);
}

void Link(int x,int y)
{
    Evert(x);
    Splay(Node[x]);
    Node[x]->path_parent=y;
}

Tnode *Find_root(Tnode *P)
{
    if (!P->son[0]) return P;
    return Find_root(P->son[0]);
}

LL Gcd(LL x,LL y)
{
    if (xif (!y) return x;
    return Gcd(y,x%y);
}

int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);

    scanf("%d%d",&n,&m);
    for (int i=1; i<=n; i++)
    {
        int a;
        scanf("%d",&a);
        Node[i]=New_node(a);
    }
    for (int i=1; iint u,v;
        scanf("%d%d",&u,&v);
        Link(u,v);
    }

    for (int i=1; i<=m; i++)
    {
        int id,u,v;
        scanf("%d%d%d",&id,&u,&v);

        if (id==1)
        {
            Evert(u);
            Access(v);
            Splay(Node[v]);
            if ( Find_root(Node[v])!=Node[u] ) continue;
            Splay(Node[u]);
            if ( Find_root(Node[u]->son[1])!=Node[v] ) continue;
            Tnode *&tag=Node[u]->son[1];
            if (tag)
            {
                tag->fa=NULL;
                tag->path_parent=0;
                tag=NULL;
                Node[u]->Up();
            }
        }

        if (id==2)
        {
            Evert(u);
            Access(v);
            Splay(Node[v]);
            if ( Find_root(Node[v])==Node[u] ) continue;
            Link(u,v);
        }

        if (id==3)
        {
            int d;
            scanf("%d",&d);
            Evert(u);
            Access(v);
            Splay(Node[v]);
            if ( Find_root(Node[v])!=Node[u] ) continue;
            Add(d,Node[v]);
        }

        if (id==4)
        {
            Evert(u);
            Access(v);
            Splay(Node[v]);
            if ( Find_root(Node[v])!=Node[u] ) printf("-1\n");
            else
            {
                LL x=Node[v]->Size;
                x=x*(x+1LL)/2LL;
                LL gcd=Gcd(Node[v]->val,x);
                printf("%I64d/%I64d\n",Node[v]->val/gcd,x/gcd);
            }
        }
    }

    return 0;
}