Real-time 3D Hand Pose Estimation with 3D Convolutional Neural Networks
基于三维卷积神经网络的实时三维手势估计
1 摘要
在本文中,我们提出了一种使用三维卷积神经网络(CNNs)从单深度图像进行实时三维手姿态估计的新方法。2D CNN提取的基于图像的特征由于缺乏3D空间信息,不适合直接进行3D手姿势估计。我们提出的基于3D CNN的方法,将手部深度图像的3D体积表示作为输入并从体积输入中提取3D特征,可以捕获手的3D空间结构并且在单通道中准确地回归全3D手部姿势。为了使3D CNN对手部大小和全局方向的变化具有鲁棒性,我们对训练数据执行3D数据增强。为了进一步提高估计精度,我们建议应用3D深度网络架构并利用完整的手部表面作为从深度图像学习3D手部姿势的中间监督。对三个具有挑战性的数据集进行了大量实验,结果表明我们提出的方法优于基线和最先进的方法。交叉数据集实验也表明我们的方法具有良好的泛化能力。此外,我们的方法很快,在具有单个GPU的标准计算机上以每秒超过91帧的速度运行。
2 介绍
随着实时人体姿势估计的成功[1],[2],[3]以及中距离和短距离深度相机的可用性,如英特尔实感,SoftKinetic和Primesense Carmine,近年来,准确时实3D手部姿态估计引起了很多研究的关注[4],[5],[6],[7],[8],[9],[10],[11],[12]。铰接式3D手姿态估计是虚拟现实和增强现实应用中人机交互的核心技术之一,因为该技术为用户提供了与虚拟环境和虚拟对象交互的自然方式。3D手姿势估计也可以用于手势识别,例如手语识别[13],[14]和驾驶员手势分析[15],[16]。然而,由于手部姿势的大变化,手部运动的高维度,严重的自我遮挡以及深度图像中的手指的自相似性,实现有效且稳健的手部姿势估计性能仍然是具有挑战性的。
由于卷积神经网络(CNNs)的成功[7],[17],[18],[19],[20],[21],[22],[23],[24],[25]和大型手姿势数据集的可用性[7],[8],[26],近期许多手势估计工作取得了良好的效果。大多数这些方法直接将深度图像作为2D CNN的输入,输出热图[7](图1a),3D关节位置[17],[18],[20],[21],[24](图1c)或手模型参数[22]。然而,我们认为由于缺乏3D空间信息,由2D CNN提取的基于图像的特征不直接适合于3D手姿势估计。例如,在[18]中,2D CNN的初始结果很差,并且它被反馈循环迭代地重新定义以合并来自生成模型的3D信息。Ge等人[19]通过将深度图像投影到三个视图上并应用多视图CNN来回归三个视图的热图(图1b),从而更好地利用深度线索。然而,多视图CNN仍然不能充分利用深度图像中的3D空间信息,因为从3D到2D的投影将丢失某些信息。虽然增加视图的数量可以改善性能,但是当使用更多视图时,计算复杂性将增加。

图1:3D手姿势估计的不同方案。(a)2D CNN将深度图像作为输入并输出热图。(b)多视图2D CNN将多视图投影作为输入并输出多视图热图。(c)2D CNN将深度图像作为输入并直接回归3D关节位置。(d)我们使用3D CNN,其采用体积表示作为输入并且回归3D关节位置的较低维度表示。
在本文中,我们提出了一种基于3D CNN的手姿势估计方法,该方法可以捕获输入的3D空间结构,并在单通道中准确地回归全3D手势,如图1d所示。具体而言,人手首先从深度图像中分割出来;手的3D点云被编码为3D体积存储投影方向截断有符号距离函数(D-TSDF)[27]值,然后将其馈送到3D卷积神经网络中。我们设计了一个3D深度密集网络,以提高网络的学习能力。该网络的输出是3D手部关节在3D体积中的相对位置的较低维度表示。通过执行PCA重建和坐标转换,我们可以最终获得相机坐标系中的3D手部关节位置。通过3D卷积提取的3D特征的优势,我们的方法能够理解3D空间中的手姿态结构,并且能够有效且稳健地推断3D手部关节位置。
与先前基于CNN的手姿态估计方法相比,我们提出的基于3D CNN的方法具有以下优点:
- 我们提出的3D CNN能够从3D体积表示中学习3D特征,以进行精确的3D手姿势估计。与从2D特征回归3D关节位置的基于2D CNN的方法相比[17],[18],[21],[28],3D CNN可以在单通道中直接从3D特征回归3D关节位置。这不仅实现了卓越的估计精度,而且避免了耗时的迭代重建过程。
- 我们提出的3D CNN可以轻松地以端到端的方式进行训练。我们在本文中设计的3D浅平面网络和3D深度密集网络都可以在单个GPU上以实时速度运行。
- 我们提出的方法对手部大小和全局方向的变化具有鲁棒性,因为我们在训练集上执行3D数据增强。与在2D图像上执行2D变换的传统数据增强不同,我们提出的3D数据增强在3D点云上应用3D变换,因此可以更好地丰富3D空间中的训练数据。
本文是我们会议论文的延伸[29]。本文的新贡献总结如下:
- 我们已经提出利用完整的手部表面作为从深度图像学习3D手部姿势的中间监督。实验结果表明,利用中间手表面补全步骤,可以进一步提高3D手姿态的估计精度。
- 我们已经研究了深度神经网络架构的性能[30],[31],当应用于我们提出的基于3D CNN的3D手姿态估计框架时,以提高学习能力。 实验结果表明,3D深层网络可以实现比3D浅层网络更好的性能。
- 为了更好地理解3D CNN,我们已经可视化了在3D特征体积中产生给定激活的输入方案。在这些方案中已经观察到手的局部和全局3D结构。
- 我们进行了更广泛的自身比较实验,并在一个额外的手姿势数据集ICVL上与更多最先进的方法进行了比较[8]。我们还进行了跨数据集实验,并与英特尔实感SDK进行了定性比较[32]。实验结果表明,该方法可以实时获得良好的性能,具有良好的泛化能力。
本文的其它部分组织如下:第2节讨论了3D手姿态估计的一些相关工作。由于我们的方法以3D体积为输入,我们首先在第3节介绍不同的体积表示,然后第4节描述所提出的基于3D CNN的方法。第5节提供了实验结果,第6节总结了本文。
3 体积表示
我们提出的基于3D CNN的手姿态估计方法采用体积表示作为神经网络的输入。将观察到的手部深度图像编码为体积表示的目的是生成3D体积,从深度图像实时提供3D空间中的手的充分且有意义的信息。3D体积将被馈送到3D CNN以学习3D特征以用于随后的3D手部关节位置回归。
手的输入深度图像首先被转换为一组3D点,表示为 P ⊂ R 3 P\subset\mathbb{R}^3 P⊂R3,如图2的前两行所示。为了创建包含 M × M × M M×M×M M×M×M体素的3D体积,我们首先为3D手点构建轴对齐边界框(AABB)。AABB是最小边界框,其x,y,z轴分别与摄像机坐标系的x,y,z轴对齐。3D体积的中心设置在AABB的中心,其面设置为与AABB的面平行。体素的边长度设置为:
l v o x e l = m a x l x , l y , l z / M ( 1 ) l_{voxel} = max{l_x, l_y, l_z} / M \qquad (1) lvoxel=maxlx,ly,lz/M(1)
其中lx,ly,lz是AABB沿三个方向的边长;M是体积分辨率值。我们将体素v的值表示为F(v),可以通过使用占用模型(第3.1节)或截断符号距离函数(第3.2节)来确定。

图2:不同体积表示的可视化。对于最后五行,我们仅通过使用此图中所示的颜色映射来显示其值小于1且大于-1的体素。体积分辨率为32×32×32。
3.1 占据栅格
占据栅格是表示3D体积中的占用和未占用体素的二进制栅格,如图2的第3行所示。因此,体素值被确定为:
F ( v ) = { 1 ∃ p ∈ P , s . t . D C h e ( v c , p ) ≤ l v o x e l / 2 0 o t h e r w i s e ( 2 ) F(v) = \begin{cases} 1 & \exists p \in P,s.t.D_{Che} (v_c, p) \le l_{voxel / 2} \\ 0 & otherwise \\ \end{cases} \qquad (2) F(v)={10∃p∈P,s.t.DChe(vc,p)≤lvoxel/2otherwise(2)
其中 D C h e ( p , q ) = max i ( ∣ p i − q i ∣ ) D_{Che} (p, q) = \max\limits_i (| p_i - q_i |) DChe(p,q)=imax(∣pi−qi∣)是Chebyshev距离; v c v_c vc是体素v的中心。
如果输入是完全已知3D信息的3D CAD模型,则占据栅格足以表示完整的3D模型。 然而,在我们的问题中,输入是2.5D深度图像,其仅从相机的视图捕获观察到的表面点,这是手的不完整的3D形状。占据栅格不能区分观察到的表面前和后的体素。
3.2 TSDF体积
在基于精确的截断符号距离函数(TSDF)的体积中,每个体素存储从体素中心到最近的表面点的截断有符号距离。体素v的值计算如下:
F ( v ) = m i n m a x d ( v c ) / μ , − 1 , − 1 ( 3 ) F(v) = min {max {d(v_c) / \mu, -1}, -1} \qquad (3) F(v)=minmaxd(vc)/μ,−1,−1(3)
其中 d ( v c ) d(v_c) d(vc)是从体素中心 v c v_c vc到最近表面点的符号距离;当体素中心的深度值小于最近表面点的深度值时,其符号为正;否则,符号为负。 μ \mu μ是截断距离,此处设置为 3 × l v o x e l 3×l_{voxel} 3×lvoxel。
但是,计算精确的TSDF非常耗时,因为必须检查所有表面点以找到3D体积中每个体素的最近点。对于实时考虑,应该使用投影TSDF[58],其中最近的点仅在相机帧中的视线上找到。它可以在GPU上有效地并行计算。由于投影TSDF是精确TSDF的近似,因此在投影TSDF中一些信息是不准确的或丢失的。在这项工作中,我们应用投影方向TSDF(D-TSDF)[27]来编码体积表示中的更多信息,其中每个体素将3D偏移矢量 [ d x , d y , d z ] [dx, dy, dz] [dx,dy,dz]存储到最近点而不是标量距离。
图2(最后五行)显示了一些例子:准确的TSDF体积,投射TSDF体积和具有不同手部姿势的投影D-TSDF体积。可以看出,在准确的TSDF体积中,TSDF的值在从观察到的表面移动到自由空间时增加,而在移动到被遮挡的空间时减小。在投影TSDF体积中,TSDF的值沿着视线连续变化,其在观察到的表面前面保持为正,在观察到的表面后面保持为负。 z方向的投影D-TSDF体积与投影TSDF体积几乎相同,因为z方向接近视线。x,y方向的投影D-TSDF体积可以提供更多信息以补偿投影TSDF体积的不准确性。第5.3.2节中的实验将表明投影D-TSDF在计算上是有效的,并且可以提高估计精度。
我们需要在预测精度和计算成本之间取得平衡,以确定体积分辨率 M M M。如果体积分辨率太大,则计算体积表示将是耗时且占用大量内存的。如果体积分辨率太小,则体积表示无法为3D手部姿势估计提供足够的信息。在这项工作中, M M M被选为32,根据第5.3.1节中的实验证明其具有良好的估计精度和3D手姿态估计的计算效率。
4 3D卷积神经网络
在本节中,我们首先描述了用于3D手姿态回归的网络架构和损失函数。为了解决自遮挡和全局方向的大变化问题,我们进一步介绍了3D手部表面补全和3D数据增强的方法。在本节的最后,我们可视化和分析3D CNN学习的3D模式。
4.1 网络架构
我们提出的3D CNN将三个体积的投影D-TSDF作为输入并输出包含F个元素的矢量。如图3所示,我们设计了两种网络架构:3D浅平面网络和3D深度密集网络。
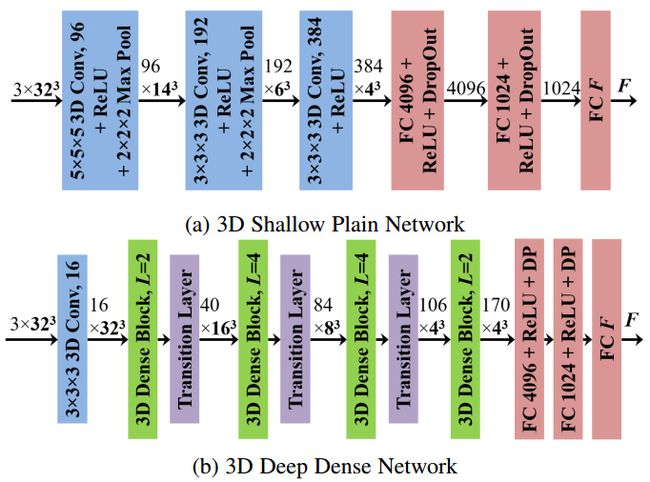
图3:简单和密集的网络架构。两个网络都采用三个32×32×32投影D-TSDF体积作为输入和输出F元素。在(a)中,所有3D卷积层都具有步幅1且没有填充。在(b)中,3D深密网络的增长率为32;每个3D密集块中的L表示密集单元的数量;每个密集单元由一系列层组成:BN-ReLU-3D Conv(1×1×1)-BN-ReLU-3D Conv(3×3×3);每个过渡层使用1×1×1 3D卷积将特征图的数量减少一半,并使用平均合并对特征图进行下采样。'BN’表示批量标准化层,'FC’表示完全连接的层,'DP’表示丢失层。
4.1.1 3D浅平网络
3D浅平面网络包含三个3D卷积层和三个完全连接的层,如图3a所示。对于三个3D卷积层,内核大小为 5 3 5^3 53, 3 3 3^3 33和 3 3 3^3 33,步长都为1且没有填充。前两个3D卷积层之后是3D最大池层,内核大小为 2 3 2^3 23,步长为2且没有填充。在通过3D卷积层提取3D特征之后,使用三个完全连接的层将3D特征映射到3D手部关节位置的较低维度空间。在前两个完全连接的层中,我们应用具有0.5的丢弃率的丢弃层,以防止神经网络过拟合[59]。
4.1.2 3D深密网络
具有捷径的深度卷积网络已经显示出强大的图像识别学习能力[30],[31],因为捷径可以缓解梯度消失问题。我们在提出的基于3D CNN的手姿态估计方法中应用深密网络架构[31]。如图3b所示,我们设计了一个包含28个卷积层和3个完全连接层的3D深度密集网络。遵循[31]中的体系结构,我们在每个密集块中应用瓶颈层以减少模型参数的数量。5.3.5节的实验表明,与3D浅平面网络相比,3D深度密集网络可以获得更准确的估计结果。
4.2 3D手势回归的损失函数
我们的方法估计3D空间中的 K K K个手关节位置,其表示3D手姿势。设K个目标手关节位置为 Φ = { Φ k } k = 1 K ∈ Λ \varPhi = \{\varPhi_k\}^K_{k =1} \in Λ Φ={Φk}k=1K∈Λ里 Λ Λ Λ是 3 × K 3×K 3×K维手关节空间。我们将训练样本表示为 ( X n , Φ n ) (X_n, Φ_n) (Xn,Φn),其中 X n X_n Xn是深度图像, Φ n Φ_n Φn是摄像机坐标系中对应的关节位置, n = 1 , . . . . , N n = 1, ...., N n=1,....,N。深度图像 X n X_n Xn被转换为体积表示 V n V_n Vn,如第3节中所述。 V n V_n Vn的中心位于从3D手点生成的AABB的中心。因此,真实值 Φ n Φ_n Φn应该转换为体积坐标系中的坐标,并在0和1之间归一化。我们将变换和归一化的关节位置表示为 Y n = { y n k } k = 1 K ∈ Λ Y_n= \{ynk\}^K_{k=1} \in Λ Yn={ynk}k=1K∈Λ。将第k个手关节的3D位置 y n k ∈ R 3 y_{nk} \in \mathbb{R}^3 ynk∈R3变换并归一化为:
y n k = ( ϕ n k − c n ) / ( M ⋅ l v o x e l ) + 0.5 ynk = (\phi_{nk} - c_n) / (M \centerdot l_{voxel}) + 0.5 ynk=(ϕnk−cn)/(M⋅lvoxel)+0.5
其中 c n c_n cn是3D体积的中心。通过减去中心 c n c_n cn将原始真是值位置 φ n k φ_{nk} φnk转换为体积坐标系,并通过除以体积的边长 l v o x e l l_{voxel} lvoxel(我们假设所有关节都在3D体积内)将其归一化在-0.5和0.5之间。为了使 y n k y_{nk} ynk的坐标在0和1之间,我们在这个公式中加0.5。
由于3D手关节的自由度(DOF)通常低于手关节位置的维度 3 × K 3×K 3×K,我们设计的3D CNN明确强制手部关节位置估计的手部设置约束,因此可以减轻手姿势估计不可行性。为了学习手姿势先验,我们在训练数据集中对变换和归一化的关节位置 { Y n } n = 1 N \{Y_n\}^N_{n=1} {Yn}n=1N执行PCA,这与[17]中的方法类似。主成分的系数是 α n = E T ⋅ ( Y n − u ) α_n=E^T·(Y_n -u) αn=ET⋅(Yn−u),其中 α n α_n αn包含 F F F个系数, F < 3 × K ; E = [ e 1 , e 2 , . . . , e F ] F<3×K;E = [e_1,e_2, ..., e_F] F<3×K;E=[e1,e2,...,eF]是主要成分; u u u是 Y Y Y的平均向量。
在训练阶段,我们使用SGD算法最小化以下目标函数:
w ∗ = a r g min w ∑ n = 1 N ∣ ∣ α n − F ( V n , w ) 2 ∣ ∣ ( 5 ) w^* = arg \min\limits_w \sum^N_{n=1}|| \alpha_n - F(V_n,w)^2 || \qquad (5) w∗=argwminn=1∑N∣∣αn−F(Vn,w)2∣∣(5)
在测试阶段,给定输入体积表示 V V V,由3D CNN估计的变换和归一化的手关节位置是 Y ^ = E ⋅ F ( V , w ∗ ) + u \hat{Y} = E·F(V, w^*)+ u Y^=E⋅F(V,w∗)+u。
4.3 手部表面补全
3D手姿势估计中的挑战之一是输入深度图像仅捕获部分手表面并且遭受自遮挡问题。为了解决这个问题,我们利用完整的手部表面作为中间监督,从深度图像学习3D手部姿势。更具体地说,我们使用数据驱动方法估计完整的手部表面,并利用估计的完整手部表面进行3D手部姿势估计。如图4所示,我们应用3D U-Net[61]架构来估计捕获的部分手部表面的完整手部表面。与[62]类似,我们使用无符号截断距离函数(TDF)作为网络输出,因为没有必要区分完整手表面的距离函数的已知和未知空间。通过使用具有3D手模型的模型拟合方法[7]生成完整手部表面的真实值。在训练3D U-Net时,我们使用ADAM优化器[64]最小化[63]中定义的平滑L1损失。在生成完整手部表面的TDF体积之后,我们将其与原始投影D-TSDF体积连接并将它们馈送到3D DenseNet中以进行3D手姿势估计。3D U-Net和3D DenseNet分别进行预培训,并以端到端的方式进行调整。5.3.6节的实验表明,通过手表面补全的中间监督,可以进一步提高3D手姿态估计的准确性。
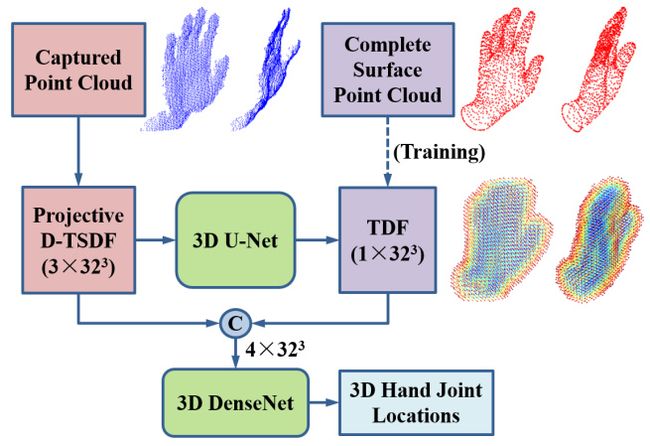
图4:手部表面完成和3D手姿态估计的框架。应用3D U-Net从对应于捕获的部分手表面点的投影D-TSDF体积估计完整手表面点的TDF体积。将与估计的TDF体积连接的投影D-TSDF体积馈送到3D CNN中用于3D手姿势估计。'C’表示连接操作。
4.4 3D数据增强
3D手姿势估计的另一个挑战是手姿势在全局方向和手大小方面具有大的变化。为了使3D CNN模型对不同的方向和大小具有鲁棒性并提高其泛化能力,我们对姿势回归和表面补全网络的训练数据进行3D数据增强。与现有的2D图像数据增强不同,我们的方法直接旋转和拉伸3D空间中的手点。
我们首先沿着相机坐标系的 x x x, y y y, z z z轴拉伸点云,分别用拉伸系数 s x s_x sx, s y s_y sy和 s z s_z sz。然后,点云分别围绕相机坐标系的 x x x, y y y, z z z轴旋转,旋转角度为 θ x θ_x θx, θ y θ_y θy和 θ z θ_z θz。对于3D点 p p p,在拉伸和旋转之后,点 p p p转换为 p ′ p' p′:
p ′ = R ⋅ S ⋅ p R = R x ( θ x ) ⋅ R y ( θ y ) ⋅ R z ( θ z ) ( 6 ) S = D i a g ( s x , s y , s y ) \begin{aligned} &p' = R \centerdot S \centerdot p \\ &R = R_x(\theta_x) \centerdot R_y(\theta_y) \centerdot R_z(\theta_z) \qquad (6)\\ &S = Diag(s_x, s_y, s_y) \end{aligned} p′=R⋅S⋅pR=Rx(θx)⋅Ry(θy)⋅Rz(θz)(6)S=Diag(sx,sy,sy)
其中 R x R_x Rx, R y R_y Ry和 R z R_z Rz分别是围绕 x x x, y y y, z z z轴的3×3旋转矩阵; D i a g ( s x , s y , s y ) Diag(s_x,s_y,s_y) Diag(sx,sy,sy)是3×3对角矩阵,其左上角开始的对角线是 s x s_x sx, s y s_y sy和 s z s_z sz。图5显示了3D数据增强的示例。在手点云和相应的真实值关节位置上执行3D拉伸和旋转。然后从变换后的点云生成TSDF卷。

图5:3D数据增强的示例。左上角:原始点云,真实值和TSDF体积。左下:3D拉伸后的点云,真实值和TSDF体积。右上:三维旋转后的点云,真实值和TSDF体积。右下:3D拉伸和旋转后的点云,真实值和TSDF体积。出于说明目的,我们仅在z方向上绘制投影D-TSDF体积。
在这项工作中,通过随机拉伸和旋转原始训练样本生成增强训练集。拉伸因子 s x s_x sx和 s y s_y sy从区间 [ 1 / 1.5 , 1.5 ] [1/1.5,1.5] [1/1.5,1.5]随机选择对数均匀。由于影响TSDF体积的是相对大小而不是绝对大小,我们可以将伸展因子 s z s_z sz设置为1。在摄像机的坐标系中,从深度图像生成的点云不仅在 z z z内面内旋转,轴也在平面外绕 x x x, y y y旋转,如图5所示。由于点云的不完整性,平面外旋转点云与实际点云不同。我们假设对于小的平面外旋转角度 θ x θ_x θx和 θ y θ_y θy,从平面外旋转点云产生的TSDF体积可以与从实际点云产生的TSDF体积大致相同,此时相机的视点在旋转角度内,我们从区间 [ − 30 ° , 30 ° ] [-30\degree,30\degree] [−30°,30°]随机均匀地选择 θ x θ_x θx和 θ y θ_y θy。从区间 [ − 180 ° , 180 ° ] [-180\degree,180\degree] [−180°,180°]随机均匀地选择面内旋转角度 θ z θ_z θz。在训练阶段,原始训练集和增强训练集都用于训练。第5.3.3节中的实验将显示3D数据增强的有效性。
4.5 可视化3D CNN
为了分析由3D CNN提取的三维特征,我们通过采用[60]中提出的引导反向传播方法,在三维特征体积中可视化产生给定激活的输入模式,该方法是在[65]提出的基于反卷积的可视化方法的修改。
在图6中,我们可视化在3D浅平面网络中学习的一些3D模式,该网络在MSRA手姿势数据集上完全训练[26]。我们采用具有不同手势的三个输入体积作为图6中的示例。为了重建3D模式,通过使用引导的反向传播方法将从3D卷积层生成的3D特征体积向下投射到输入体素空间。对于每个手姿势的每个卷积层,我们选择四个特征体积作为图6中的示例。为了显示输入体积的哪些部分导致3D特征体积中的高激活,我们在3D特征量中最高激活对应的接收域内裁剪重建的3D图案体积。我们还显示了输入3D体积中接收域的相对位置。3D浅平面网络中的第一卷积层(L1),第二卷积层(L2)和第三卷积层(L3)的接收场尺寸分别是5,10和20。

图6:在完全训练的3D CNN模型中学习的模式的可视化。对于每一层,我们在第一行显示重建的模式,并在第二行显示由黑框指示的相应的接收字段。通过使用[60]中提出的引导反向传播方法重建这些模式。对于L3的模式,我们仅绘制绝对值大于阈值的体素。具有较大值的体素以亮色显示,而具有较小值的体素以深色显示。第一卷积层(L1)中的神经元可以捕获局部结构,例如角和边缘;第二卷积层(L2)中的神经元可以捕获手部分的结构,例如手指;第三卷积层(L3)中的神经元可以捕获手的全局结构。
从图6中可以看出,从低层(L1)到高层(L3),神经元可以捕获从局部到全局的模式。L1中的神经元捕获低水平局部几何结构,例如角落(例如,L1列3,8,12)和边缘(例如,L1列1,5,7)。L2中的神经元捕获手的中级形状结构,例如手动手指尖(例如,L2柱5,6,8,10)和手掌边缘(例如,L2柱2,4,7,11)。L3中的神经元捕获手的高级全局结构。值得注意的是,在L3的模式中,手关节区域的对比度是明显的,这表明学习的高层特征体积集中在手关节区域。3D特征的分层特性与[65]中观察到的2D CNN中的分层特性一致。
5 实验
5.1 数据集和评估度量
我们在三个公共手姿势数据集上评估我们提出的方法:MSRA手姿势数据集[26],NYU手姿势数据集[7]和ICVL手姿势数据集[8]。
MSRA数据集[26]包含由英特尔创意互动手势相机捕获的九个受试者的手部深度图像。每个受试者执行17个手势,每个手势包含约500帧。此数据集中有超过76K个帧。在以下关于该数据集的实验中,我们对八个受试者进行训练并对剩余受试者进行测试。对所有受试者重复九次。每个框架的真实值包含K=21个手关节的3D位置,包括每个手指的四个关节和手腕的一个关节。
NYU数据集[7]包含超过72K的训练帧和8K的测试帧,由$PrimeSense^{TM}$3D传感器捕获。每帧的真实值包含36个手关节的3D位置。和[7],[18]中一样,我们估计K=14个手关节的3D位置的子集,包括三个拇指关节,食指,中指,无名指和小指各两个关节,一个关节用于手掌中心和两个手腕关节。由于纽约大学数据集提供了包含人体和背景的原始深度图像,我们应用简化的沙漏网络[66]来检测2D手部关节位置并使用相应的深度信息来分割手部。
ICVL数据集[8]包含12个具有22K帧的训练序列和两个具有1.6K帧的测试序列,由Intel的Creative Interactive Gesture Camera捕获。该数据集另外提供一个训练集,其原始训练样本在平面内旋转14次。然而,在我们的实验中,我们不使用额外的训练集,而是通过随机旋转和拉伸原始训练样本八次来应用3D数据增强。因此,我们实验中的增强训练集包含176K帧。每个帧的真实值包含K=16个手关节的3D位置,包括每个手指的三个关节和手掌中心的一个关节。
在我们的实验中使用三个度量来评估手部姿势估计性能。第一个度量标准是所有测试帧上的每个关节平均误差距离。第二个度量是良好帧的比例,其中最差的关节误差低于阈值[67],这是一个严格的度量。第三个指标是误差阈值内的关节比例[10]。
5.2 实现细节
我们在具有两个Intel Core i7 5930K 3.50GHz CPU,64GB RAM和具有8GB GPU内存的Nvidia GeForce GTX 1080 GPU的计算机上训练和评估我们提出的用于3D手姿态估计的3D CNN模型。3D CNN模型在PyTorch框架内实现。对于网络训练参数,我们选择批量大小为16,动量为0.9,权重衰减为0.0005。对于3D回归网络,学习率设置为0.01,并且在50个周期之后除以10。对于3D U-Net,学习率设置为0.001。在60个周期之后停止训练以防止过拟合。我们对所有数据集上的所有实验应用相同的超参数。 使用[68]中提出的方法随机初始化3D CNN中3D卷积层的所有权重。
5.3 自身比较
5.3.1 选择体积分辨率
为了评估不同体积分辨率的影响,我们使用具有不同分辨率值的投影D-TSDF体积进行实验:使用具有直接回归的3D平面网络的16,32和64。由于以64×64×64分辨率对网络进行训练非常耗时,因此我们仅在MSRA数据集的一小部分上训练和测试具有不同体积分辨率的这三个网络,而在该实验中没有数据增强。如图7(左)所示,16×16×16分辨率的估计精度略低于32×32×32和64×64×64分辨率的估计精度。后两种分辨率的估计精度几乎相同。但是,使用64×64×64分辨率计算TSDF卷更耗时且占用大量内存。因此,体积分辨率32×32×32最适合于手姿态估计,并且我们在以下实验中使用该体积分辨率。该实验还表明,我们的方法对于相对较低的体积分辨率是稳健的,因为当分辨率值为16时,评估精度不会降低很多。

图7:在MSRA数据集上有/无数据增强的不同体积分辨率和不同体积类型的自比较[26]。左:不同体积分辨率对好帧的比例的影响。中:不同卷类型和数据增加对好帧的比例的影响。右:不同体积类型和数据增强对每个关节平均误差距离(R:root,T:tip)的影响。
5.3.2 选择体积类型
我们使用没有数据增强的3D平网络评估不同体积类型对MSRA数据集的估计准确性的影响。从图7(中间和右侧)可以看出,在占据栅格,精确TSDF,投影TSDF和投影D-TSDF中,投影D-TSDF表现最佳。值得注意的是,占据栅格的性能与准确的TSDF和投影TSDF的性能相当,这表明3D CNN可以从占据栅格中学习有效的3D特征,尽管占据栅格不能区分观察表面之前和之后的体素。但投影D-TSDF在三个方向上编码更多信息,优于占据栅格。对于实时性能,在同一GPU上生成占据栅格,精确TSDF,投影TSDF和投影D-TSDF的平均计算时间分别为1.4ms,30.2ms,1.9ms和2.9ms。因此,考虑到估计精度和实时性能,投影D-TSDF总体上是最佳的。在以下实验中,我们应用具有32×32×32体积分辨率的投影D-TSDF作为网络输入并应用3D数据增强用于训练。
5.3.3 评估数据增强
我们比较了不使用数据增强的方法和使用2D/3D数据增强的方法。对于2D数据增强,我们在2D图像平面中随机旋转和拉伸3D手点云。如图7(中间和右侧)所示,当使用相同的输入体积时,使用2D数据增强的方法优于不使用数据增强的方法。当在训练阶段使用3D数据增强时,评估精度进一步提高。值得注意的是,尽管3D旋转点云与真实点云并不完全相同,但使用3D数据增强训练的网络仍然可以获得比使用2D数据增强训练的网络更好的性能,这表明网络可以受益于3D增强数据。
5.3.4 2D CNNs 和3D CNNs比较
我们比较了基于3D CNN的方法和基于2D CNN的方法在实验中的性能。对于基于2D CNN的方法,我们将手从深度图像分割并将其调整为96×96的图像,同时保持纵横比。2D CNN的输出是2D图像手关节的位置和深度值,使用相机参数转换为3D位置。为了公平比较,我们尝试了具有类似网络架构和相当参数数量的2D深密网络和3D深密网络。2D深密网络有5个密集块,29个卷积层和3个具有65M参数的全连接层;3D深度密集网络有4个密集块,28个卷积层和3个具有50M参数的全连接层。此外,我们在训练2D深度密集网络时执行2D数据增强,并且训练样本的数量与训练3D深度密集网络时使用的数量相同。如图8所示,3D深度密集网络在所有三个手势数据集上始终比2D深度密集网络表现更好,这表明3D CNN可以更好地利用深度信息并提供更准确的估计。

图8:在MSRA[26],NYU[7]和ICVL[8]手姿势数据集上进行3D手姿态估计的2D/3D CNN与不同网络架构的自比较。在图例中显示了不同方法的所有关节的平均误差距离。
5.3.5 浅网络和深网络比较
我们比较了3D浅层平面网络和3D深度网络的估计精度。对于3D深度网络,除了深度密集网络之外,我们还尝试了深度残差网络[30],其具有4个残余块,9个卷积层和3个全连接层。从图8可以看出,三维深度密集网络的性能优于三维深度残余网络,三维深度残余网络在三种姿态数据集上的性能优于三维浅层网络。尽管3D深度网络具有更多卷积层,但3D浅平面网络中的卷积层具有更多输出通道。因此,这三个网络的前向传播时间是相当的,3D浅层平面网络为3.5ms,3D深度残余网络为3.4ms,3D深度密集网络为4.5ms。我们在以下实验中使用3D深密网络。
5.3.6 评估手部表面补全
我们评估手部表面补全对3D手姿态估计精度的影响。估计的完整手部表面作为我们方法的中间结果,一些示例在图9中示出。我们使用Matlab的isosurface函数从距离函数的 3 2 3 32^3 323体积中提取手部表面[62]。从图9中可以看出,我们的方法能够从输入的部分手表面生成完整的手部表面。与实际情况相比,我们的估计更加模糊,并且失去了完整手部表面的一些细节。在截断距离为2.5的体素空间中,估计的TDF体积相对于完整表面的真实TDF体积的平均 L 1 L_1 L1损失为0.112。表1给出了使用手部表面补全和不使用手部表面补全的3D手姿态估计的平均误差。可以看出,无论使用3D深度残差网络还是3D深度密集网络,表面补全步骤都可以进一步提高估计准确性。此外,为了评估完整手部表面对手部姿势估计的重要性,我们使用真实的完整手部表面与原始的部分手部表面相结合作为网络输入来估计3D手部姿势。如表1的最后一行所示,当使用完整手部表面的真实值时,网络可以实现小得多的估计误差,这表明如果可以更精确地估计完整的手部表面,我们的方法可以实现更小的姿态估计误差。

图9:使用我们的方法在NYU手姿势数据集上完成手部表面的示例[7]。从 3 2 3 32^3 323体积的距离函数中提取手部表面。
表1:使用3D ResNet和3D DenseNet对手部表面补全对3D手部姿态估计的影响。纽约大学数据集[7]的平均估计误差列于本表中。

5.4 与当前最先进的比较
5.4.1 在MSRA数据集上比较
在MSRA数据集上,我们将基于3D CNN的手姿态估计方法与七种最先进的方法进行比较:层次回归方法[26],联合矩阵分解和完成(JMFC)方法[69],基于CNN的多视图方法[19],基于局部表面法线(LSN)的方法[45],使用深度生成模型的交叉网络[23],具有手姿势先验和改进的改良2D CNN(DeepPrior++)[70],区域集合网络(REN)[72]和姿势引导结构化REN(Pose-REN)[71]。注意,由于层次回归方法[26]已经证明优于[1],[6]中的方法,我们间接地将我们的方法与[1],[6]进行了比较。
如图10所示,我们的基于3D CNN的方法在MSRA数据集上优于最先进的方法。不同错误阈值的好帧比例如图10(左)所示。当误差阈值大于10mm时,我们的方法可以获得最佳性能。例如,当误差阈值为30mm时,我们方法的好帧比例比[71],[70],[19],[23],[45](手指联合回归),[26]和[69]中的方法分别高约6%,10%,20%,22%,28%,33%和39%。当误差阈值为5mm时,我们方法中良好帧的比例略差于[26]和[69]中的方法。这可能是由体素的相对较大的边缘长度引起的,当体积分辨率为32×32×32时,平均为5.5mm。在图10(中间和右侧)中,我们与[19],[26],[71],[72]中的方法比较不同偏航和俯仰角度的平均误差距离。可以看出,我们方法中不同视角的平均误差比[26],[19],[72]和[71]中的方法分别小约7mm,4.5mm,1.8mm和0.8mm。我们的方法与俯仰角度变化的差异较小,标准偏差(0.58mm)小于[26]中的方法(0.79mm),[19](0.64mm),[72](0.82mm)和[71](0.63毫米)。

图10:与最先进的方法[19],[23],[26],[45],[69],[70],[71],[72]在MSRA数据集上的比[较26]]。左:好帧的比例超过不同的误差阈值。中间和右侧:相对于相机框架的不同偏航和俯仰视角的平均误差距离。
5.4.2 在NYU数据集上比较
在NYU手姿势数据集上,我们首先将我们基于3D CNN的手部姿势估计方法与九种最先进的方法进行比较:基于2D CNN的热图回归方法[7],基于2D CNN的直接回归具有姿势先验的方法(DeepPrior)[17],基于2D CNN的方法使用反馈回路[18],基于2D CNN的手模型参数回归方法[22],基于深度特征的矩阵完成方法(DeepHand)[20],交叉网使用深度生成模型[23],Lie-X方法应用李群理论[73],DeepPrior++方法[70]和Pose-REN方法[71]。对于基于2D CNN的热图回归方法[7],我们使用热图估计2D关节位置,并使用相应的深度值将它们转换为3D位置。如图11(左)所示,我们的方法在所有错误阈值上优于这九种方法。例如,当误差阈值在20mm和50mm之间时,我们方法的好帧的比例比Pose-REN方法[71]的大约多10%。
为了与[21]中基于空间注意网络的分层混合方法进行公平比较,我们在[21]中的实验中评估了11个手关节子集(去除除拇指的根关节外的手掌关节)中不同误差阈值内关节的比例。如图11(中)所示,我们的方法优于[17],[18],[21],[70],[71]中的方法,在所有误差阈值中。例如,我们方法误差阈值20mm内的关节比例比[21]中方法的约20%多。
我们还将我们的方法的平均误差距离与[18],[22],[70],[71]中的方法进行了比较。如图11(右)所示,我们的方法在大多数关节上实现了最小的平均误差距离,并且我们方法中所有关节的平均误差距离比方法[18],[22],[70]和[71]分别小约5.5mm,6.5mm,2mm和1.5mm。
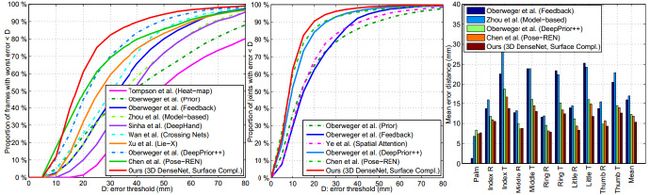
图11:与最先进的方法[7],[17],[18],[20],[21],[22],[23],[70],[71]的比较,[73]关于纽约大学数据集[7]。左:好帧的比例超过不同的误差阈值。中:关节在不同误差阈值内的比例。右:每个关节的平均误差距离(R:root,T:tip)。
5.4.3 在ICVL数据集上比较
在ICVL手姿势数据集上,我们将基于3D CNN的手姿态估计方法与八种最先进的方法进行比较:潜在回归森林(LRF)[8],层次回归方法[26],手模型基于参数的方法[22],LSN方法[45],交叉网使用深度生成模型[23],REN方法[24],DeepPrior++方法[70]和Pose-REN方法[71]。如图12(左)所示,我们的方法在此数据集的大多数错误阈值上优于这八种方法。
我们还将我们的方法的平均误差距离与[17],[45],[71],[72]中的方法进行了比较。如图12(右)所示,我们的方法在大多数关节上实现了最小的平均误差距离。我们方法的所有关节的平均误差距离为6.7mm,而[17],[45],[72]和[71]中的方法的平均误差距离为9.3mm,8.2mm,7.3mm和6.8mm。
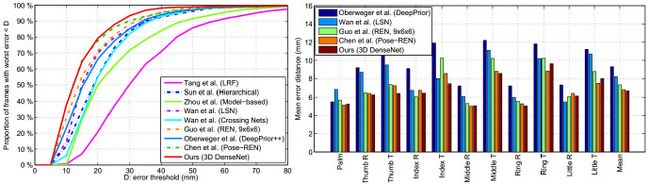
图12:与ICVL数据集[8],[22],[23],[26],[45],[70],[71],[72]的最新方法[8]进行比较[8]]。左:好帧的比例超过不同的误差阈值。右:每个关节的平均误差距离(R:root,T:tip)。
5.5 交叉数据集实验
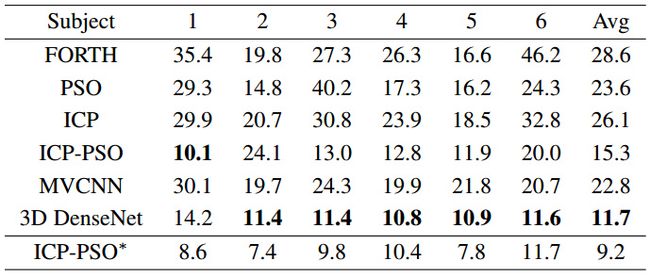
为了评估基于3D CNN的手姿态估计方法的泛化能力,我们进行了交叉数据集实验,其中3D CNN模型在整个MSRA数据集上进行训练[26],并在[34]中发布的整个数据集上进行评估。根据[34]中的评估指标,我们计算了手腕和五指尖的平均误差距离。如表2所示,我们将基于3D CNN的方法与[34]中报告的基于模型的跟踪方法进行了比较,这些方法是FORTH [5],PSO [34],ICP [74],ICP-PSO[34]和ICP-PSO*(基于手指初始化的ICP-PSO)[34],以及基于CNN的多视图方法[19]。可以看出,我们的方法在三个受试者和所有受试者的平均误差上实现了第二好的结果。
值得注意的是,[34]中基于模型的方法需要为每个受试者精心校准的手模型。然而,我们的方法不使用校准的手模型,因此对于不同的受试者更灵活。在这种情况下,我们的方法仍然优于FORTH,PSO,ICP和ICP-PSO方法,如表2所示。我们的方法比使用真实值初始化第一帧的ICP-PSO*方法稍微差一点。但是我们的方法不使用测试数据的任何真实值,而是在更具挑战性的跨数据集上执行。因此,我们的方法在该交叉数据集实验中获得的总体第二好结果表明我们的基于3D CNN的方法具有良好的泛化能力。
表2:在[34]中发布的数据集上测试的7种方法的6名受试者的平均估计误差(以mm为单位)。
5.6 定性分析结果
MSRA,NYU和ICVL数据集的一些定性结果如图13所示。我们将3D深度密集网络与2D深度密集网络的基线方法进行比较,如第5.3.4节所述。如图13中可见,当使用相同的残差网络架构时,我们的基于3D CNN的方法可以比基于2D CNN的方法更好地利用深度信息并提供更准确的估计。
我们还与英特尔RealSense SDK进行定性比较[32]。我们在整个MSRA数据集上训练3D CNN模型,并应用此预训练的3D CNN模型,在真实场景中使用英特尔实感SR300深度相机进行实时手姿态估计。我们基于3D CNN的方法和英特尔实感SDK[32]的定性结果如图14所示。可以看出,英特尔实感SDK不像我们的方法那样准确地适应复杂的手部姿势。例如,在图14的第4列中,当小指被无名指遮挡时,英特尔实感SDK会错误估计无名指的位置;在图14的第6列中,英特尔实感SDK将食指与中指混淆;在图14的第2列,第8列和第9列中,英特尔实感SDK将无名指与小手指混淆。相比之下,从可以更好地利用3D信息的3D CNN中获益,我们的方法能够正确估计这些情况下的手部姿势。我们的演示视频中提供了更多比较,可在线获取。

图13:MSRA,NYU和ICVL数据集的定性结果。我们将基于3D深密网络(每个数据集的第2列)的方法与基于2D深密网络的方法(每个数据集的第1列)进行比较。在每个数据集的最后一列中显示了真实的手关节位置。我们用点云显示手部关节位置和骨骼。使用不同颜色可视化不同的手关节和骨骼。这个图片最好用彩色看。

图14:使用英特尔实感SR300深度相机在实际场景中进行测试的定性结果。对于每个手姿势,第1行显示手的RGB图像;第2行显示手的深度图像;第3行显示英特尔实感SDK估计的手势[32];第4行显示我们基于3D CNN的方法估计的手姿势。我们用点云显示手部关节位置和骨骼。拇指,食指,中指,无名和小指的关节分别以绿色,蓝色,青色,黄色和粉红色可视化。 这个图片最好用彩色看。
5.7 运行时间和模型大小
基于3D CNN的手姿态估计方法的运行时间在5.2节中描述的计算机上平均为7.9ms。在GPU上生成具有32×32×32体积分辨率的投影D-TSDF体积的过程平均需要2.9ms。在GPU上运行的3D深度密集网络前向传播的过程平均需要4.5ms。从3D CNN输出的PCA系数重建3D体积中的手关节的3D坐标并将其转换为摄像机坐标系中的3D位置的过程在CPU上平均需要0.5ms。因此,我们的方法能够以超过126帧/秒(fps)的速度实时运行。在我们的方法中采用手表面补全步骤时,3D U-Net和3D深密网络前向传播平均需要7.6ms。因此,使用手表面补全的方法的运行时间是11.0ms,帧速率是91fps。
对于模型尺寸,我们的3D深度密集网络模型大约需要192MB,用于手部表面完成的3D U-Net大约需要200MB,而[19]中的多视图CNN大约需要1.2GB。网络参数以32位浮点存储。
6 结论
我们提出了一种新的基于3D CNN的手姿态估计方法。通过采用投影D-TSDF,我们将手部深度图像编码为3D体积表示,然后将其馈送到3D CNN。我们展示了3D CNN在单通道中将3D体积映射到3D关节位置很容易以端到端的方式进行训练。3D深度密集网络可以进一步提高3D手部姿势估计的学习能力。为了使3D CNN对各种手部大小和全局方向具有鲁棒性,我们对训练数据执行3D数据增强。为了解决自我遮挡问题,我们利用完整的手部表面作为学习3D手姿势的中间监督。实验结果表明,我们提出的基于3D CNN的方法在三个具有挑战性的数据集上实现了3D手姿态估计的最先进性能,并且能够以良好的泛化能力实时运行。