理解卷积 Convolution

http://www.qiujiawei.com/convolution/

数学中的卷积

卷积的wiki：Convolution。

卷积和(convolution sum)的公式是:

y(t)=x(t)∗h(t)=∑τ=−∞∞x(τ)h(t−τ) y(t)=x(t)∗h(t)=∑τ=−∞∞x(τ)h(t−τ)

写成积分形式是:

x(t)∗h(t)=∫∞−∞x(τ)h(t−τ)dτ=∫∞−∞x(t−τ)h(τ)dτ x(t)∗h(t)=∫−∞∞x(τ)h(t−τ)dτ=∫−∞∞x(t−τ)h(τ)dτ

要理解这个东西，比较难，一种是公式推导，不过是从傅里叶变换得到的；一种是用狄拉克δ函数来辅助理解（我自认为的）；最后一种是通过线性时不变系统理论LTI system theory。

先讲第一种吧。

第一种思路：傅里叶变换与卷积

首先要搬出傅里叶变换的一个推论：

F[αf(t)+βg(t)]=αF(s)+βG(s) F[αf(t)+βg(t)]=αF(s)+βG(s)

这个公式意思是，一个时域下的复杂信号函数可以分解成多个简单信号函数的和，然后对各个子信号函数做傅里叶变换并再次求和，就求出了原信号的傅里叶变换。这个事实显然很有用处。

但除了加法之外，还有乘法。这时候有一个问题：是否存在某种新的f(t)和g(t)的结合方式，使得f(t)和g(t)结合后的函数的傅里叶变换结果是F(s)G(s)？

要求这个问题的解，要用倒推法。

首先，设有信号函数f(x)和g(t)（注意，x、t都是指横轴变量，只是用来区分开f和g），G(s)、F(s)分别是f(x)和g(t)的傅里叶变换，于是有:

G(s)F(s)=∫∞−∞e−2πistg(t)dt∫∞−∞e−2πisxf(x)dx G(s)F(s)=∫−∞∞e−2πistg(t)dt∫−∞∞e−2πisxf(x)dx

接着做一些变换:

∫∞−∞e−2πistg(t)dt∫∞−∞e−2πisxf(x)dx=∫∞−∞∫∞−∞e−2πiste−2πisxg(t)f(x)dtdx ∫−∞∞e−2πistg(t)dt∫−∞∞e−2πisxf(x)dx=∫−∞∞∫−∞∞e−2πiste−2πisxg(t)f(x)dtdx

=∫∞−∞∫∞−∞e−2πis(t+x)g(t)f(x)dtdx =∫−∞∞∫−∞∞e−2πis(t+x)g(t)f(x)dtdx

=∫∞−∞(∫∞−∞e−2πis(t+x)g(t)dt)f(x)dx =∫−∞∞(∫−∞∞e−2πis(t+x)g(t)dt)f(x)dx

现在设u = t + x，所以t = u - x，du = dt（这是把x看做常数项了）。则有：

∫∞−∞(∫∞−∞e−2πis(t+x)g(t)dt)f(x)dx=∫∞−∞(∫∞−∞e−2πisug(u−x)du)f(x)dx ∫−∞∞(∫−∞∞e−2πis(t+x)g(t)dt)f(x)dx=∫−∞∞(∫−∞∞e−2πisug(u−x)du)f(x)dx

接着调整下积分顺序：

∫∞−∞(∫∞−∞e−2πisug(u−x)du)f(x)dx=∫∞−∞∫∞−∞e−2πisug(u−x)f(x)dudx ∫−∞∞(∫−∞∞e−2πisug(u−x)du)f(x)dx=∫−∞∞∫−∞∞e−2πisug(u−x)f(x)dudx

=∫∞−∞∫∞−∞e−2πisug(u−x)f(x)dxdu =∫−∞∞∫−∞∞e−2πisug(u−x)f(x)dxdu

=∫∞−∞e−2πisu(∫∞−∞g(u−x)f(x)dx)du =∫−∞∞e−2πisu(∫−∞∞g(u−x)f(x)dx)du

括号内那个积分是一个关于u的函数，所以可以设成h(u)：

h(u)=∫∞−∞g(u−x)f(x)dx h(u)=∫−∞∞g(u−x)f(x)dx

于是上面的式子就变成:

∫∞−∞e−2πisu(∫∞−∞g(u−x)f(x)dx)du=∫∞−∞e−2πisuh(u)du=F[h(s)]=H(s) ∫−∞∞e−2πisu(∫−∞∞g(u−x)f(x)dx)du=∫−∞∞e−2πisuh(u)du=F[h(s)]=H(s)

这个结论，可以简化成：

H(s)=G(s)F(s) H(s)=G(s)F(s)

再来看下h(u)。如果把h(u)的u换成t（这是可以的，只是一个符号而已），就有:

h(t)=∫∞−∞g(t−x)f(x)dx h(t)=∫−∞∞g(t−x)f(x)dx

2个终极公式都出来了。

最后，我们还要定义一个特殊的二元运算符号 ∗ ∗来替代h(t)（也叫卷积运算符，注意，这个不是乘法的乘号哦）：

h(t)=(g∗f)(t)=∫∞−∞g(t−x)f(x)dx h(t)=(g∗f)(t)=∫−∞∞g(t−x)f(x)dx

于是有：

H(s)=G(s)F(s) H(s)=G(s)F(s)

F[h(t)]=F[g(s)]F[f(s)] F[h(t)]=F[g(s)]F[f(s)]

F[(g∗f)(s)]=F[g(s)]F[f(s)] F[(g∗f)(s)]=F[g(s)]F[f(s)]

最后的公式，也被叫做卷积定理(Convolution Theorem)。

这个定理说明，信号f和信号g的卷积的傅里叶变换，等于f、g各自的傅里叶变换的积。

第二种思路：狄拉克δ函数与卷积

第二种思路的关键在于狄拉克δ函数。

狄拉克δ函数 dirac delta function

狄拉克δ函数的wiki：dirac delta function。

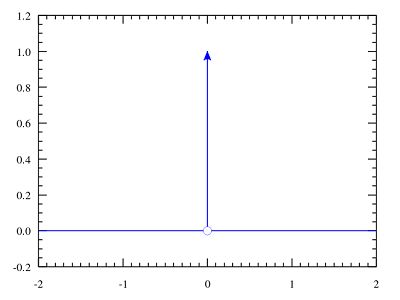
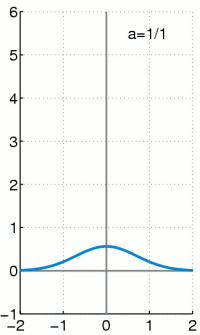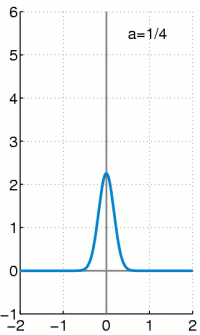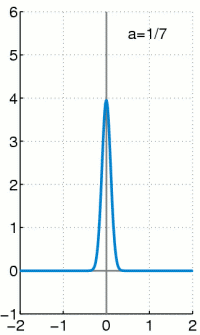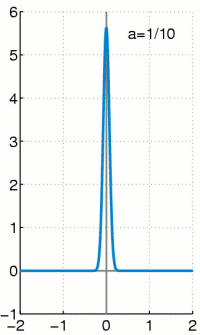
狄拉克δ函数在坐标系上的长相:

（图片来自wiki）

在信号处理科学中狄拉克δ函数被称为单位脉冲信号(unit impulse symbol）。上面这个图也很形象地说明了这一点。

狄拉克δ函数有这样的性质:

delta(t)={+∞,t=00,t≠0 delta(t)={+∞,t=00,t≠0

∫∞−∞δ(t)dt=1 ∫−∞∞δ(t)dt=1

狄拉克δ函数在t等于0时值为正无穷，t不等于0时则为0，且在整个定义域的积分等于1。

狄拉克δ函数与卷积

考虑卷积公式的一个特殊情况：当h(t)是狄拉克δ函数时。现在试一下把h(t)代入卷积公式，得到:

x(t)∗h(t)=x(t)∗δ(t)=∫∞−∞x(τ)δ(t−τ)dτ=x(t) x(t)∗h(t)=x(t)∗δ(t)=∫−∞∞x(τ)δ(t−τ)dτ=x(t)

(最后一步跳跃得比较厉害，后文会有说明）

这个结果说明，x(t)和狄拉克δ函数卷积的结果还是x(t)，为什么会这样呢？

再看下前面给出的卷积和标准公式：

y(t)=x(t)∗h(t)=∑τ=−∞∞x(τ)h(t−τ) y(t)=x(t)∗h(t)=∑τ=−∞∞x(τ)h(t−τ)

把其中的 h(t−τ) h(t−τ)换成 δ(t−τ) δ(t−τ)，那么里面的 t−τ t−τ，其实就是让那个脉冲信号在横轴上移动(偏移) τ τ距离。根据狄拉克δ函数的定义，可以知道，当 t=τ t=τ时， x(τ)h(t−τ) x(τ)h(t−τ)才非0，且等于 x(τ) x(τ)。所以卷积和也就等于 x(τ) x(τ)。（这也算是上面的公式的证明吧）

将这个特殊情况一般化，即不限制h = δ时，就是所谓的卷积公式了。

第三种思路：线性时不变系统·理论 LTI system theory

这个还没搞懂，搞懂了再来填坑

二维卷积以及图像中的卷积

上面讨论的仅仅是一维的卷积。幸运的是，高维卷积可以简单地根据一维卷积得到，比如说二维的卷积：

f(x,y)∗g(x,y)=∑x′∑y′f(x′,y′)g(x−x′,y−y′) f(x,y)∗g(x,y)=∑x′∑y′f(x′,y′)g(x−x′,y−y′)

积分形式是：

(f∗g)(x,y)=∫∫f(x′,y′)g(x−x′,y−y′)dx′dy′ (f∗g)(x,y)=∫∫f(x′,y′)g(x−x′,y−y′)dx′dy′

如果给定一个范围r，则有：

f(x,y)∗g(x,y)=∑x′=−rx′=r∑y′=−ry′=rf(x′,y′)g(x−x′,y−y′) f(x,y)∗g(x,y)=∑x′=−rx′=r∑y′=−ry′=rf(x′,y′)g(x−x′,y−y′)

现在想象一下，把一幅图片(位图)当做是一个函数：

f(x,y)=RGB value f(x,y)=RGB value

先让自己对这个式子有一个几何空间上的想象：带有2个变量的函数，它的几何表示是三维的，三个坐标轴分别是：x、y、f(x,y)，所以f(x,y)表示的是三维空间里的一个连续表面(surface)。

然后，我们再来回顾下线性代数——矩阵。假设我们有一个128X128的bmp图像，可以用一个矩阵A(应该说是方阵)来表示它，A的每一个元素是一个rgb值。 有了这个图像->矩阵的转换关系后，我们就可以用线性代数的知识对这个图像做处理。

比如说，我们用矩阵乘法吧。假设有另一个和A同阶的方阵S，很显然，下面的等式成立：

AS=A′ AS=A′

这个式子意味着，图像处理可以抽象成矩阵的线性运算。比如当S是单位矩阵I时，显然有 AI=A AI=A，即A保持不变，什么都没做。

好了，明确了图像可以用线性代数的方法来加工处理后，要理解图像卷积就简单了。

上面说的‘转换’方阵S，是和A同阶的方阵。这个‘同阶’性质，是不是必要的？其实不是。只要你有办法使得A变成A'，就可以了。中间的S，代表的是一个转换过程。

卷积转换，是一个特殊的转换，首先，它有一个叫做窗口的东西（或者叫卷积子），一般情况下这个窗口是一个比A的阶数小得多的方阵。

如果拿这个小方阵R去和A的局部区域做线性变换(更具体地说，是点积运算)，则有：

Ax,y,w,h⋅Rw,h=∑x′=x−w/2x′=x+w/2∑y′=y−h/2y′=y+h/2A[x′,y′]R[x′−x,y′−y]=new RGB value Ax,y,w,h⋅Rw,h=∑x′=x−w/2x′=x+w/2∑y′=y−h/2y′=y+h/2A[x′,y′]R[x′−x,y′−y]=new RGB value

把得到的这个RGB值赋给A[x,y]，就有：

A[x,y]R=A′[x,y] A[x,y]R=A′[x,y]

简单地说就是，A[x,y]的值被R刷新了。如果对整幅图像的每一个像素都和R做一次点积运算，整幅图像就被刷新了。

这就是图像的卷积变换的本质。

找到的相关资料

The Convolution Sum for Discrete-Time LTI Systems. Andrew W. H. House

Written on October 18, 2015